Константан — термостабильный сплав

Прайс-лист с актуальными ценами на лето 2021г.

Вольфрамовая проволока ВА 0,08 – 0.8 мм		6580
Проволока хромель НХ9,5 диаметры 0,2 – 3,2 мм	Проволока термопарная для изготовления термопар и компенационных проводов. Класс точности А1 и А2	4200
Молибденовая проволока 0,4мм – 3,17 мм	Молибденовая проволока МЧ 2,0мм, ГОСТ 27266-87, Проволока из марки молибдена МЧ	5760
Молибденовый пруток	Прутки молибденовые, молибденовый пруток МЧ и МЧВП (ТУ 48-19-247-93)	5160
Проволока никелевая НП2 0,1 – 3,0 мм	Никелевая проволока ДКРНМ 0,6 КТ НП2, НП1 ДКРНТ 0,1мм	4200
Плита монель 400	Плита монель 400, Лист монель, MONEL400, 401, 404, R-405, K-500, Монель НМЖМц 28-2,5-1,5, НМЖМц 28-2,5-1,5	4200
Никелевый пруток НП2 ф 7-20 мм	Пруток ДКРНТ 8,0-20 НП2, Пруток ДКРНТ 8,0-20 НП2, ГОСТ 13083-77	3600
Лента константан МНМц40-1,5	Лента константан МНМц40-1,5 0,2х250мм. ГОСТ 5189-75	3960
Никелевый прокат	Проволока никелевая НП2, Пруток (круг) никелевый 10мм, Лист Лента никелевая	4200
Проволока нихром Х20Н80	Нихромовая проволока Х20Н80, ГОСТ 8803-89	2360
Проволока алюмель НМЦАк 2-2-1 Ф 0,2 – 3,2 мм	Проволока термопарная алюмель НМЦАК 2-2-1	4200
Пруток монель НМЖМЦ 28-25-1,5	Монелевый пруток (круг) НМЖМц 28-2,5-1,5 диаметр от 14 до 100мм	3600
Проволока константан МНМЦ40-1,5 ф 0,05-3,0 мм	Константановая проволока 0,1мм – 3,0мм	3240
Лист монель 400 2х600х1500 мм	Монелевый лист, лист монель 400 2х600х1500мм	3960
Лента нихром Х20Н80		2400
Проволока нихром Х15Н60		1920
Вольфрамовые прутки (электроды) ВЛ, СВИ, ВА	Прутки ВЛ, СВИ (электроды) диаметр 1,0 – 8,0мм	7200
Лист монель 400 4х1200х1500 мм		4800
Плита монель 400 20х600х1500 мм		3960
Плита монель 400 16х600х1500 мм		3960
Проволока монель НМЖМц 28-2,5-1,5 0,3 мм 0,5 мм		2880
Круг мельхиор МНЖМц30-1-1 200 мм		1620
Труба монель 400 16х2х2000 мм		5580
Труба мельхиор МНЖМц 30-1-1 16х2х2000 мм		2600
Пруток мельхиор МН19ВИ 14 мм		4200
Проволока термопарная копель МНМц 43-0,5		3600

Главная » Продукция » Константан

Свойства меди

Востребованность меди в электротехнике обусловлена следующими положительными качествами:

1. высокая электропроводимость;
2. пластичность. Из меди делают тончайшие жилы и пластины с толщиной, исчисляемой микронами. Благодаря пластичности, она не обламывается при монтаже, выдерживая множество циклов сгибания-разгибания без развития усталостных явлений;
3. распространенность и простота добычи. Это преимущество условно. Получение меди обходится дешевле серебра — единственного металла, превосходящего ее в электропроводимости. Но в сравнении с алюминием, а тем более со сталью, медь стоит гораздо дороже. Потому ее нередко заменяют этими материалами;
4. антикоррозионные свойства;
5. прочность. Благодаря ей, изделия из меди устойчивы к деформациям.
6. материал легко поддается пайке и сварке.

Источником меди служит сульфидная руда. Для применения в электротехнике металл после плавки руды подвергают электролитической очистке, так что доля примесей в нем составляет 0,05-0,1% (высококачественная рафинированная медь марок М0 и М1, также называемая электролитической).

В процессе получения минимизируют воздействие кислорода на металл, иначе механические характеристики последнего ухудшаются.

Сульфидная руда

Дешевле меди стоят сплавы на ее основе — латунь (с цинком) и бронза (с оловом или свинцом). Помимо олова или свинца, в бронзу могут добавлять бериллий (бериллиевая бронза), кадмий, кремний, фосфор, магний, хром.

Сплавы превосходят чистую медь в прочности, но уступают ей в проводимости.

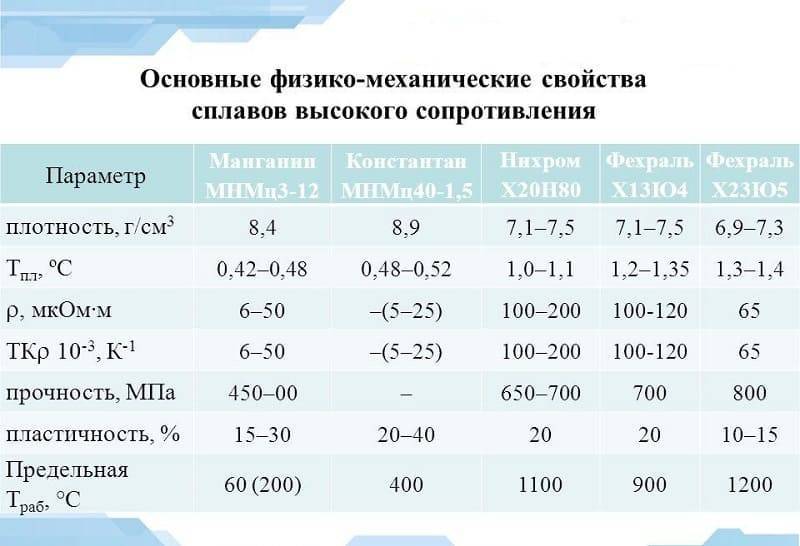
Свойства, характеристики константановой проволоки

Свойства константановой проволоки обусловлены способами обработки сплава, которые могут производиться давлением или отжигом, выполняемым при высоких температурных режимах. Прочность сплава регулируется нормативными документами, находится в пределах 650-720 МПа для твердых материалов и 400-500 МПа – для мягких. Предел прочности на разрыв термически не обработанной константановой проволоки – довольно небольшой – всего 400 Мпа, но уже после низкотемпературного отжига данный показатель значительно увеличивается, и становится практически таким же, как у стали 45.

Среди основных свойств константановой проволоки можно выделить:

• прочность;
• жаростойкость;
• устойчивость к процессам коррозии;
• высокое электрическое сопротивление.

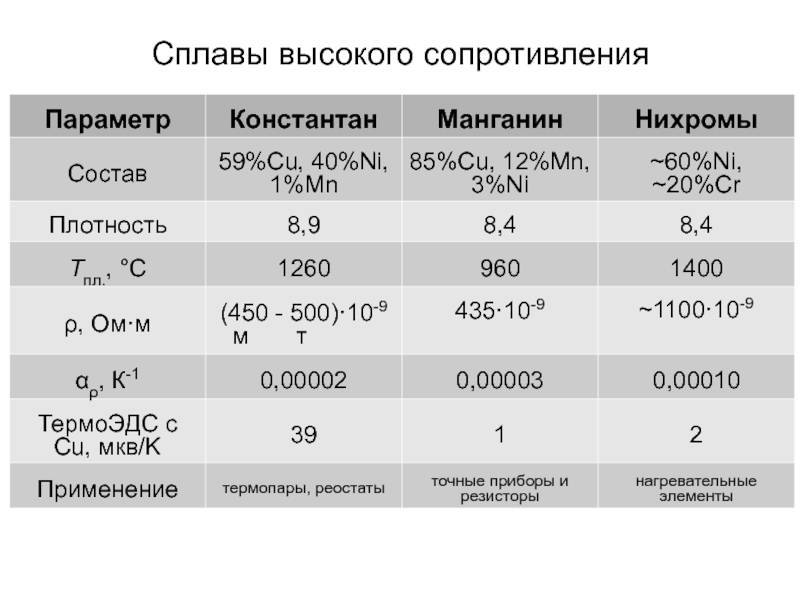
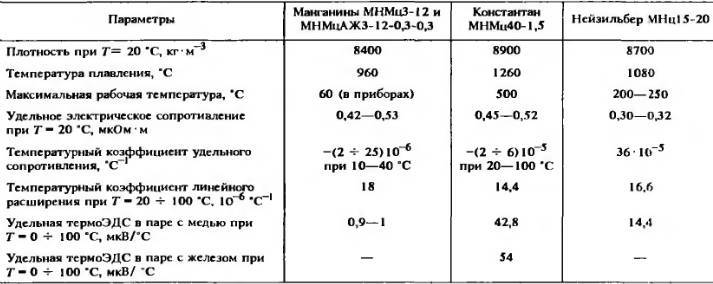
Характеристики изделия зависят от свойств константана. Наибольшее распространение получила марка изделия МНМц40-1,5. Эта продукция, представляющая собой сплав серебристого цвета с желтоватым отливом, содержит около 56,2% меди по массе, 39-41% кобальта и никеля в общем массе, и марганец (1-2%). Кроме этого, возможно содержание примесей, но в ограниченном количестве

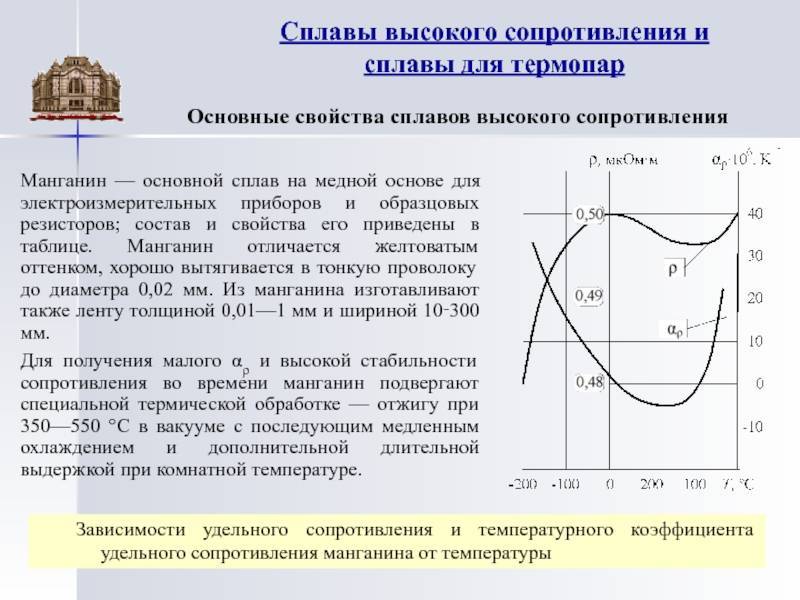
Сплав характеризуется высоким показателем удельного электрического сопротивления (от 0,45 до 0,52 мкОм*м), и, что важно, – сохраняет его при повышении температуры до 400-500оС

Плотность константановой проволоки зависит от марки – варьируется в пределах интервала 8800 – 8900 кг/м3. Проволока константановая не магнитна.

Особого внимания требует термоэлектродвижущая сила константана (ТЭДС), которая является высокой в совокупности с такими элементами, как медь, железо, хромель – (хромоникелевый сплав), обеспечивая применение полуфабриката для производства термопар. При кратковременном нагреве до температуры 900оС, на поверхности создается изолирующий слой оксидной плёнки. Это исключает выполнение дополнительных операций в технологическом процессе по покрытию проволоки лаком или другим изолирующим слоем, благодаря чему снижается стоимость продукции.

Сплав обладает хорошей обрабатываемостью. Относительное сужение константановой проволоки может доходить до 71%, а удлинение – до 30%.  Благодаря пластичности изделия МНМц40-1,5 обеспечивается производство из него тонкой проволоки, сечением до микронного диаметра. Материал легко соединяется путем сварки, пайки.

Содержание в составе константановой проволоки таких элементов, как никель, медь, придают данной продукции высокую устойчивость к воздействию процессов коррозии. При температуре менее 800 °С продукция не окисляется под воздействием кислорода. Прекрасно противостоит воздействию большинства кислот органического происхождения, растворов солей.

Поставляется константановая проволока в катушках, мотках, бухтах. Твердые изделия выпускаются диаметром 0,02-5 мм, мягкие – 0,1-5 миллиметров. Пластические свойства мягкой константановой проволоки выше. Контроль качества производства полуфабрикатов осуществляется на всех этапах технологического процесса. Поверхность материала контролируется ГОСТ(ом), не допуская механических повреждений, расслоений и надрывов.

Константановая проволока с сечением меньше 0,1 мм часто носит название «константановая нить» или в обиходе «проволока микронных размеров». У нас можно купить константановую проволоку и константановую нить.

Как и вся металлопродукция, константановая проволока имеет свои преимущества и недостатки.

Среди достоинств можно выделить:

• высокие технологические характеристики (обрабатываемость и пр.);
• хорошее электросопротивление;
• термостабильность;
• в паре с некоторыми сплавами, металлами – высокое значение ТЭДС;
• низкий температурный коэффициент электросопротивления.

Недостаток – относительно низкая температура перехода в жидкое состояние.

Сопротивление провода

Величина сопротивления провода зависит от трех параметров: удельного сопротивления металла, длины и диаметра самого провода. Формула для расчета сопротивления провода:

где: R — сопротивление провода (Ом) ρ — удельное сопротивление металла (Ом.m) L — длина провода (м) А — площадь поперечного сечения провода (м2)

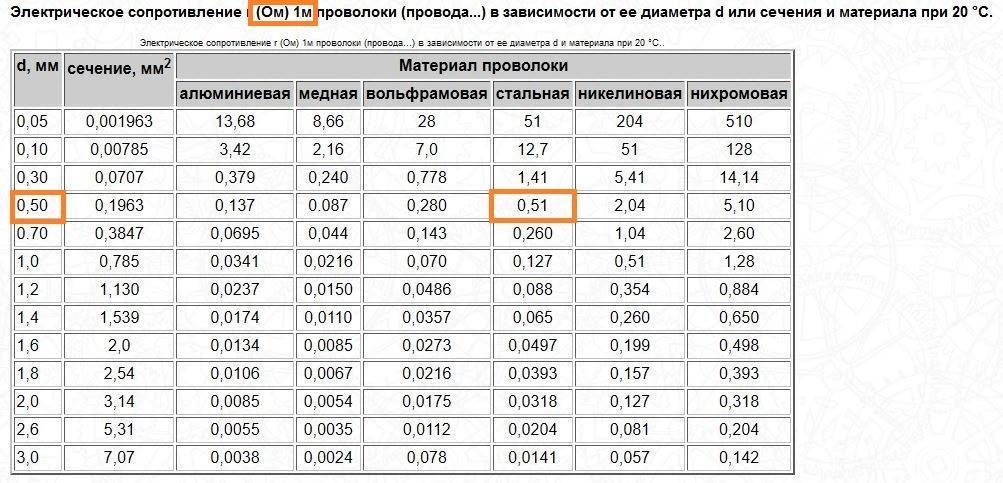
В качестве примера рассмотрим проволочный резистор из нихрома с удельным сопротивлением 1.10×10-6 Ом.м. Проволока имеет длину 1500 мм и диаметр 0,5 мм. На основе этих трех параметров рассчитаем сопротивление провода из нихрома:

R=1,1*10 -6 *(1,5/0,000000196) = 8,4 Ом

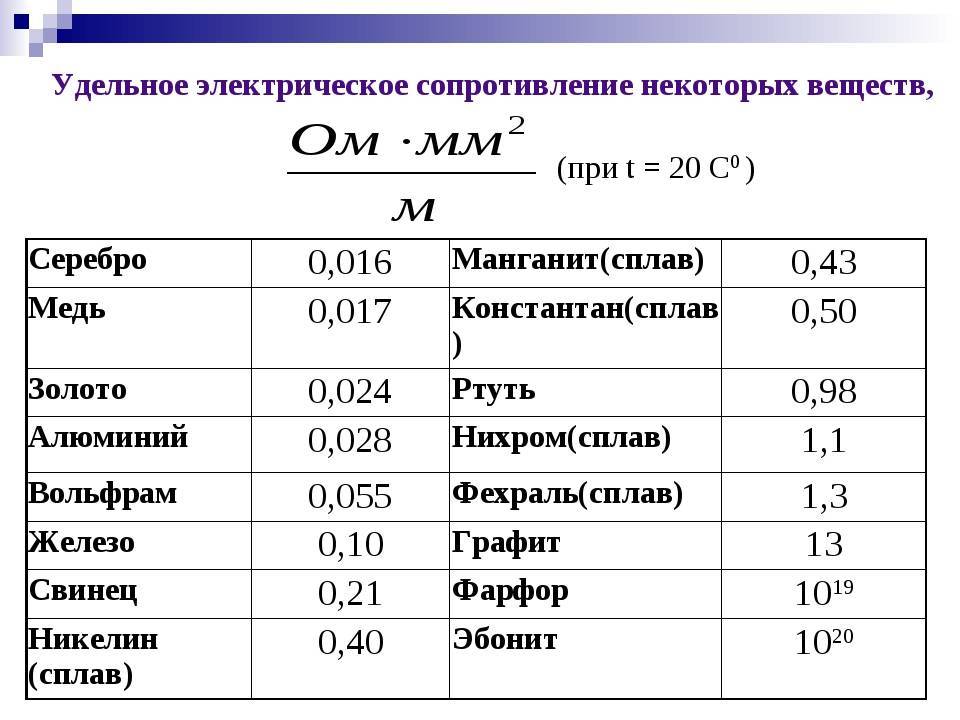
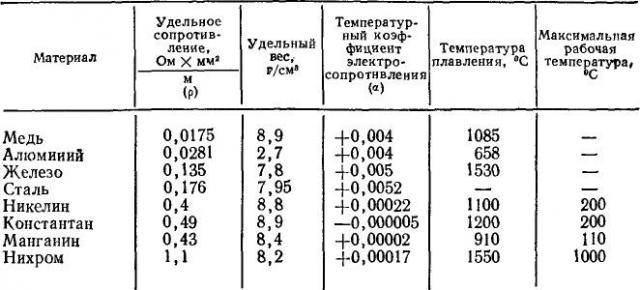
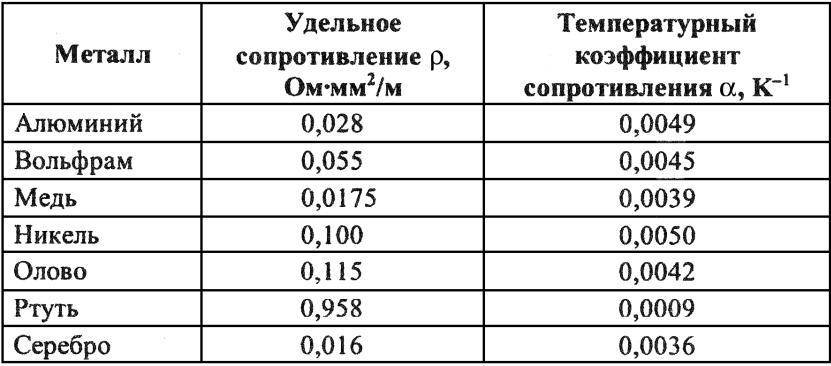
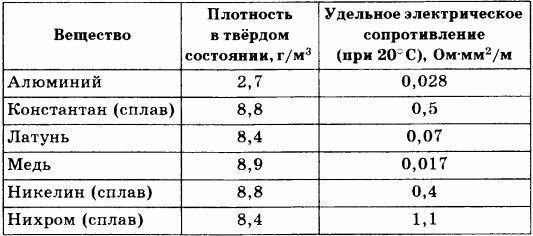
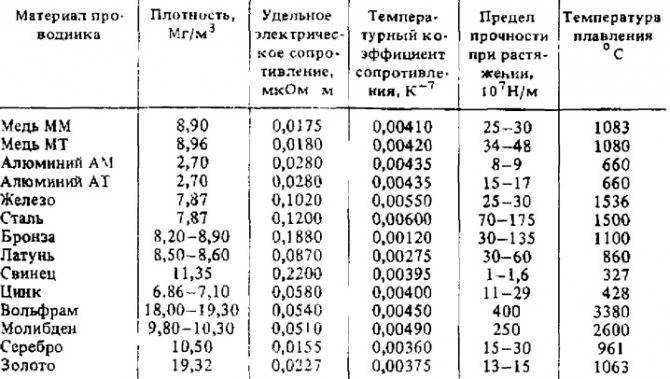
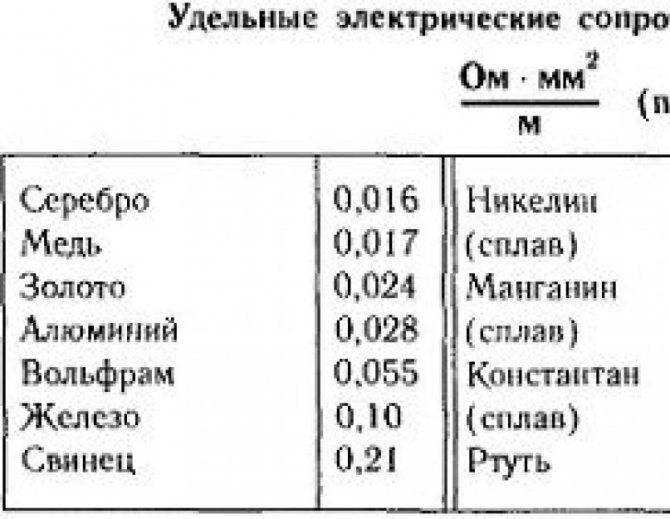
Нихром и константан часто используют в качестве материала для сопротивлений. Ниже в таблице вы можете посмотреть удельное сопротивление некоторых наиболее часто используемых металлов.

Теплопроводность цветных металлов, теплоемкость и плотность сплавов

В таблице представлены значения теплопроводности металлов (цветных), а также химический состав металлов и технических сплавов в интервале температуры от 0 до 600°С.

Цветные металлы и сплавы: никель Ni, монель, нихром; сплавы никеля (по ГОСТ 492-58): мельхиор НМ81, НМ70, константан НММц 58,5-1,54, копель НМ 56,5, монель НМЖМц и К-монель, алюмель, хромель, манганин НММц 85-12, инвар; магниевые сплавы (по ГОСТ 2856-68), электрон, платинородий; мягкие припои (по ГОСТ 1499-70): олово чистое, свинец, ПОС-90, ПОС-40, ПОС-30, сплав Розе, сплав Вуда.

По данным таблицы видно, что высокую теплопроводность (при комнатной температуре) имеют магниевые сплавы и никель. Низкая же теплопроводность свойственна нихрому, инвару и сплаву Вуда.

Коэффициенты теплопроводности алюминиевых, медных и никелевых сплавов

Теплопроводность металлов, алюминиевых, медных и никелевых сплавов в таблице дана в интервале температуры от 0 до 600°С в размерности Вт/(м·град).Металлы и сплавы: алюминий, алюминиевые сплавы, дюралюминий, латунь, медь, монель, нейзильбер, нихром, нихром железистый, сталь мягкая. Алюминиевые сплавы имеют большую теплопроводность, чем латунь и сплавы никеля.

Коэффициенты теплопроводности сплавов

В таблице даны значения теплопроводности сплавов в интервале температуры от 20 до 200ºС.Сплавы: алюминиевая бронза, бронза, бронза фосфористая, инвар, константан, манганин, магниевые сплавы, медные сплавы, сплав Розе, сплав Вуда, никелевые сплавы, никелевое серебро, платиноиридий, сплав электрон, платинородий.

В таблице указаны значения удельного электрического сопротивления и КТР металлической проволоки, выполненной из различных металлов и сплавов.

Материал проволоки: алюминий, вольфрам, железо, золото, латунь, манганин, медь, никель, константан, нихром, олово, платина, свинец, серебро, цинк.

Как видно из таблицы, нихромовая проволока имеет высокое удельное электрическое сопротивление и успешно применяется в качестве спиралей накаливания нагревательных элементов множества бытовых и промышленных устройств.

Удельная теплоемкость цветных сплавов

В таблице приведены величины удельной (массовой) теплоемкости двухкомпонентных и многокомпонентных цветных сплавов, не содержащих железа, при температуре от 123 до 1000К. Теплоемкость указана в размерности кДж/(кг·град).

Дана теплоемкость следующих сплавов: сплавы, содержащие алюминий, медь, магний, ванадий, цинк, висмут, золото, свинец, олово, кадмий, никель, иридий, платина, калий, натрий, марганец, титан, сплав висмут — свинец — олово, сплав висмут-свинец, висмут — свинец — кадмий, алюмель, сплав липовица, нихром, сплав розе.

Также существует отдельная таблица, где представлена удельная теплоемкость металлов при различных температурах.

Удельная теплоемкость многокомпонентных специальных сплавов

Удельная (массовая) теплоемкость многокомпонентных специальных сплавов приведена в таблице при температуре от 0 до 1300ºС. Размерность теплоемкости кал/(г·град).Теплоемкость специальных сплавов: алюмель, белл-металл, сплав Вуда, инвар, липовица сплав, манганин, монель, сплав Розе, фосфористая бронза, хромель, сплав Na-K, сплав Pb — Bi, Pb — Bi — Sn, Zn — Sn — Ni — Fe — Mn.

Плотность сплавов

Представлена таблица значений плотности сплавов при комнатной температуре. Приведены следующие сплавы: бронза, оловянистая, фосфористая, дюралюминий, инвар, константан, латунь, магналиум, манганин, монель — металл, платино — иридиевый сплав, сплав Вуда, сталь катаная, литая.

ПРИМЕЧАНИЕ: Будьте внимательны! Плотность сплавов в таблице указана в степени 10-3. Не забудьте умножить на 1000! Например, плотность катанной стали изменяется в пределах от 7850 до 8000 кг/м3.

1. Михеев М.А., Михеева И.М. Основы теплопередачи.
2. Физические величины. Справочник. А.П. Бабичев, Н.А. Бабушкина, А.М. Братковский и др.; Под ред. И.С. Григорьева, Е.З. Мейлихова. — М.: Энергоатомиздат, 1991. — 1232 с.
3. Таблицы физических величин. Справочник. Под ред. акад. И.К. Кикоина. М.: Атомиздат, 1976. — 1008 с.
4. Шелудяк Ю.Е., Кашпоров Л.Я. и др. Теплофизические свойства компонентов горючих систем. М. 1992. — 184 с.
5. Промышленные печи. Справочное руководство для расчетов и проектирования. 2–е издание, дополненное и переработанное, Казанцев Е.И. М.: «Металлургия», 1975.- 368 с.

Электрическая проводимость

До сих пор мы рассматривали сопротивление проводника как препятствие, которое оказывает проводник электрическому току. Но все же ток по проводнику проходит. Следовательно, кроме сопротивления (препятствия), проводник обладает также способностью проводить электрический ток, то есть проводимостью.

Чем большим сопротивлением обладает проводник, тем меньшую он имеет проводимость, тем хуже он проводит электрический ток, и, наоборот, чем меньше сопротивление проводника, тем большей проводимостью он обладает, тем легче току пройти по проводнику. Поэтому сопротивление и проводимость проводника есть величины обратные.

Из математики известно, что число, обратное 5, есть 1/5 и, наоборот, число, обратное 1/7, есть 7. Следовательно, если сопротивление проводника обозначается буквой r, то проводимость определяется как 1/r. Обычно проводимость обозначается буквой g.

Электрическая проводимость измеряется в (1/Ом) или в сименсах.

Пример 8. Сопротивление проводника равно 20 Ом. Определить его проводимость.

Если r = 20 Ом, то

Пример 9. Проводимость проводника равна 0,1 (1/Ом). Определить его сопротивление,

Если g = 0,1 (1/Ом), то r = 1 / 0,1 = 10 (Ом)

Свойства полимеров: теплопроводность и плотность пластиков и пластмасс

В таблице представлены физические свойства полимеров (пластмасс и пластика) при отрицательной и положительной температуре, в интервале от -200 до 280°С. Свойства пластиков даны при нормальном атмосферном давлении.

Таблица свойств следующих полимеров, пластиков и пластмасс: акриловая смола, асбоволокниты типа КФ-3, асботекстолиты, асборезит, волокниты, гетинаксы, гетинакс тонкий, древеснослоистые пластики ДСП, карболит: крезольный, литой, фенольный, каучук, силиконовый, с наполнителем, кремнийорганический полимер КМ-9, кремнийорганическая смола К-55, К-18-2, К-21-22. Лак: алкидный на высыхающих маслах ФВ-2, пентафталевый №170, кремнийорганический КО-08, полиэфирный ПЭ-939, лак битумный №177, мипора, пенопласты, поропласты, полиамидная смола 54, полиамид 66 (полиамид 6, капрон, полиамид 66, нейлон, найлон), полиамид 68, поликапроамид, полиизобутен, поливинилбутираль, поливиниловый спирт, полиизобутилен, полиизопропилметакрилат, поликарбонат, полипропилен атактический, изоатактический, полиметилметакрилат, полиорганосилоксановые жидкости: ПМС — 1,5, ПМС — 5, 10, 50, 100, 200, 400, 476, 700, 1000, ПЭС — 1, 2, 3, 4, 5, ПФМС — 2/5 Л, 4, ФМ — 1322, ПФМС — 6, полистирол ударопрочный УПП — 1 ППС, политетрафторэтилен, полихлортрифторэтилен, полиуретан ПУ — 1, ПВХ пленка, кабельный, пластифицированный, жесткий, с кварцевым наполнителем, линолеум с наполнителем, хлорированный, полихлорвинил с бутилбензилфталатом, палатиновое масло АН, полиэтилен ВД, П2020, ПЭ — 500, линейный, НД, П4045К, полиэтилентерефталат, полиэтиленгликоль, полиэтиленсилоксановая жидкость №5, 7, резит, резина пористая, стеклопластик полиэфирный на основе жесткого и мягкого стеклохолста, стекловолокнит типа АГ — 4, КАСТ, стеклопластик полиэфирный на основе стеклоткани, наполненной минеральным наполнителем 8% ZnO в смоле ПН-1, текстолит, фибролит, фенолформальдегидная смола, аррезин — Б, 101К, Р-21, совмещенный фенолит, фенольная литая смола, фурфурил — фенолформальдегидная смола Ф-10, фурановый полимер ФГ-2, эмаль (кремнийорганическая): КО-84, КО-811, эпоксидная смола Э-33, Э-41, ЭД-5, ТФЭ-9, ПН-1, этрол ацетатцеллюлозный, этилцеллюлозный.

Даны следующие теплофизические свойства полимеров и пластмасс:

• плотность пластика, кг/м3;
• коэффициент теплопроводности, Вт/(м·град);
• коэффициент температуропроводности, м2/с;
• удельная (массовая) теплоемкость, кДж/(кг·град).

Следует особо отметить значения плотности пластмассы в таблице. Ее диапазон находится в пределах от 16 кг/м3  (для теплоизоляционных пенистых пластмасс — таких, как мипора) до 2280 кг/м3 (для тяжелого линолеума с наполнителем).

Удельное сопротивление кабеля таблица

Главная > Теория > Удельное сопротивление меди

Формула вычисления сопротивления проводника

Что такое электрический ток

На разных полюсах аккумулятора или другого источника тока есть разноимённые носители электрического заряда. Если их соединить с проводником, носители заряда начинают движение от одного полюса источника напряжения к другому. Этими носителями в жидкости являются ионы, а в металлах – свободные электроны.

Определение. Электрический ток – это направленное движение заряженных частиц.

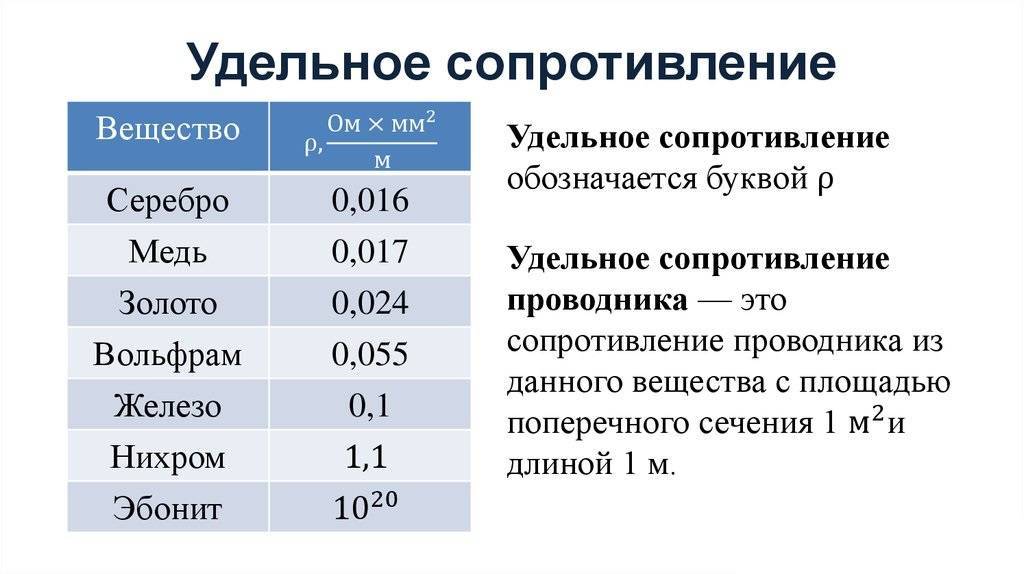
Удельное сопротивление

Удельное электрическое сопротивление – это величина, определяющая электросопротивление эталонного образца материала. Для обозначения этой величины используется греческая буква «р». Формула для расчета:

p=(R*S)/l.

Эта величина измеряется в Ом*м. Найти её можно в справочниках, в таблицах удельного сопротивления или в сети интернет.

Свободные электроны по металлу двигаются внутри кристаллической решётки. На сопротивление этому движению и удельное сопротивление проводника влияют три фактора:

• Материал. У разных металлов различная плотность атомов и количество свободных электронов;
• Примеси. В чистых металлах кристаллическая решётка более упорядоченная, поэтому сопротивление ниже, чем в сплавах;
• Температура. Атомы не находятся на своих местах неподвижно, а колеблются. Чем выше температура, тем больше амплитуда колебаний, создающая помехи движению электронов, и выше сопротивление.

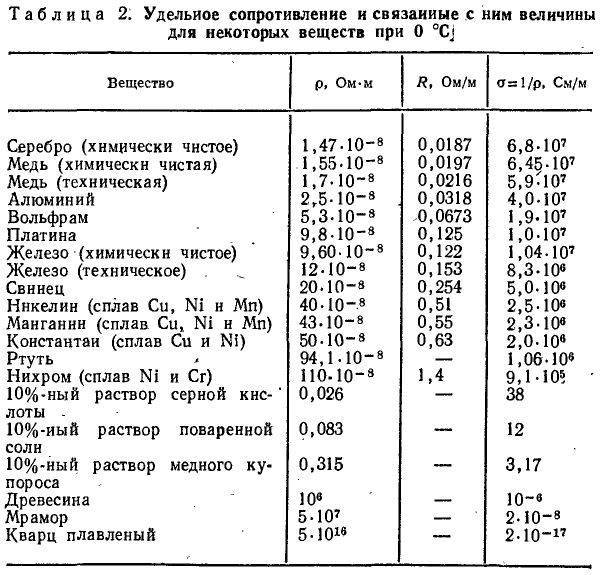
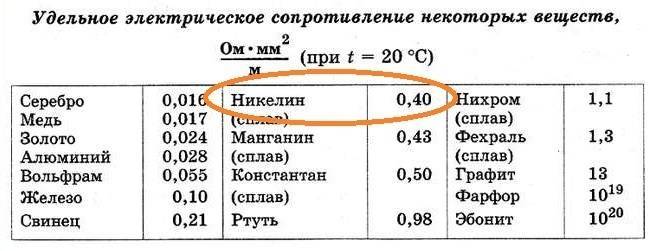
На следующем рисунке можно увидеть таблицу удельного сопротивления металлов.

Удельное сопротивление металлов

Интересно. Есть сплавы, электросопротивление которых падает при нагреве или не меняется.

Проводимость и электросопротивление

Так как размеры кабелей измеряются в метрах (длина) и мм² (сечение), то удельное электрическое сопротивление имеет размерность Ом·мм²/м. Зная размеры кабеля, его сопротивление рассчитывается по формуле:

R=(p*l)/S.

Кроме электросопротивления, в некоторых формулах используется понятие «проводимость». Это величина, обратная сопротивлению. Обозначается она «g» и рассчитывается по формуле:

g=1/R.

Проводимость жидкостей

Проводимость жидкостей отличается от проводимости металлов. Носителями зарядов в них являются ионы. Их количество и электропроводность растут при нагревании, поэтому мощность электродного котла растёт при нагреве от 20 до 100 градусов в несколько раз.

Интересно. Дистиллированная вода является изолятором. Проводимость ей придают растворенные примеси.

Электросопротивление проводов

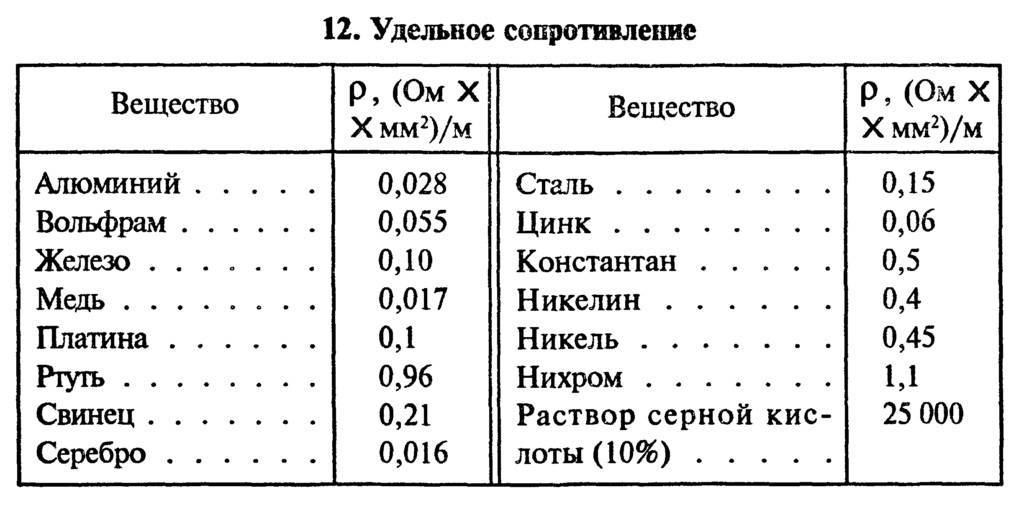
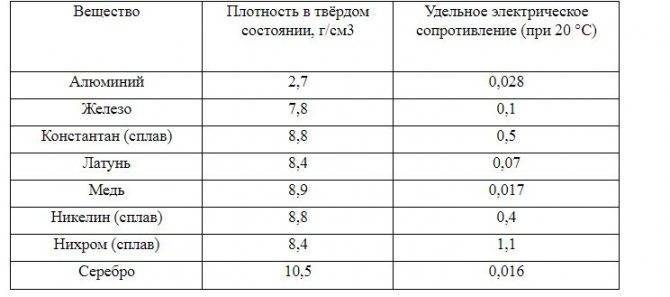
Самые распространенные металлы для изготовления проводов – медь и алюминий. Сопротивление алюминия выше, но он дешевле меди. Удельное сопротивление меди ниже, поэтому сечение проводов можно выбрать меньше. Кроме того, она прочнее, и из этого металла изготавливаются гибкие многожильные провода.

В следующей таблице показывается удельное электросопротивление металлов при 20 градусах. Для того чтобы определить его при других температурах, значение из таблицы необходимо умножить на поправочный коэффициент, различный для каждого металла. Узнать этот коэффициент можно из соответствующих справочников или при помощи онлайн-калькулятора.

Сопротивление проводов

Выбор сечения кабеля

Поскольку у провода есть сопротивление, при прохождении по нему электрического тока выделяется тепло, и происходит падение напряжения. Оба этих фактора необходимо учитывать при выборе сечения кабелей.

Выбор по допустимому нагреву

При протекании тока в проводе выделяется энергия. Её количество можно рассчитать по формуле электрической мощности:

P=I²*R.

В медном проводе сечением 2,5мм² и длиной 10 метров R=10*0.0074=0.074Ом. При токе 30А Р=30²*0,074=66Вт.

Эта мощность нагревает токопроводящую жилу и сам кабель. Температура, до которой он нагревается, зависит от условий прокладки, числа жил в кабеле и других факторов, а допустимая температура – от материала изоляции. Медь обладает большей проводимостью, поэтому меньше выделяемая мощность и необходимое сечение. Определяется оно по специальным таблицам или при помощи онлайн-калькулятора.

Таблица выбора сечения провода по допустимому нагреву

2.1.1. Физическая природа электропроводности металлов

Металлы имеют кристаллическое строение: в узлах кристаллической решетки находятся положительно заряженные ионы, окруженные коллективизированными электронами (электронным газом).

Современные представления об электронном строении металлов, распределении электронов по энергетическим состояниям, их взаимодействии с другими элементарными частицами и кристаллической решеткой дает квантовая теория, основы которой были разработаны советским ученым Я.И.Френкелем и немецким физиком А.Зоммерфельдом.

Читать также: Самый лучший бюджетный шуруповерт

Свободные электроны хаотически перемещаются по кристаллу со средней тепловой скоростью и = 10 5 м/с. В электрическом поле напряженностью Е электроны получают добавочную скорость упорядоченного движения v — скорость дрейфа, благодаря чему и возникает электрический ток. Плотность тока зависит от скорости дрейфа, заряда электрона е и концентрации свободных электронов n .

Скорость дрейфа в реальных условиях существенно меньше скорости теплового движения электронов v u . Так, в медном про-

воднике при плотности тока j = 1 А/мм 2 скорость дрейфа составляет v = 1 . 10 -4 м/с.

За время τ между столкновениями с узлами кристаллической решетки на длине свободного пробега l , электроны, двигаясь с уско-

рением a = e E , приобретают скорость дрейфа: m e

Приравнивая аналитическое выражение закона Ома (1.1) к выражению (2.1) с учетом (2.2), получим формулу для удельной проводимости

Выразим произведение m e . и через концентрацию свободных электронов, используя квантовую статистику, базирующуюся на принципе Паули, согласно которому в каждом энергетическом состоянии может находиться только один электрон, а на каждом энергетическом уровне — не более двух (с антипараллельными спинами). Тогда при температуре абсолютного нуля ( Т = 0 К) половина из общего числа свободных электронов в кристалле ( n /2) займет наиболее низкие энергетические уровни.

В квантовой теории вероятность заполнения электронами энергетических состояний с энергией уровня Э определяется функцией Ферми

где Э F — энергия Ферми, т.е. максимальная энергия, которую может иметь электрон в металле при температуре абсолютного нуля.

Из формулы (2.4) следует, что при Э = Э F , вероятность заполнения электронами уровня Ферми равна 0,5. Энергия Ферми для большинства металлов составляет от 3 до 15 эВ. Уровни, расположенные ниже уровня Ферми ( Э Э F ), с вероятностью >0,5 заполнены электронами, а уровни, лежащие выше уровня Ферми ( Э > Э F ), с такой же вероятностью свободны от электронов.

В соответствии с квантовой статистикой Ферми-Дирака концентрация свободных электронов в металле определяется путем интег-

рирования по всем заполненным энергетическим состояниям, что дает следующее выражение

Выразив из этого соотношения значение энергии Ферми через концентрацию электронов и, учитывая, что Э F = m e и 2 2 , получим

Подставляя m e и в формулу (2.3), найдем выражение для

удельной проводимости металлов

Концентрация свободных электронов в чистых металлах, характер их распределения по энергиям и энергия Ферми с повышением температуры почти не изменяются. Например, при нагреве серебра от 0 до 1000 К энергия Ферми уменьшается лишь на 0,2%. Такие малые изменения в широком температурном диапазоне можно не учитывать. Следовательно, формула (2.6) справедлива при любой температуре. Поэтому электропроводность металла определяется, в основном, средней длиной свободного пробега электронов, которая зависит от электронного строения атомов и типа кристаллической решетки. Длина свободного пробега для некоторых металлов дана в табл. 1.

Длина свободного пробега электронов в некоторых металлах при 0 ° С

Наибольшая длина свободного пробега наблюдается в металлах с гранецентрированной кубической кристаллической решеткой (Ag, Cu, Au), которые и являются лучшими проводниками.

Переходные металлы (Fe, Ni, Co, Cr, Mn, V, Zr, Nb, Mo, W, Hf, Ta, Re, Pt и др.) имеют меньшую электропроводность, что связано с их специфическим электронным строением. В этих элементах внутренние d — или f -оболочки неполностью заполнены электронами. В электрическом поле часть валентных электронов из внешней s — оболочки переходят на свободные уровни внутренних оболочек, что приводит к уменьшению числа свободных электронов, участвующих в проводимости.

Особенности электронного строения переходных металлов являются причиной многих их специфических свойств: тепловых, магнитных, склонности к полиморфизму, переменной валентности и др.

И в заключение, у чистых металлов при нагреве средняя энергия электронов практически остается без изменения, что свидетельствует о малой теплоемкости электронного газа.

Электрическая проводимость

До сих пор мы рассматривали сопротивление проводника как препятствие, которое оказывает проводник электрическому току. Но все же ток по проводнику проходит. Следовательно, кроме сопротивления (препятствия), проводник обладает также способностью проводить электрический ток, то есть проводимостью.

Чем большим сопротивлением обладает проводник, тем меньшую он имеет проводимость, тем хуже он проводит электрический ток, и, наоборот, чем меньше сопротивление проводника, тем большей проводимостью он обладает, тем легче току пройти по проводнику. Поэтому сопротивление и проводимость проводника есть величины обратные.

Из математики известно, что число, обратное 5, есть 1/5 и, наоборот, число, обратное 1/7, есть 7. Следовательно, если сопротивление проводника обозначается буквой r, то проводимость определяется как 1/r. Обычно проводимость обозначается буквой g.

Электрическая проводимость измеряется в (1/Ом) или в сименсах.

Пример 8. Сопротивление проводника равно 20 Ом. Определить его проводимость.

Если r = 20 Ом, то

Пример 9. Проводимость проводника равна 0,1 (1/Ом). Определить его сопротивление,

Если g = 0,1 (1/Ом), то r = 1 / 0,1 = 10 (Ом)

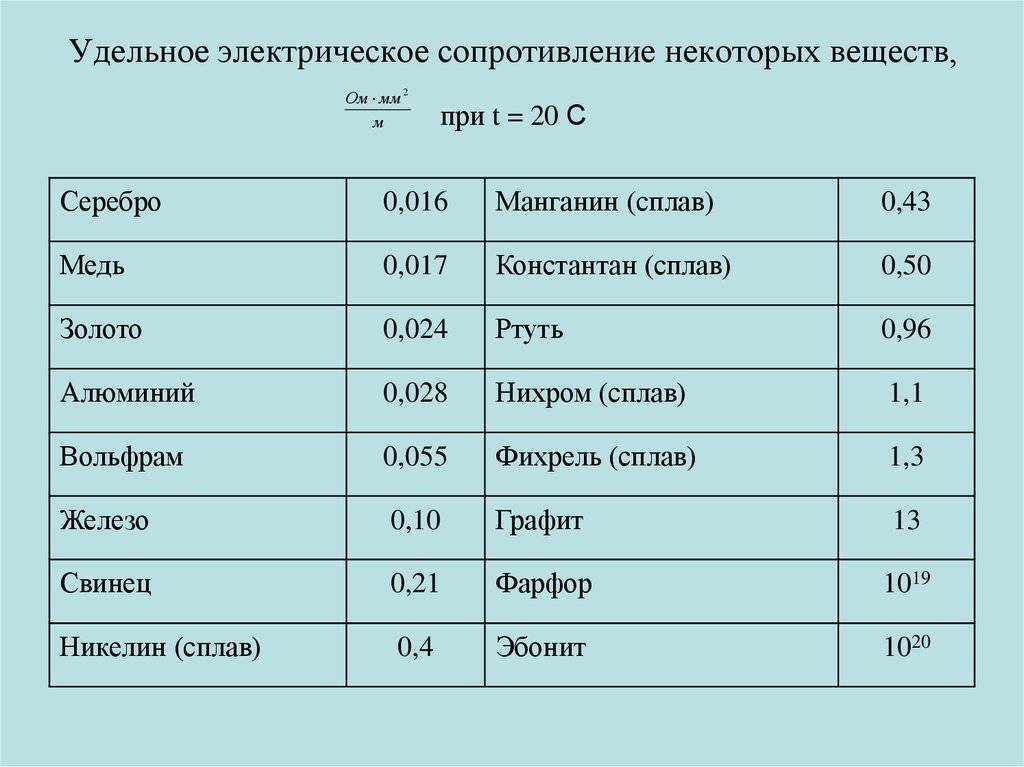
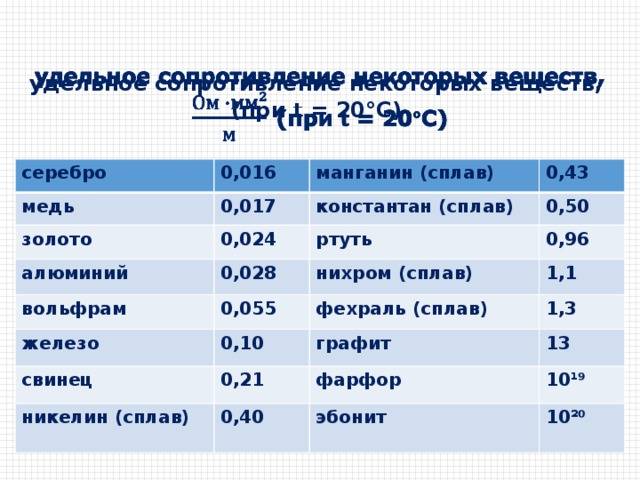
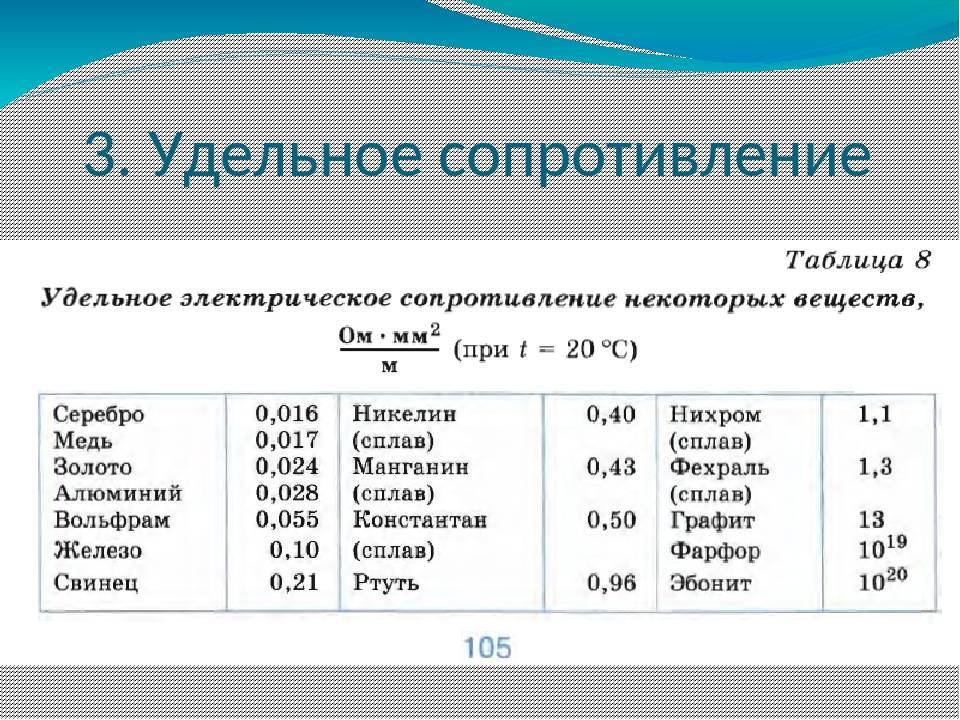
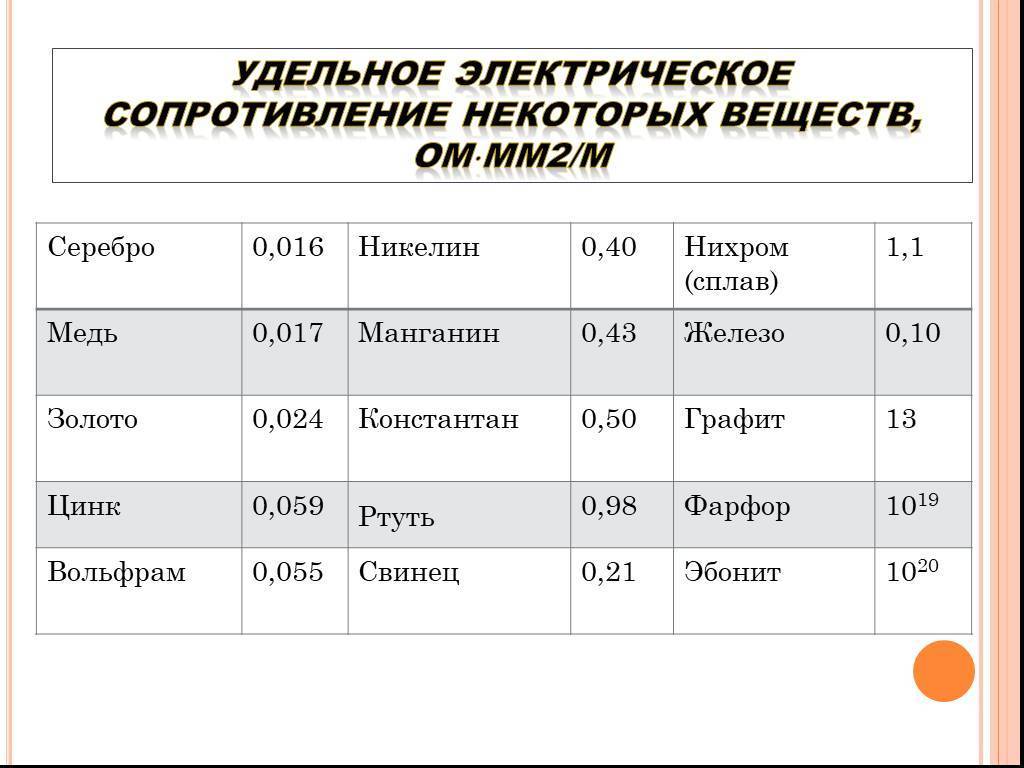
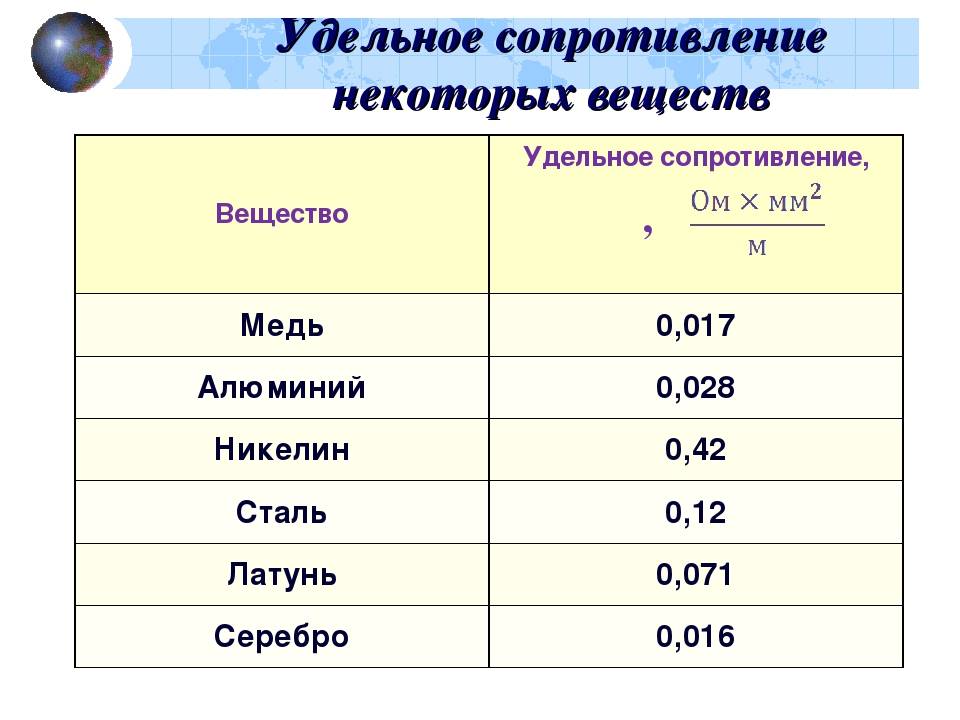
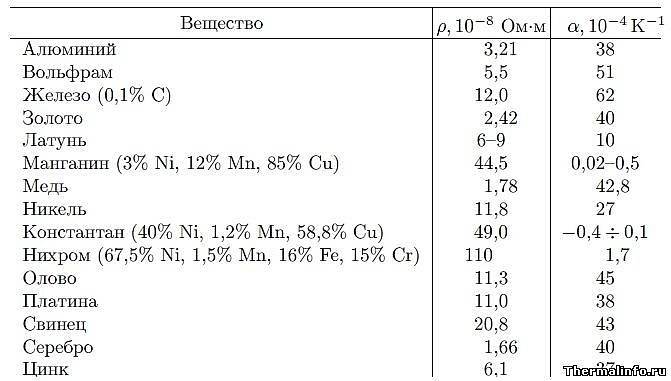
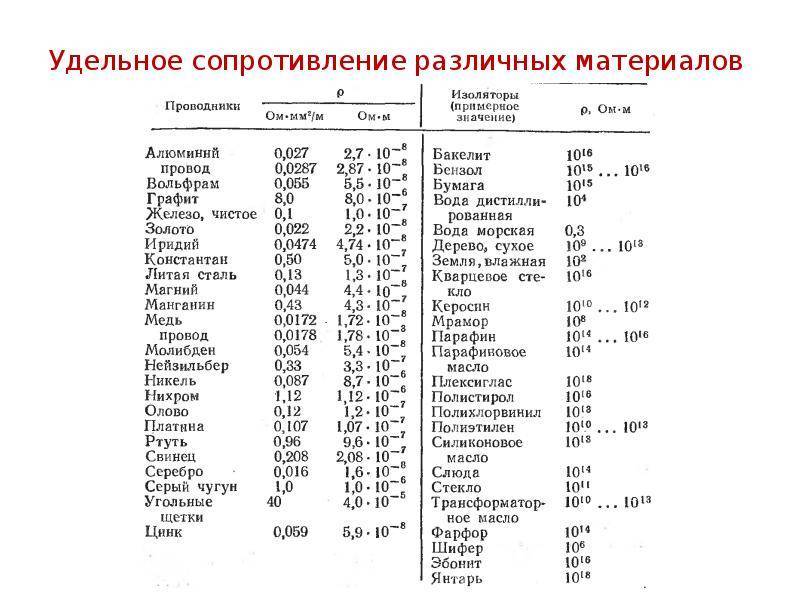
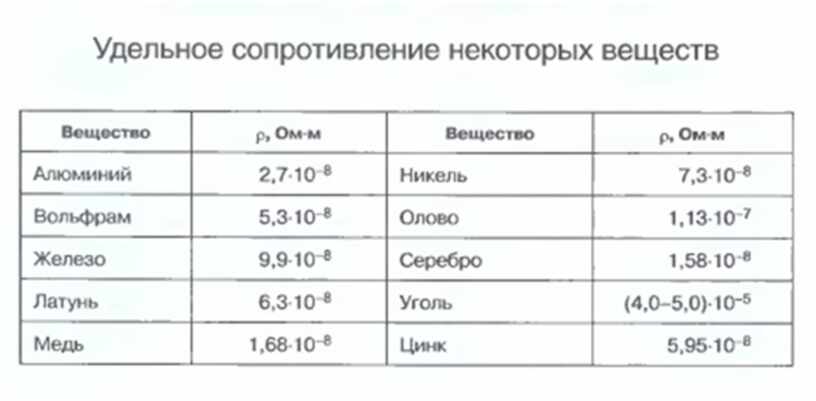
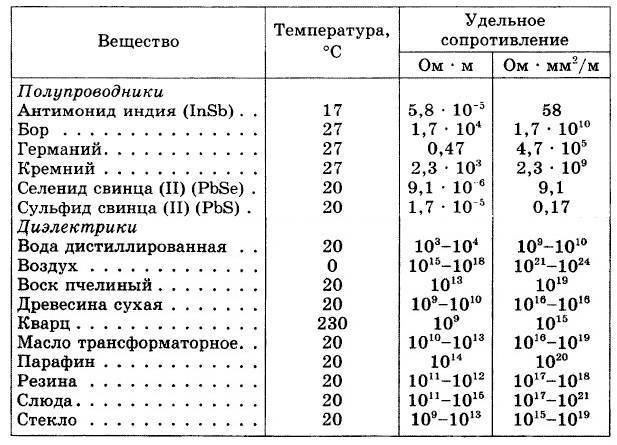
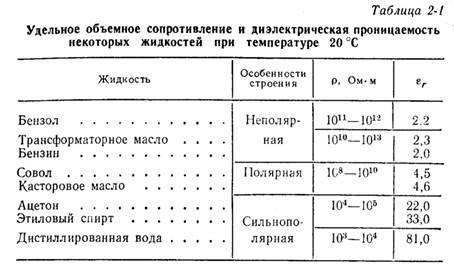
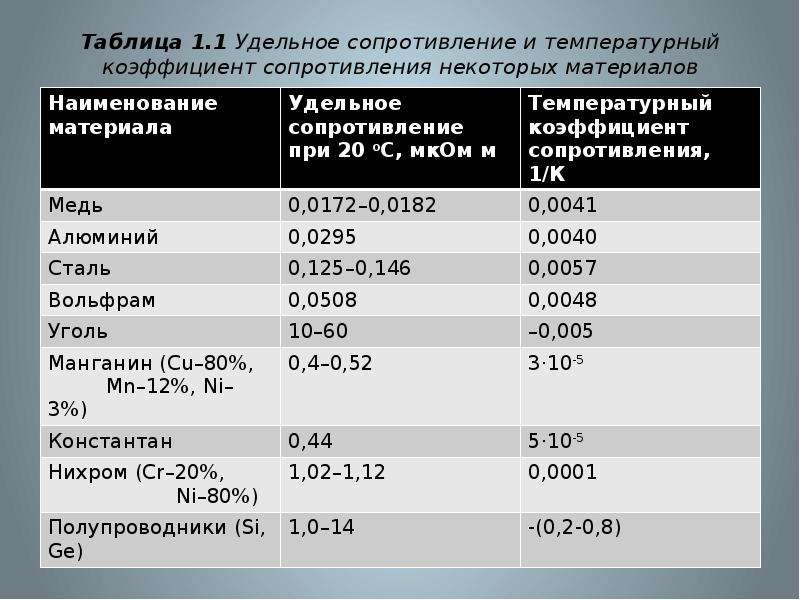
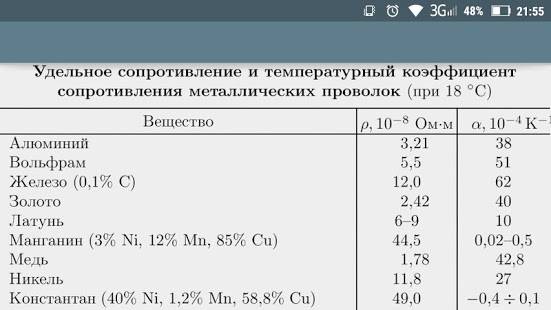
Удельное электрическое сопротивление некоторых веществ[ | ]

Металлические монокристаллы

В таблице приведены главные значения тензора удельного сопротивления монокристаллов при температуре 20 °C.

Кристалл	ρ1=ρ2, 10−8 Ом·м	ρ3, 10−8 Ом·м
Олово	9,9	14,3
Висмут	109	138
Кадмий	6,8	8,3
Цинк	5,91	6,13
Теллур	2,90·109	5,9·109

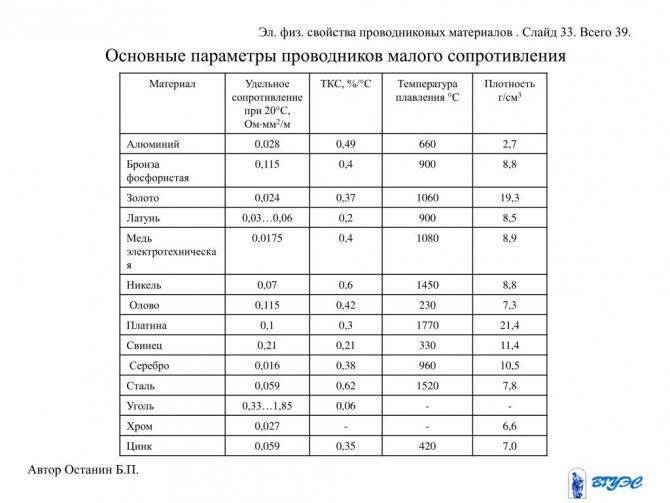
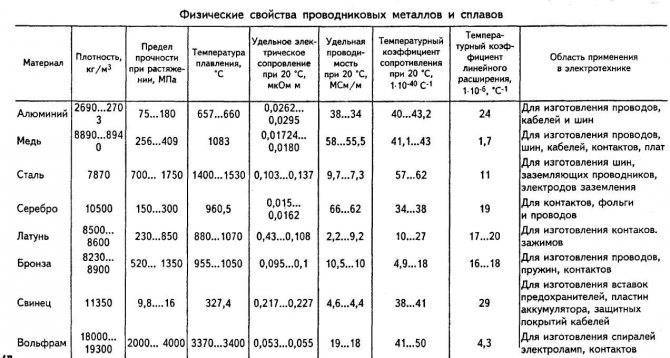
Металлы и сплавы, применяемые в электротехнике

В этом разделе не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 10 ноября 2021 года

Разброс значений обусловлен разной химической чистотой металлов, способами изготовления образцов, изученных разными учеными, и непостоянством состава сплавов.

	0,015…0,0162
Медь	0,01707…0,018
Медь 6N Cu 99.9999%	0,01673
Золото	0,023
Алюминий	0,0262…0,0295
Иридий	0,0474
Натрий	0,0485
Молибден	0,054
Вольфрам	0,053…0,055
Цинк	0,059
Индий	0,0837
Никель	0,087
Железо	0,099
Платина	0,107
Олово	0,12
Свинец	0,217…0,227
Титан	0,5562…0,7837
Ртуть	0,958
Висмут	1,2

Никелин	0,42
Константан	0,5
Манганин	0,43…0,51
Нихром	1,05…1,4
Фехраль	1,15…1,35
Хромаль	1,3…1,5
Латунь	0,025…0,108
Бронза	0,095…0,1

Значения даны при температуре t

= 20 °C. Сопротивления сплавов зависят от их химического состава и могут варьироваться. Для чистых веществ колебания численных значений удельного сопротивления обусловлены различными методами механической и термической обработки, например, отжигом проволоки после волочения.

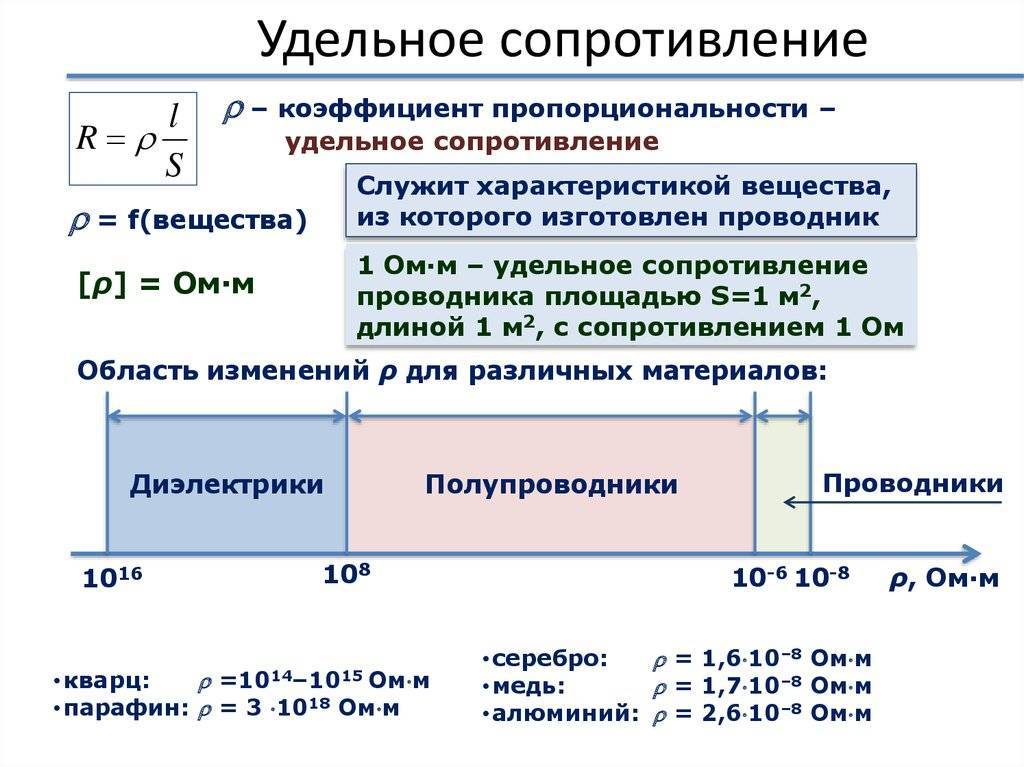
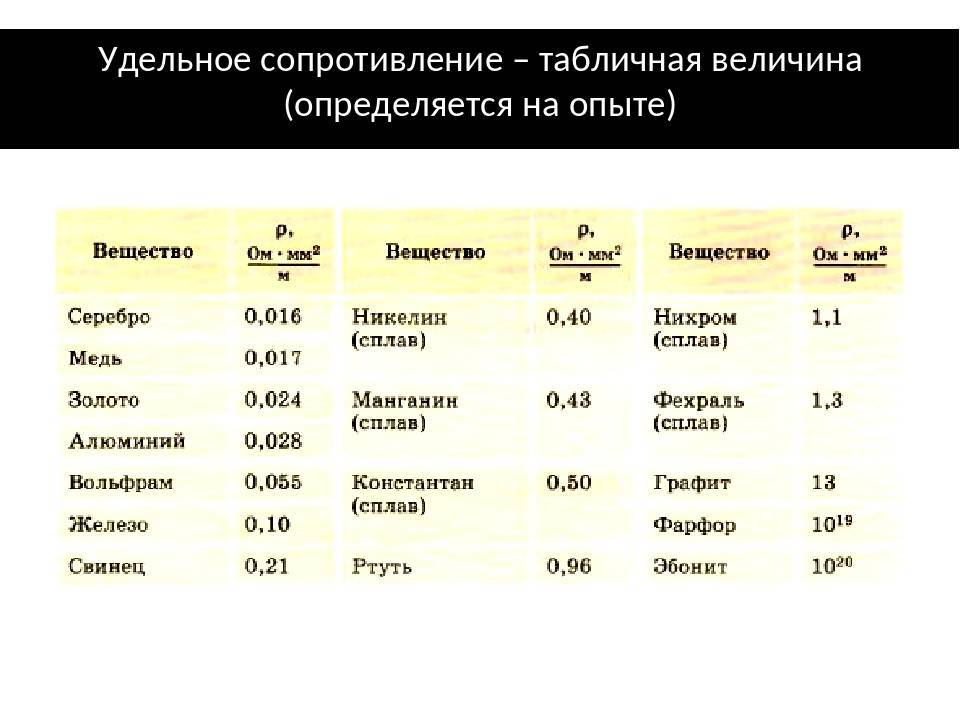
§ 45. Расчёт сопротивления проводника. Удельное сопротивление

Мы знаем, что причиной электрического сопротивления проводника является взаимодействие электронов с ионами кристаллической решётки металла (§ 43). Поэтому можно предположить, что сопротивление проводника зависит от его длины и площади поперечного сечения, а также от вещества, из которого он изготовлен.

На рисунке 74 изображена установка для проведения такого опыта. В цепь источника тока по очереди включают различные проводники, например:

1. никелиновые проволоки одинаковой толщины, но разной длины;
2. никелиновые проволоки одинаковой длины, но разной толщины (разной площади поперечного сечения);
3. никелиновую и нихромовую проволоки одинаковой длины и толщины.

Силу тока в цепи измеряют амперметром, напряжение — вольтметром.

Зная напряжение на концах проводника и силу тока в нём, по закону Ома можно определить сопротивление каждого из проводников.

Рис. 74. Зависимость сопротивления проводника от его размеров и рода вещества

Выполнив указанные опыты, мы установим, что:

1. из двух никелиновых проволок одинаковой толщины более длинная проволока имеет большее сопротивление;
2. из двух никелиновых проволок одинаковой длины большее сопротивление имеет проволока, поперечное сечение которой меньше;
3. никелиновая и нихромовая проволоки одинаковых размеров имеют разное сопротивление.

Зависимость сопротивления проводника от его размеров и вещества, из которого изготовлен проводник, впервые на опытах изучил Ом. Он установил, что сопротивление прямо пропорционально длине проводника, обратно пропорционально площади его поперечного сечения и зависит от вещества проводника.

Как учесть зависимость сопротивления от вещества, из которого изготовляют проводник? Для этого вычисляют так называемое удельное сопротивление вещества.

Удельное сопротивление — это физическая величина, которая определяет сопротивление проводника из данного вещества длиной 1 м, площадью поперечного сечения 1 м2.

Введём буквенные обозначения: ρ — удельное сопротивление проводника, I — длина проводника, S — площадь его поперечного сечения. Тогда сопротивление проводника R выразится формулой

Из неё получим, что:

Из последней формулы можно определить единицу удельного сопротивления. Так как единицей сопротивления является 1 Ом, единицей площади поперечного сечения — 1 м2, а единицей длины — 1 м, то единицей удельного сопротивления будет:

Удобнее выражать площадь поперечного сечения проводника в квадратных миллиметpax, так как она чаще всего бывает небольшой. Тогда единицей удельного сопротивления будет:

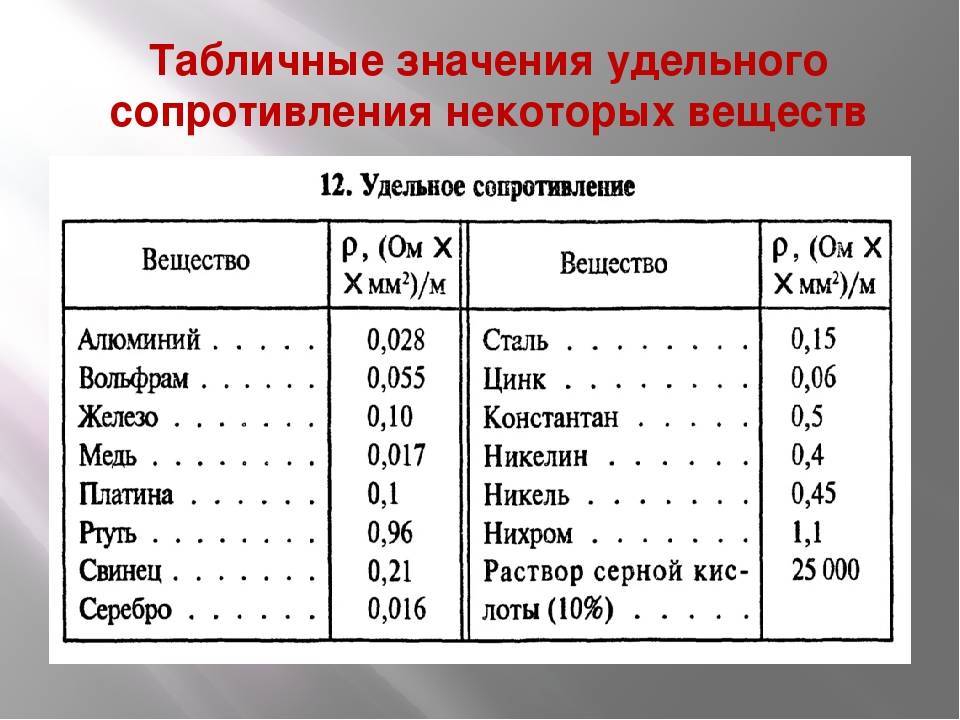
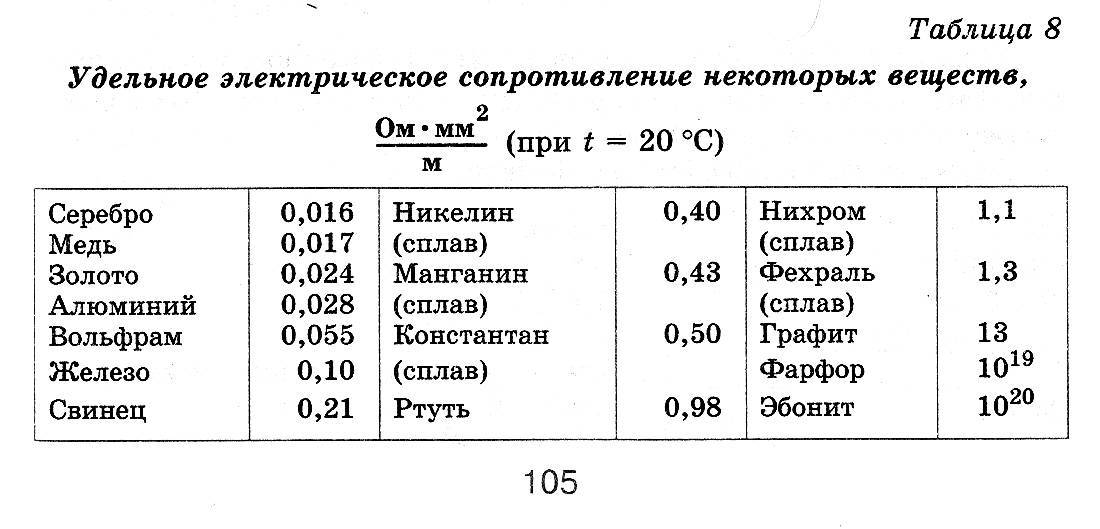
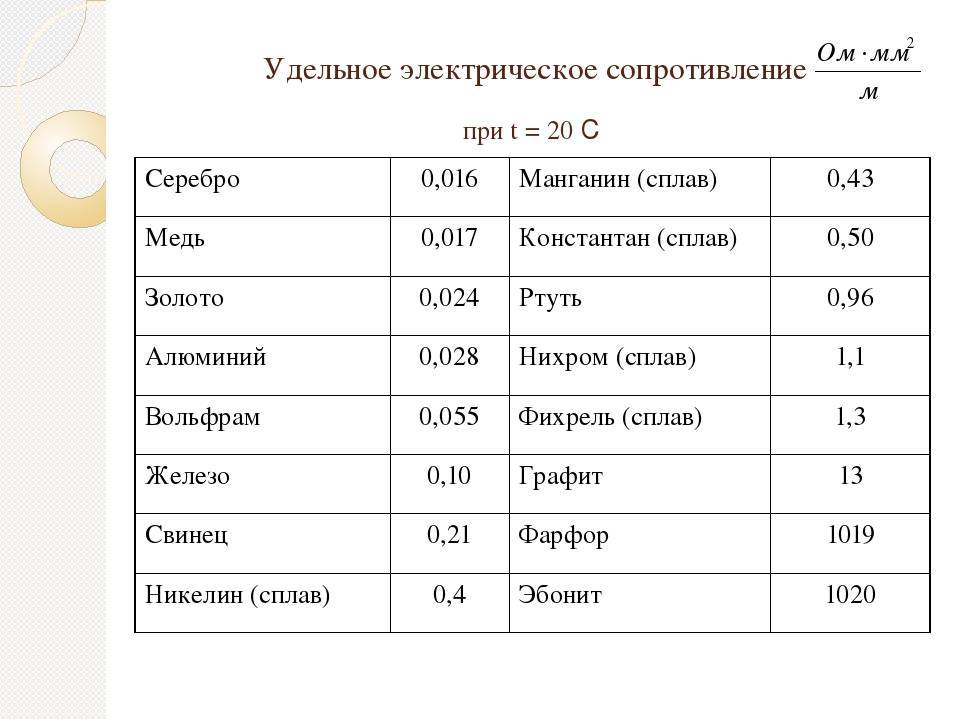
В таблице 8 приведены значения удельных сопротивлений некоторых веществ при 20 °С. Удельное сопротивление с изменением температуры меняется. Опытным путём было установлено, что у металлов, например, удельное сопротивление с повышением температуры увеличивается.

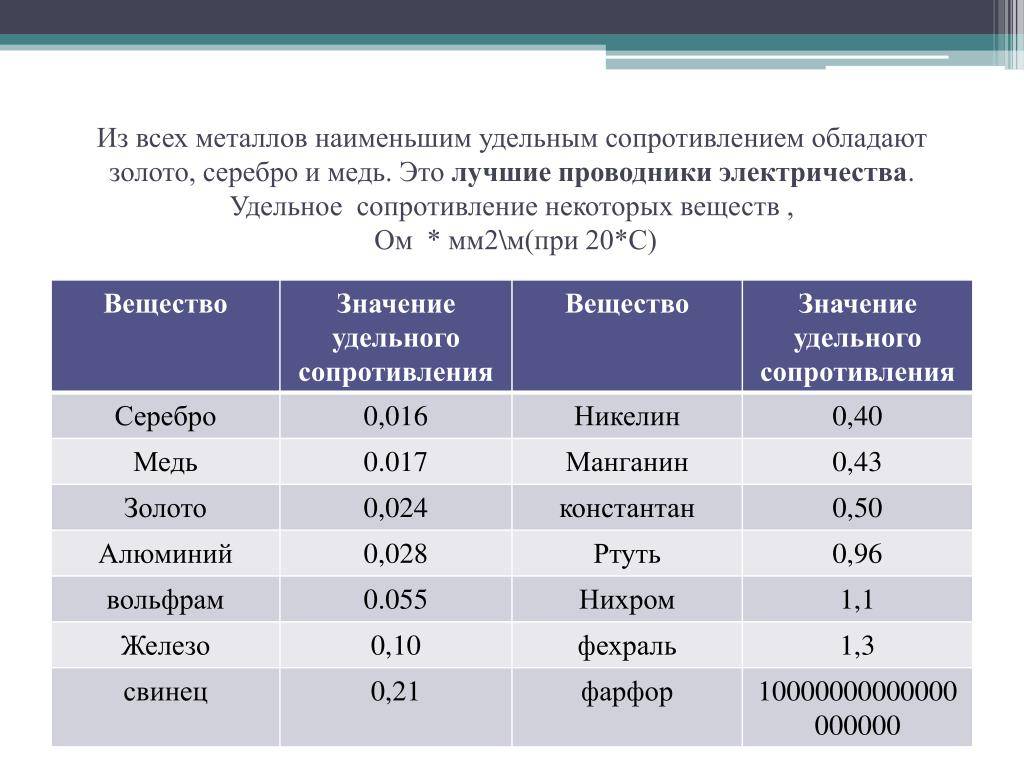
Таблица 8. Удельное электрическое сопротивление некоторых веществ (при t = 20 °С)

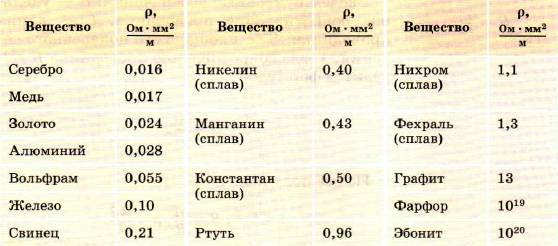
Из всех металлов наименьшим удельным сопротивлением обладают серебро и медь. Следовательно, серебро и медь — лучшие проводники электричества.

При проводке электрических цепей используют алюминиевые, медные и железные провода.

Во многих случаях бывают нужны приборы, имеющие большое сопротивление. Их изготавливают из специально созданных сплавов — веществ с большим удельным сопротивлением. Например, как видно из таблицы 8, сплав нихром имеет удельное сопротивление почти в 40 раз большее, чем алюминий.

Фарфор и эбонит имеют такое большое удельное сопротивление, что почти совсем не проводят электрический ток, их используют в качестве изоляторов.

Вопросы

1. Как зависит сопротивление проводника от его длины и от площади поперечного сечения?
2. Как показать на опыте зависимость сопротивления проводника от его длины, площади поперечного сечения и вещества, из которого он изготовлен?
3. Что называется удельным сопротивлением проводника?
4. По какой формуле можно рассчитывать сопротивление проводников?
5. В каких единицах выражается удельное сопротивление проводника?
6. Из каких веществ изготавливают проводники, применяемые на практике?

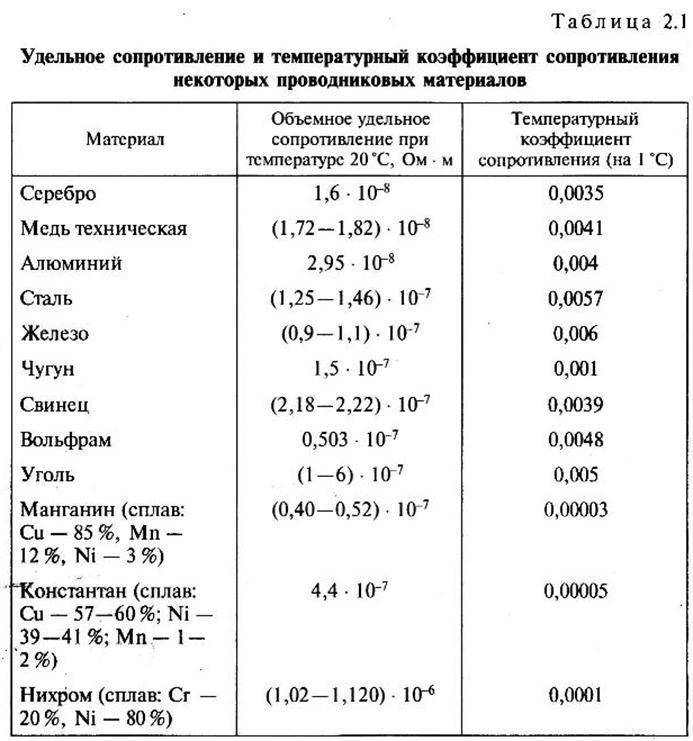
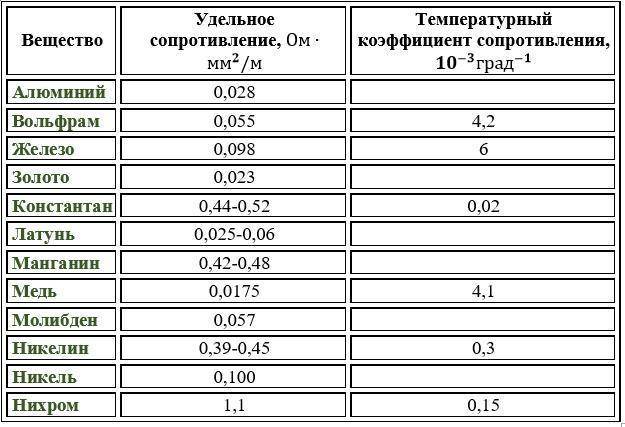
Значения температурного коэффициента для некоторых металлов

Металл	α		Металл	α
Серебро Медь Железо Вольфрам Платина	0,0035 0,0040 0,0066 0,0045 0,0032	Ртуть Никелин Константан Нихром Манганин	0,0090 0,0003 0,000005 0,00016 0,00005

Из формулы температурного коэффициента сопротивления определим r_t:

r_t = r .

Пример 6. Определить сопротивление железной проволоки, нагретой до 200°C, если сопротивление ее при 0°C было 100 Ом.

r_t = r = 100 (1 + 0,0066 α 200) = 232 Ом.

Пример 7. Термометр сопротивления, изготовленный из платиновой проволоки, в помещении с температурой 15°C имел сопротивление 20 Ом. Термометр поместили в печь и через некоторое время было измерено его сопротивление. Оно оказалось равным 29,6 Ом. Определить температуру в печи.

Значения температурного коэффициента для некоторых металлов

Металл	α		Металл	α
Серебро Медь Железо Вольфрам Платина	0,0035 0,0040 0,0066 0,0045 0,0032	Ртуть Никелин Константан Нихром Манганин	0,0090 0,0003 0,000005 0,00016 0,00005

Из формулы температурного коэффициента сопротивления определим rt:

rt = r0 .

Пример 6. Определить сопротивление железной проволоки, нагретой до 200°C, если сопротивление ее при 0°C было 100 Ом.

rt = r0 = 100 (1 + 0,0066 α 200) = 232 Ом.

Пример 7. Термометр сопротивления, изготовленный из платиновой проволоки, в помещении с температурой 15°C имел сопротивление 20 Ом. Термометр поместили в печь и через некоторое время было измерено его сопротивление. Оно оказалось равным 29,6 Ом. Определить температуру в печи.

2.1.2. Температурная зависимость удельного сопротивления металлов

Рассмотрим движение свободных электронов в виде плоских электронных волн, длина которых λ определяется соотношением де Бройля (1.3). Такая электронная волна распространяется в строго периодическом потенциальном поле без рассеяния энергии. Это означает, что в идеальном кристалле длина свободного пробега электронов равна бесконечности, а сопротивление электрическому току равно нулю.

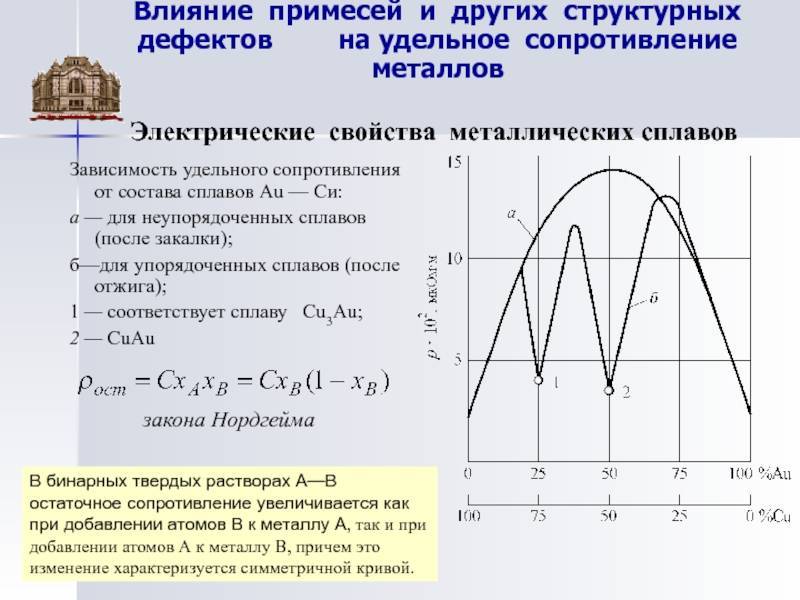
Причинами рассеяния электронов в реальных металлах, создающего электрическое сопротивление, являются:

• тепловые колебания узлов кристаллической решетки ( ρ т — тепловая составляющая электрического сопротивления);

• примеси и дефекты структуры ( ρ ост — составляющая ρ , обусловленная нетепловыми факторами).

Известно, что эффективное рассеяние энергии электронов происходит в том случае, если размер рассеивающих центров (дефектов) превышает 1/4 длины волны. В металлах энергия электронов

проводимости составляет 3…15 эВ, этой энергии соответствует длина электронной волны λ = 0,3…0,7нм. Поэтому любые микронеоднородности и несовершенства кристаллического строения вызывают снижение проводимости.

Читать также: Что можно сделать из профиля

Итак, удельное сопротивление реальных металлов представляет собой сумму двух составляющих:

Относительное изменение удельного сопротивления металлов при изменении температуры характеризует температурный ко-

Удельное сопротивление металлов является мерой их свойства противодействовать прохождению электрического тока. Эта величина выражается в Ом-метр (Ом⋅м).

Символ, обозначающий удельное сопротивление, является греческая буква ρ (ро). Высокое удельное сопротивление означает, что материал плохо проводит электрический заряд.