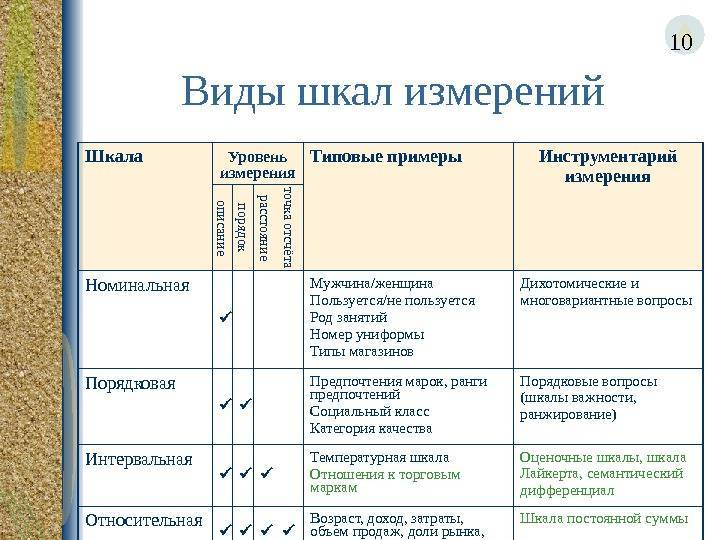
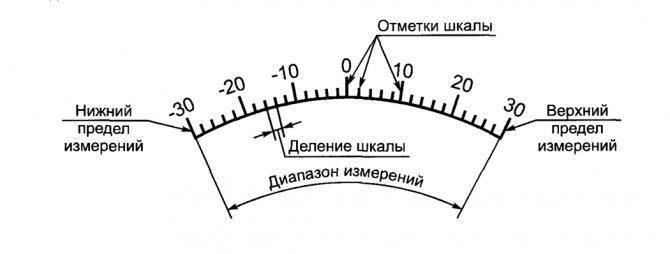
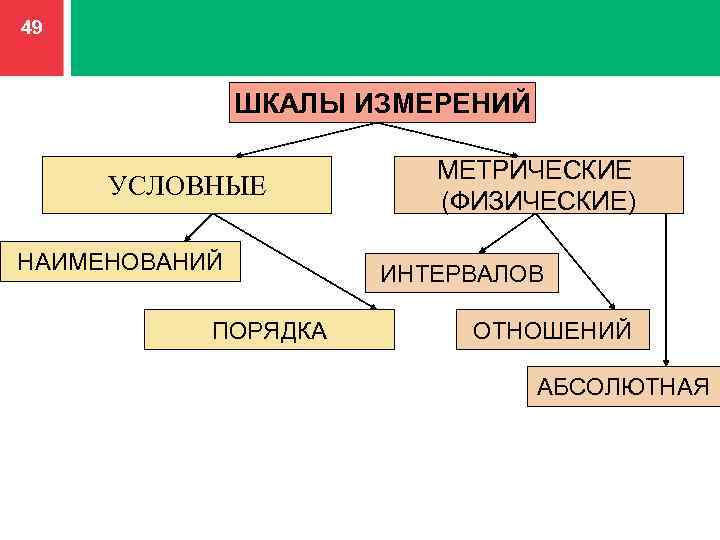
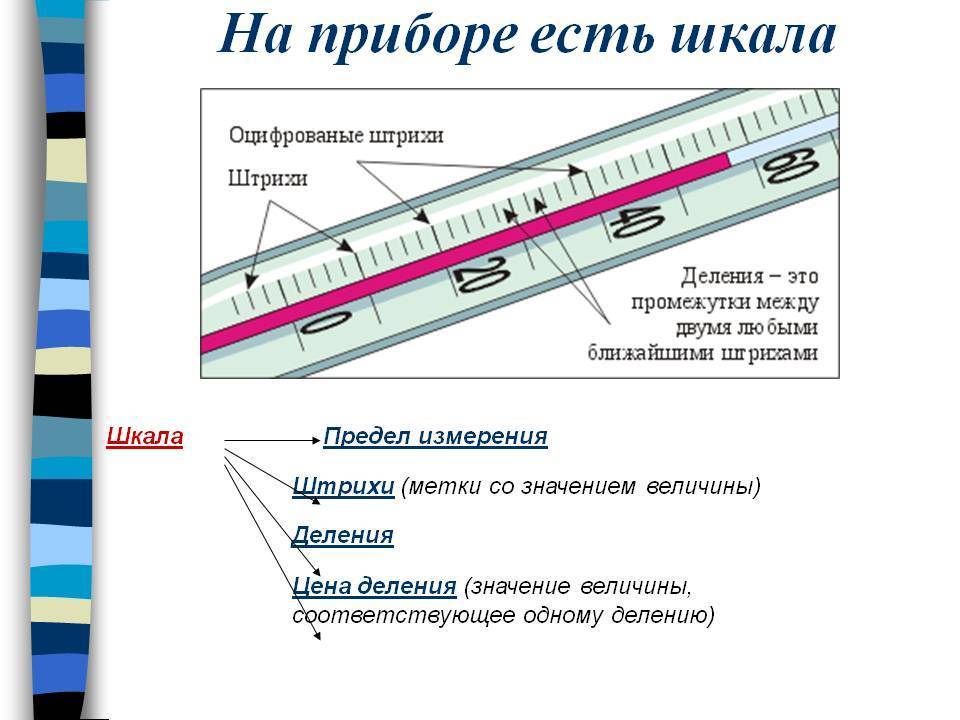
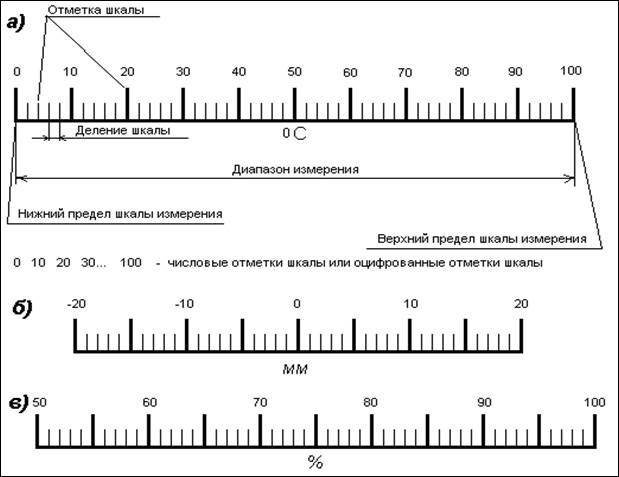
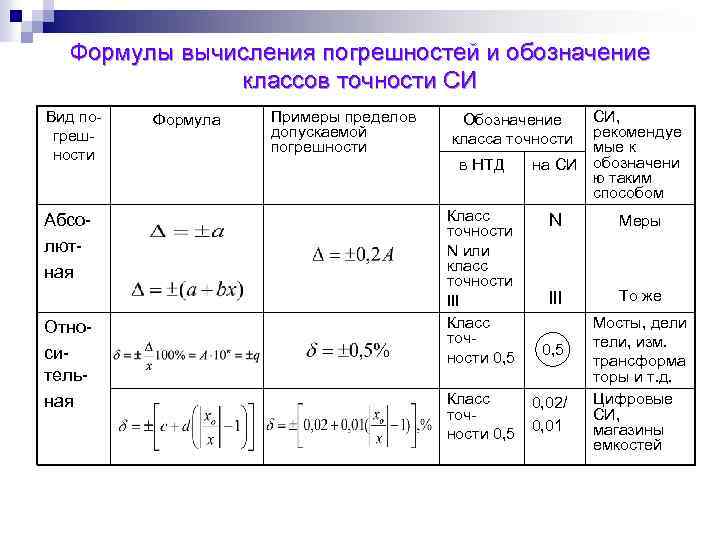
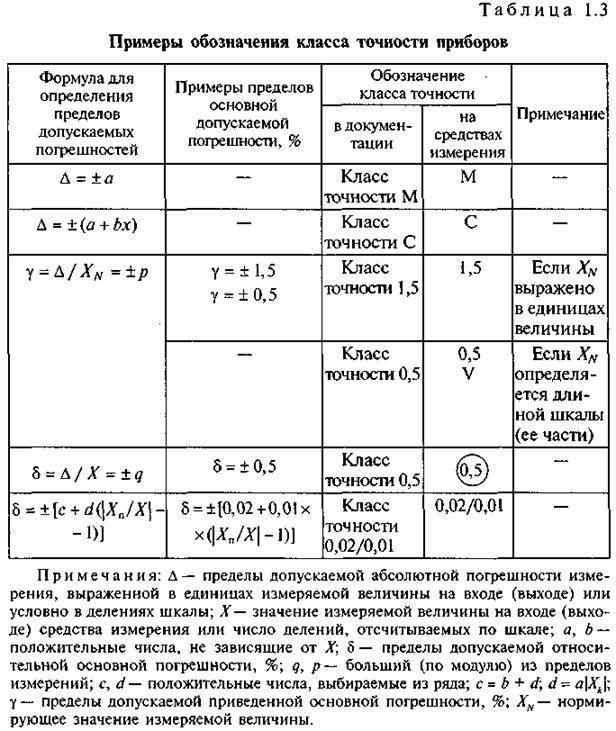
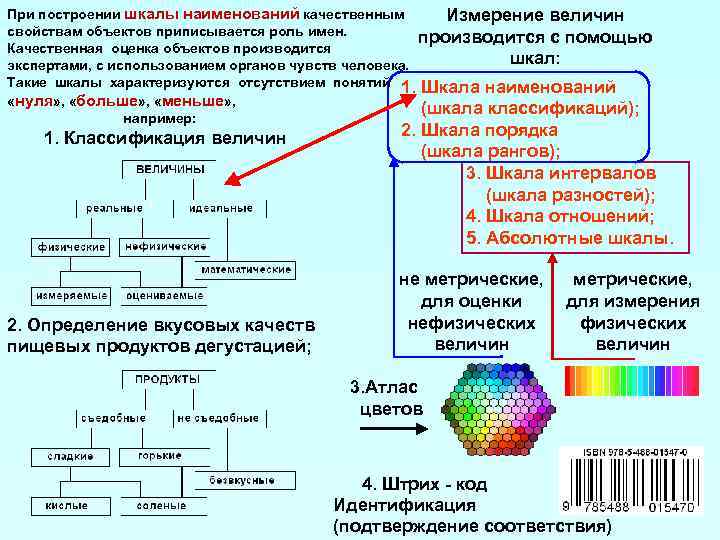
Шкала порядка
Места, которые величины занимают в такой шкале, называются рангами. Саму шкалу также называют ранговой либо неметрической. В ней все числа упорядочиваются по занимаемым местам. Интервалы между ними нельзя точно измерить. Данная шкала дает возможность не только установить равенство или неравенство между измеряемыми объектами, но и определить характер неравенства в виде логических суждений типа «больше и меньше», «хуже и лучше».
При помощи шкалы порядка можно измерять показатели, являющиеся качественными, но не имеющие строгих количественных мер. Широкое применение нашли такие шкалы в психологии и педагогике, а также социологии.
Шкала абсолютных величин
Часто величина чего-либо измеряется напрямую. К примеру, непосредственно подсчитывают количество дефектов в изделиях, число единиц выпущенной продукции, количество присутствующих на лекции студентов, сколько прожито лет и так далее. Делая такие измерения, на шкале отмечаются точные абсолютные количественные значения того, что измеряется. Шкала абсолютных значений имеет точно такие же свойства, что шкала отношений. Разница лишь в том, что те величины, которые обозначаются на первой, носят абсолютный, а не относительный характер.
Результаты, получаемые после измерения по данной шкале, обладают наибольшей достоверностью и информативностью. Они очень чувствительны к неточностям в измерениях.
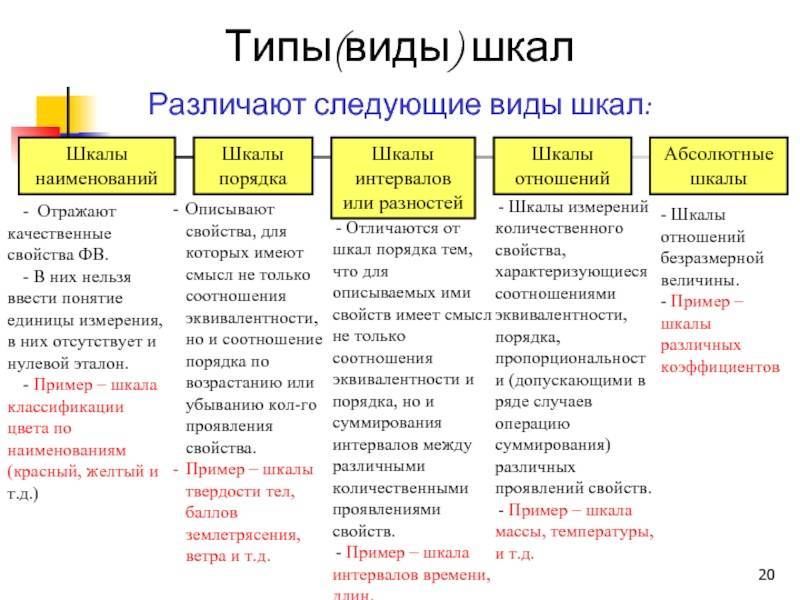
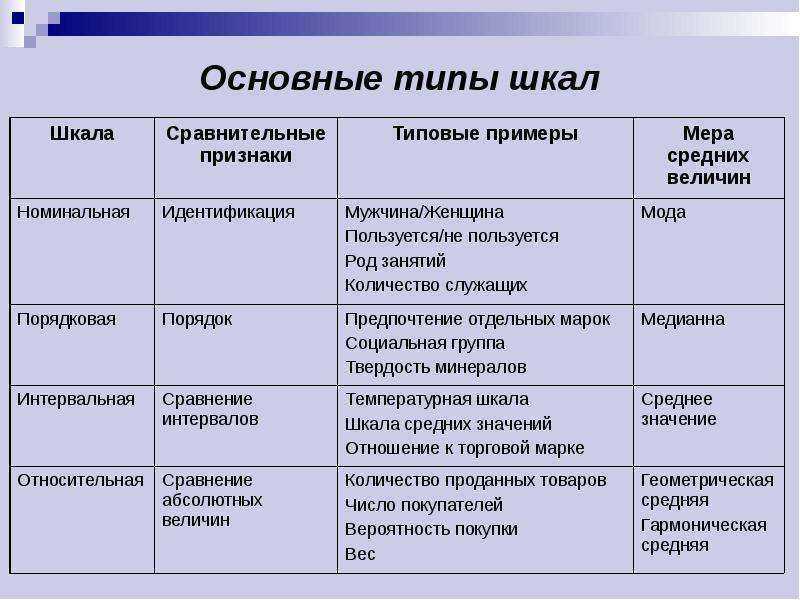
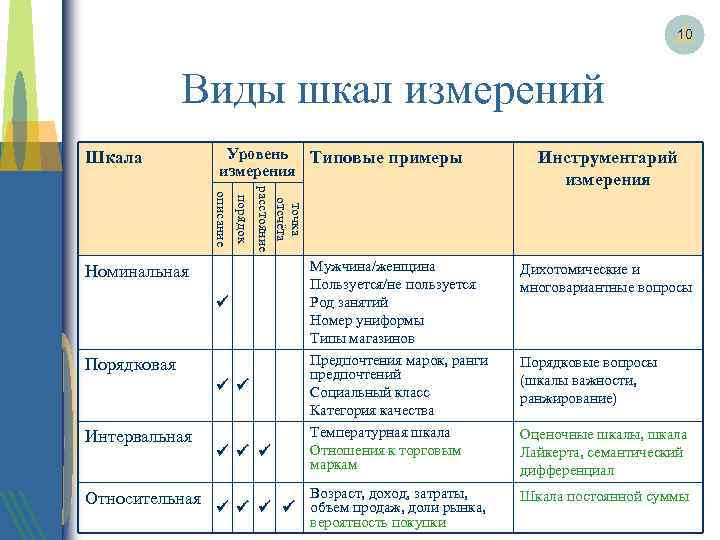
Типы шкал
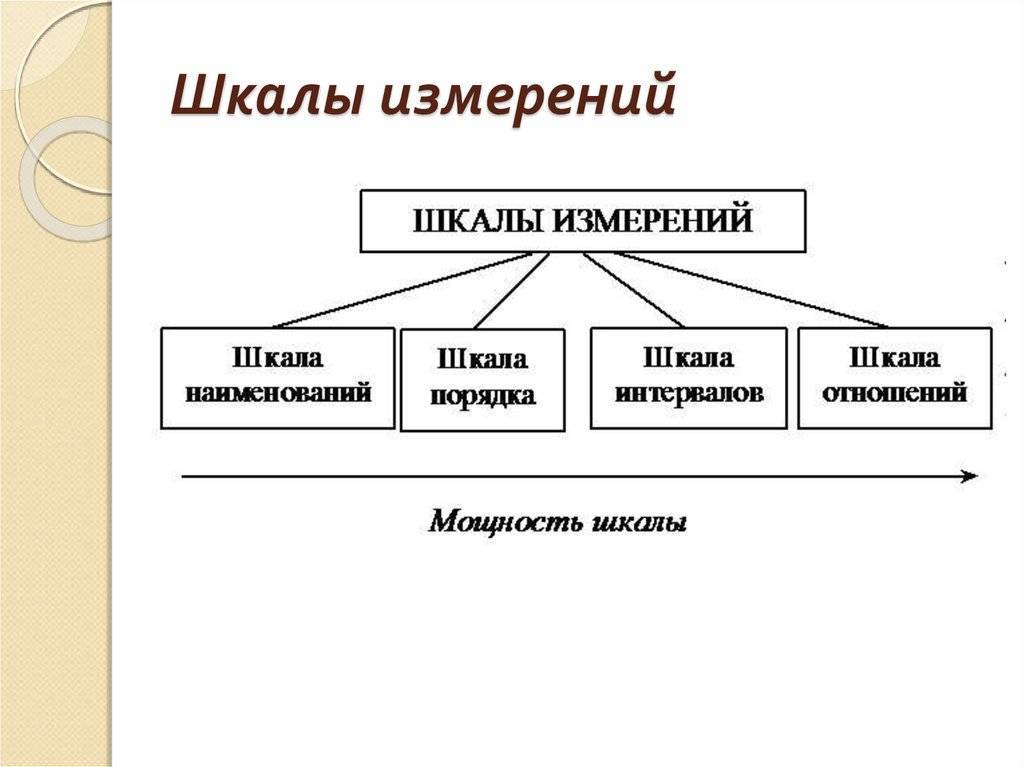
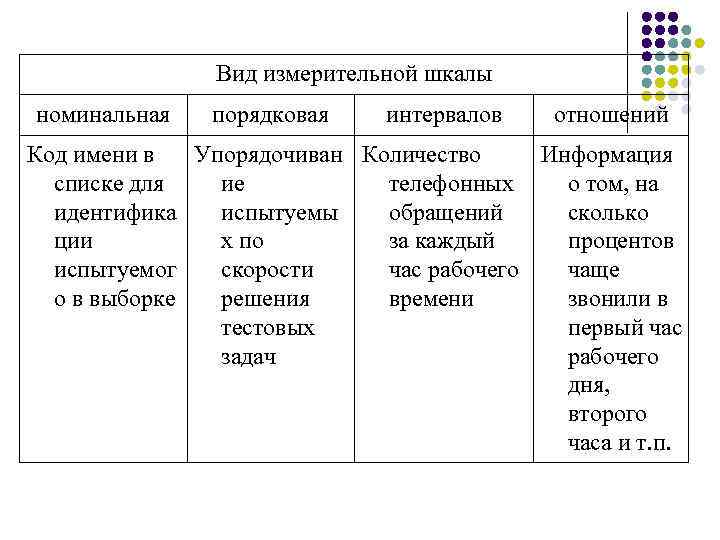
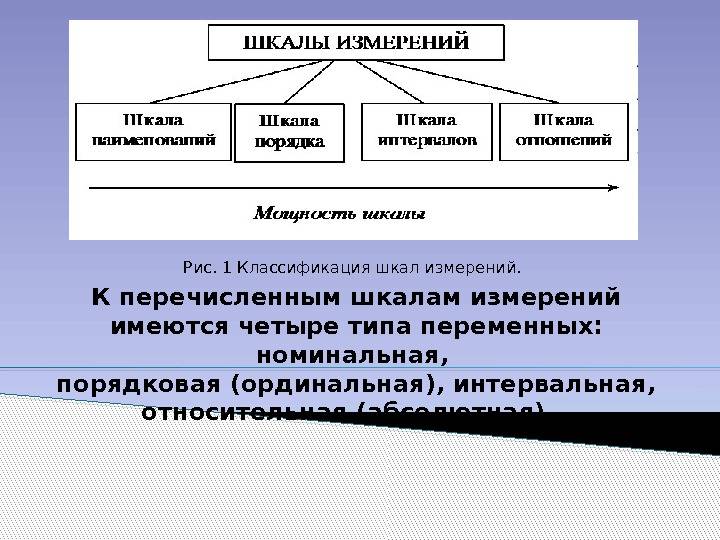
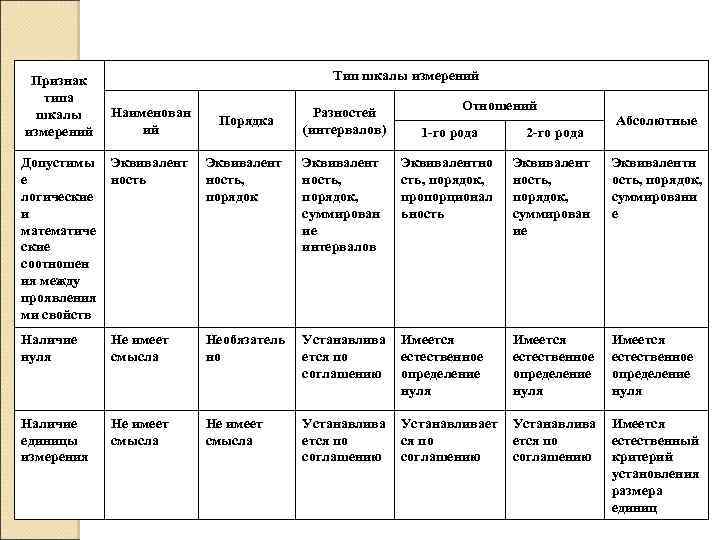
На сегодняшний день различают четыре основных типа шкал измерений: номинальная, порядковая, интервальная и относительная. Каждый тип шкалы обладает определенными признаками, которые рассматриваются ниже; сейчас же рассмотрим какую роль играет техника измерений в процессе классификации.
Часто при классификации исследователь не имеет возможности численно измерить исследуемый параметр. Например, отношение человека к чему-либо, степень его предпочтения и т.д. Способы измерения в данном случае отличаются от традиционных способов. Измерением в данном случае будет считаться любой способ приписывания числовых значений символам, которые отражают качественные характеристики объектов. При этом должны существовать устойчивые взаимосвязи между символами и качествами, которые они отражают. Иными словами, для осуществления кластеризации объекта с качественными характеристиками необходимо использовать приемы техники шкалирования.
В процессе использования техники шкал традиционно выделяют ряд стадий, качество выполнения которых оказывает непосредственное влияние на результат выделения кластеров. На первом этапе необходимо дать четкое определение тому, что собираются измерять. Далее следует указать, как измерение будет осуществлено на практике или что/кто конкретно подлежит измерению. После чего выбирают тип шкалы измерения, который предопределяет метод сбора информации. Любые измерения связаны с ошибками, но поскольку измерение в данном случае имеет специфику, то исследователь может самостоятельно оценить некоторые случайные отклонения исследуемого параметра и исключить его из кластера. Традиционно объекты наблюдения могут быть представлены в следующих типах шкал.
1 тип: номинальная или шкала наименований
Этот базовый и самый примитивный тип шкалы. При его использовании каждому объекту присваивается только идентификационный номер, как, например, номера игроков в спортивной команде, номера телефонов и т.д.
Операции в данной шкале:
2 тип: порядковая шкала
Этот тип шкалы определяет порядок или ранг объектов наблюдения. Расстояния между объектами, которые следуют друг за другом (по убыванию или по возрастанию) не являются равными. На основании результата ранжирования нельзя сказать, что расстояние между свойствами объектов и равны расстоянию между свойствами объектов и . Часто данный тип шкалы еще называют шкалой восприятия. Например, оценка качества вина по десятибалльной шкале – наиболее понравившееся качество 10 баллов, наименее – 1 балл.
Операции в данной шкале:
3 тип: интервальная шкала
В отличие от порядковой шкалы, здесь имеет значение не только порядок следования величин, но и величина интервала между ними. Пример для данного типа шкалы: температура воды в море утром – 18 градусов, вечером – 24, т.е. вечерняя на 5 градусов выше, но нельзя сказать, что она в 1.33 раз выше.
Операции, которые можно выполнять на базе этой шкалы:
4 тип: относительная или шкала отношений
В отличие от интервальной шкалы может отражать то, во сколько один показатель больше другого. Относительная шкала имеет нулевую точку, которая характеризует отсутствие измеряемого качества. Например: цена на товар. Здесь за точку отсчета можно взять «ноль» рублей. Отметим, что на практике не часто удается привести измерения к данному типу шкалы.
Операции для данной шкалы:
Шкалы и их классификации
Шкалы используются как для первичных измерений, так и для перевода разных измерений (в нашем случае — различных показателей) в единую шкалу. Как выбрать единую шкалу? Начнём с трёх определений.
Шкалой называют систему чисел или иных элементов и отношений между ними, принятых для измерения или оценки каких-либо величин (объектов, качеств и т. д.).
Шкалирование — это:
- выбор шкалы для первичных измерений;
- перевод измерения из одной шкалы в другую.
Нормирование (или единообразное шкалирование) — это перевод всех переменных, показателей, отражающих разные объекты измерений, в одну шкалу.
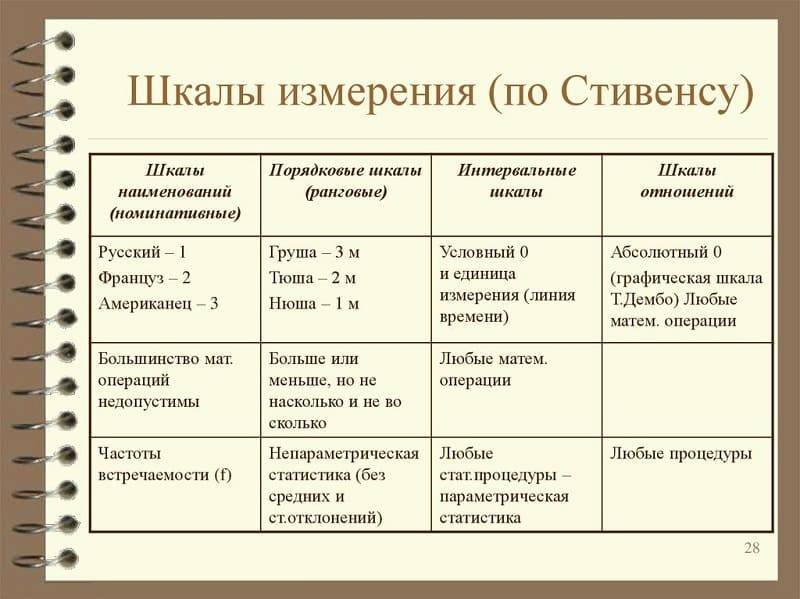
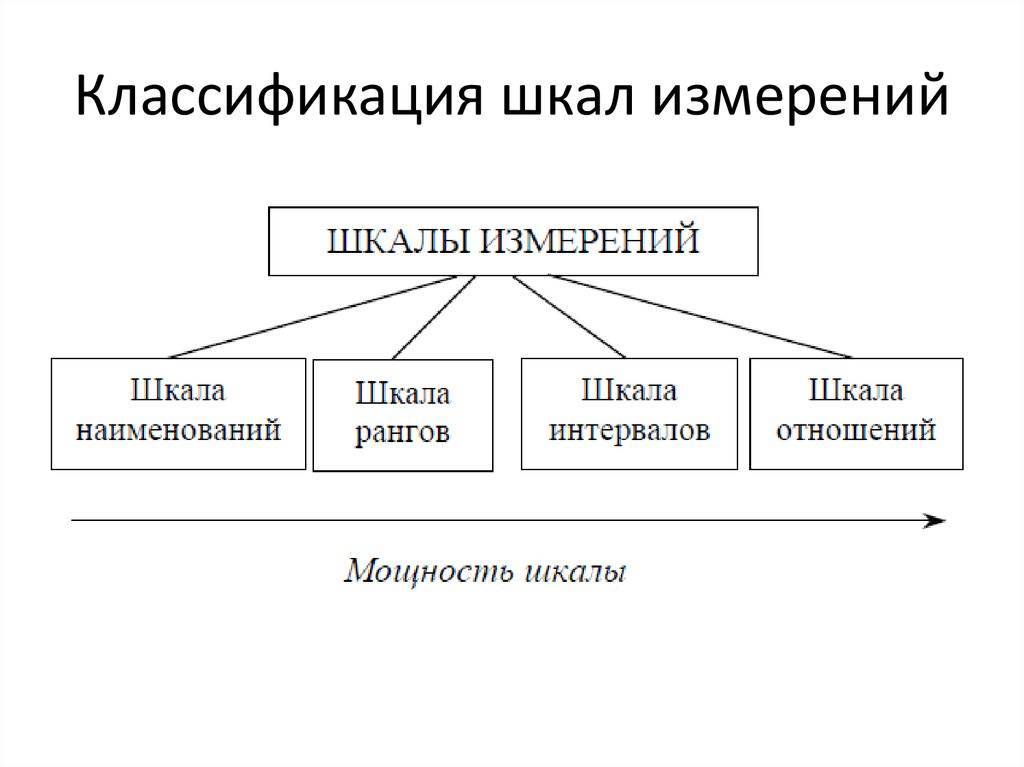
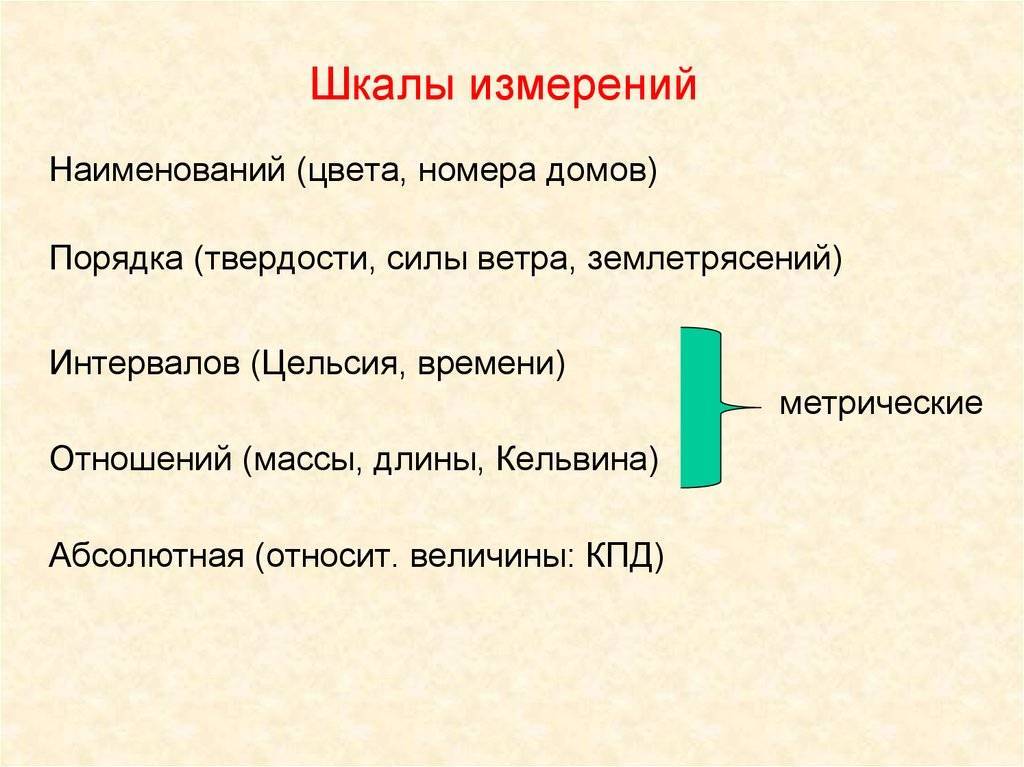
Первая классификация шкал была предложена С. Стивенсом в 1946 г. и от современной общепринятой классификации принципиально не отличается. Шкалы, как правило, объединяют в три основные группы:
- номинальные — для качественных измерений;
- порядковые — для отражения отношения порядка (больше, лучше, важнее, проще, правильнее и т. п.);
- количественные — оперируют с числами так, как мы привыкли со школьных времен (например, 10 в 2 раза больше, чем 5).
Иногда все шкалы измерения делят на два класса:
- шкалы качественных признаков (порядковая шкала и шкала наименований);
- шкалы количественных признаков (количественные шкалы).
Далее мы последовательно разберём все типы шкал.
Как считать очки в десятиборье?
Сегодня в мужском легкоатлетическом десятиборье за удачное выступление в каждом виде спорта участнику начисляется около 1000 очков. Но какой результат, по вашему мнению, берётся за 1000? Первое, что приходит на ум, — взять за 1000 очков мировой рекорд для женщин. Но какой именно? Текущий не годится, так как он меняется, а хотелось бы иметь возможность сравнений во времени и измерять рекорды. Но допустим, мы зафиксируем раз и навсегда, за что дается 1000 очков: в прыжках в длину, например, за 7,90 м, в беге на 100 метров — за 11 секунд. Далее возникает другой вопрос: какой шаг указать? Результат 8,00 м в прыжках в длину — это 1050 или 1010 очков? И как справедливо сравнивать разные виды соревнований? Думается, у каждого специалиста будут на этот счёт своё мнение и своя шкала.
Замечания (описание)
Выбор шкал измерения не является проектным методом в общепринятом смысле» однако, не прибегая к измерениям, невозможно применять четкую методологию проектирования. Принципы измерения имеют следующее отношение к проектированию:
а) Важнейшие измерения при проектировании те, которые непосредственно связаны с задачами и критериями проекта
Поскольку задачи и критерии лишь редко можно измерить с помощью привычной пропорциональной шкалы, очень важно уметь пользоваться менее широко известными шкалами низшего порядка. В книгах Холла, Кофмана и Зигеля подробно рассматриваются такие шкалы.
б) Для того чтобы понять некоторые из описанных в этой книге методов, требуется хотя бы элементарное знакомство с измерительными шкалами
Поэтому при обсуждении этих методов даются ссылки на манный раздел.
в) Инженеры, архитекторы и другие специалисты, для которых измерения имеют важное значение, как правило, не знают никаких измерительных шкал, кроме пропорциональных. В какой-то мере это объясняется тем, что задачи более высокого уровня, к которым применимы шкалы низшего порядка, традиционно решались на основании слыл и здравого смысла. В будущем их, однако, часто придется решать с помощью измерения и вычислений.
Зависимость вычислений от измерений и отношение точности к стоимости и величине штрафа редко освещаются в литературе, посвященной методам проектирования.
Следует иметь в виду, что на тщательные размышления и действия, связанные с выполнением точных и полезных для практики измерений, требуется значительно больше времени и сил, чем для проектирования «сидя в кресле» Поэтому приведенный выше пример следует рассматривать лишь как беглый набросок тех размышлений, которые необходимы для полного планирования соответствующих измерений. Подробное рассмотрение этих вопросов наняло бы добрую половину книги и явилось бы бесполезным описанием принципов, которые гораздо лучше описаны в книгах по математике и другим наукам
Единственный новый аспект описанной здесь методики — это объединение естественнонаучных, математических и экономических принципов в единую процедуру планирования измерении, которая связывает эти принципы с существенно важными вопросами проектирования.
Изложенная методика может показаться чересчур осторожной инженерам и всем, кому часто приходится применять вычисления по пропорциональным шкалам к ситуациям, которые могут быть точнее представлены более простыми или более сложными шкалами измерения, примером чему может служить использование интервальной шкалы для измерения многомерных показателей теплового комфорта (метод «Морфологические карты»). Конечно, результирующие ошибки, вызванные неправильным выбором шкалы, могут оказаться и небольшими
Однако трудно узнать заранее, так ли это на самом деле, и возможны случаи, когда погрешности будут велики. Например, при подаче небольшого количества тепла затраты на отопление комнаты слабо зависят от погрешностей при выборе шкалы комфорта, но при неограниченной подаче тепла эта зависимость может быть очень сильной.
Эта дилемма возникает также и при попытке определить порядок приоритетов при загрузке различных типов столовой посуды на этапе 4 приведенного примера. Этот вопрос рассматривается в методах «Ранжирование и взвешивание» и «Составление технического задания».
Использование в психометрии
Основная статья: Психометрия
Используя различные шкалы, можно производить различные психологические измерения. Самые первые методы психологических измерений были разработаны в психофизике. Основной задачей психофизиков являлось то, каким образом определить, как соотносятся физические параметры стимуляции и соответствующие им субъективные оценки ощущений. Зная эту связь, можно понять, какое ощущение соответствует тому или иному признаку. Психофизическая функция устанавливает связь между числовым значением шкалы физического измерения стимула и числовым значением психологической или субъективной реакцией на этот стимул.
Ответы
27+27=54логично
Объяснение:
ты серьезно?Зачем ты выложил пистолет?
я не знаю ей та в интернете поищи понял
Объяснение:
аж сори
Другие вопросы по Физике
Пловец прыгает в море со скалы высотой 20м. вычислить его скорость на высоте 15м над поверхностью моря. какая скорость пловца в момент входа в море? сопротивление воздуха не учитывать
Ответов: 3
Чему равно давление идеального газа, количество вещества которго 2 моль и который занимает 8.3 м в кубе при температуре 250 к ?
Ответов: 3
Пассажир поезда, идущего со скоростью 15 м/с, видит встречный аоезд длиной 150 м в тесение 6 с. какова при этом скорость встречного поезда?
Ответов: 1
При равномерном движении пешеход проходит за 10 с путь 15 м. какой путь он пройдёт при движении с той же скоростью за 2 с?
Ответов: 2
Сопротивление проволоки длиной 45 м. равно 180 ом . какой длины надо взять проволоку из такого же материала и той же площади поперечного сечения чтобы её сопротивление было 36 ом
Ответов: 1
Два тела равномерно движутся по окружностям одинакового радиуса. линейная скорость первого тела в 3 раза больше линейной скорости второго тела. во сколько раз центростремительное ускорение первого тела больше центростремительного ускорение второго тела?
Ответов: 2
Знаешь правильный ответ?
существуют различные шкалы для измерения расстояний так метрическая шкала распространена в Европе и…
Вопросы по предметам
Алгебра, 05.09.2021 16:49
Математика, 05.09.2021 16:49
Математика, 05.09.2021 16:49
Русский язык, 05.09.2021 16:49
Математика, 05.09.2021 16:49
Геометрия, 05.09.2021 16:49
Математика, 05.09.2021 16:49
Интервальная шкала
Интервальная шкала обладает метрическими свойствами — она характеризуется значением интервала и допускает арифметическое сложение.
Интервальные шкалы часто называют шкалами высокого типа, количественными, числовыми. Смысл таких определений очевиден: числа, полученные с помощью шкал высокого типа, больше похожи на те числа, которые знакомы каждому из нас со школьной скамьи.
Интервальная шкала обладает также характеристикой расстояния между отдельными градациями шкалы, измеряемого с помощью определенной единицы измерений. На этой шкале оцениваются разности между отдельными градациями шкалы и можно решить, равны они или нет, а если не равны, то какая из двух больше.
Интервальная шкала обладает также характеристикой расстояния между отдельными градациями шкалы, измеряемого с помощью определенной единицы измерений, то есть используется количественная информация. На этой шкале уже не бессмысленны разности между отдельными градациями шкалы. В данном случае можно решить, равны они или нет, а если не равны, то какая из двух больше.
Они представляют собой интервальные шкалы с естественным началом.
Простейшим примером интервальной шкалы может служить шкала измерения температуры по Цельсию.
При использовании интервальной шкалы адекватным является сравнение расстояний между парами одной и той же системы.
Непрерывный континуум интервальной шкалы позволяет рассчитывать средневзвешенные величины, коэффициент дисперсии, характеризующий степень разбросанности признака. При этом средневзвешенные величины используются в качестве разного рода индексов, выполняющих функцию классификации, измерения и сравнения.
Условием применения интервальной шкалы является регулярность классов интервалов.
Если в интервальной шкале масштаб зафиксирован, то измерение происходит в шкале разностей. Шкала разностей допускает операции равенство-неравенство, больше-меньше, равенство-неравенство интервалов и операцию вычитания, на основе которой устанавливается величина интервала в фиксированном масштабе. К шкале разностей относятся логарифмические шкалы, а также процентные и аналогичные им шкалы измерений, задающие безразмерные величины.
Измерения в интервальных шкалах в известном смысле более совершенны, чем в порядковых. Применение этих шкал дает возможность не только упорядочить объекты по количеству свойства, но и сравнить между собой разности количеств.
Это справедливо для любых интервальных шкал.
Если начало в интервальной шкале является абсолютной нулевой точкой, то возникает возможность отразить в шкале, во сколько раз одно измерение отличается от другого. Соответствующая шкала называется шкалой отношений.
| Частично-упорядоченное множество типов шкал, наиболее часто использующихся в социологических. |
Наиболее типичные способы получения интервальной шкалы фактически описаны выше.
Шкалы измерений
Номинальная шкала
В шкале наименований допустимыми являются все взаимно-однозначные преобразования. В этой шкале числа используются как метки, только для различения объектов. В шкале наименований измерены, например, номера телефонов, автомашин, паспортов, студенческих билетов. Пол людей тоже измерен в шкале наименований, результат измерения принимает два значения – мужской, женский. Очевидно, что не имеет смысла складывать номера телефонов или умножать серии паспортов.
КДП: биективные преобразования.
Порядковая шкала
В порядковой шкале числа используются не только для различения объектов, но и для установления порядка между объектами. Простейшим примером являются оценки знаний учащихся. Заметим, что в средней школе применяются оценки 2, 3, 4, 5, а в высшей школе ровно тот же смысл выражается словесно – неудовлетворительно, удовлетворительно, хорошо, отлично. Этим подчеркивается “нечисловой” характер оценок знаний учащихся. В порядковой шкале допустимыми являются все строго монотонные преобразования.
КДП: все строго монотонные преобразования.
Шкала интервалов
По шкале интервалов измеряют величину потенциальной энергии или координату точки на прямой. В этих случаях на шкале нельзя отметить ни естественное начало отсчета, ни естественную единицу измерения. Исследователь должен сам задать точку отсчета и сам выбрать единицу измерения. Допустимыми преобразованиями в шкале интервалов являются линейные возрастающие преобразования, т.е. линейные функции. Температурные шкалы Цельсия и Фаренгейта связаны именно такой зависимостью: °C = 5/9 (°F – 32), где °C – температура (в градусах) по шкале Цельсия, а °F – температура по шкале Фаренгейта.
КДП: все преобразования вида
Шкала отношений
В шкалах отношений есть естественное начало отсчета – нуль, но нет естественной единицы измерения. По шкале отношений измерены большинство физических единиц: масса тела, длина, заряд, а также цены в экономике. Допустимыми преобразованиями шкале отношений являются подобные (изменяющие только масштаб). Другими словами, линейные возрастающие преобразования без свободного члена. Примеры использования таких преобразований: пересчет цен из одной валюты в другую по фиксированному курсу, перевод массы из килограмм в фунты.
КДП: все преобразования вида
Шкала разностей
В шкале разностей есть естественная единица измерения, но нет естественного начала отсчета. Время измеряется по шкале разностей, если год (или сутки – от полудня до полудня) принимаем естественной единицей измерения, и по шкале интервалов в общем случае. На современном уровне знаний естественного начала отсчета времени указать нельзя. Допустимыми преобразованиями шкале разностей являются сдвиги.
КДП: все преобразования вида
Абсолютная шкала
Только для абсолютной шкалы результаты измерений – числа в обычном смысле слова. Примером является число людей в комнате. Для абсолютной шкалы допустимым является только тождественное преобразование.
КДП:
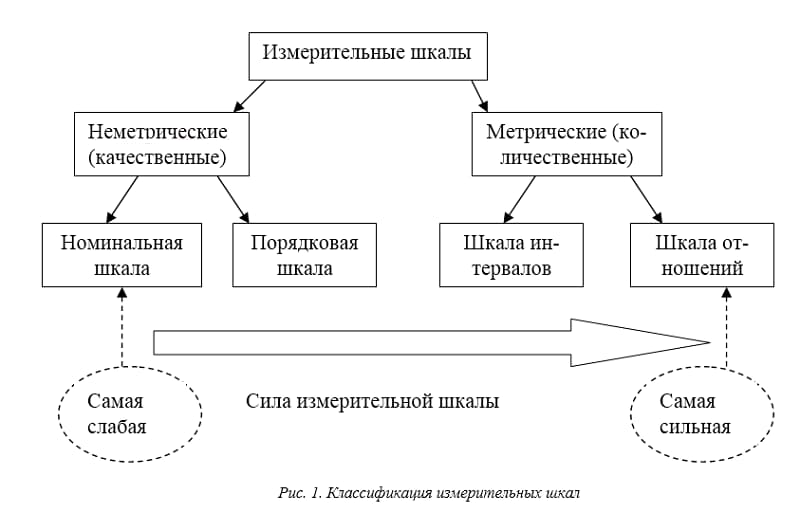
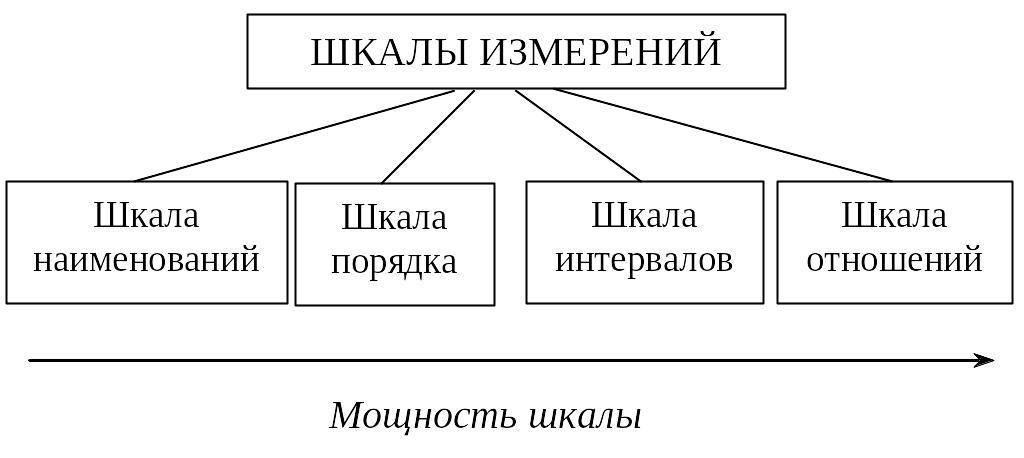
Иерархия шкал измерений
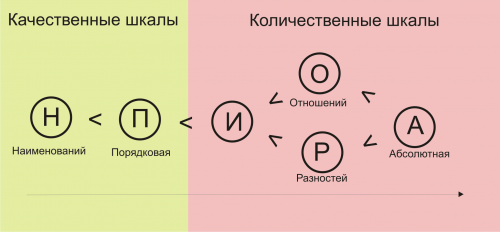Иерархия шкал измерений. Слева – самая слабая шкала, справа – самая сильная.
Все шкалы делят также на 2 большие группы: качественные и количественные. К качественным шкалам относят номинальную и порядковую, к количественным – все остальные. Это разделение показывает разницу в природе шкал: например, невозможно утверждать, что школьная оценка 2 настолько же хуже оценки 4, насколько 3 хуже оценки 5, поэтому порядковые шкалы относят к качественным. В то же время, для тел разной массы аналогичное утверждение корректно: тело массой 5 кг настолько же тяжелее тела массой 3 кг, насколько тело массой 4 кг тяжелей тела массой 2 кг. Таким образом, шкалы отношений – это количественные шкалы.
Очевидно, что КДП одной шкалы может полностью включать в себя КДП другой. Тогда говорят, что вторая шкала сильнее первой. На иллюстрации изображена иерархия шкал.
Меры веса
Массой называют величину, которая обозначает, сколько вещества содержит тело. В обиходе масса получила название вес. Часто при взвешивании говорят: «Вес этого вещества (материала, предмета) такой-то». Но на самом деле это не вес, а масса данного тела.
Таким образом, масса и вес — не одно и то же. Весом называют силу, которую тело прилагает к горизонтальной опоре. Вес измеряют в ньютонах. Масса же как величина отражает количество.
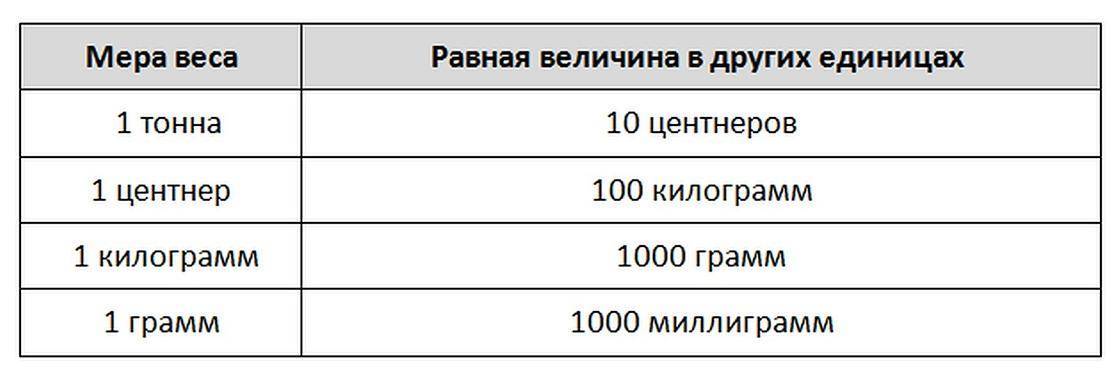
Как же выразить значение массы и что для этого надо знать? Основные единицы измерения массы таковы:
Существует ли машина времени в действительности?
- Самая маленькая единица — миллиграмм (мг). Миллиграммы редко применяются на практике. Их используют химики и другие ученые, работа которых связана с маленькими количествами веществам. В обычной жизни редко отмеряем что-либо миллиграммами.
- Следующей единицей стал грамм (г). В граммах часто измеряют количество продуктов, когда составляют рецепты. Один грамм состоит из тысячи миллиграммов. Между этими величинами ставят знак равенства, так как они тождественны: 1 г = 1000 мг.
- Следующая единица — килограмм (кг). Это общепринятая единица измерения в мире, включенная в международную систему. Один килограмм содержит тысячу граммов, то есть: 1 кг = 1000 г.
- За килограммом следует центнер (ц). В центнерах измеряется масса урожая, который собирают с небольших участков или масса различных грузов. Один центнер — это сто килограммов (1 ц = 100 кг).
- Тонна (т) — самое большое значение, с которым сталкиваются школьники, когда изучают массу предметов. Тонны используют, чтобы измерить большой груз и массу больших тел, таких как космические корабли или автомобили. Одна тонна состоит из тысячи килограмм (1 т = 1000 кг).
Знаки зодиака по числам рождения
Если обобщить представленную выше информацию, то для измерения массы существует:
Свойства шкал
Неравномерная шкала омметра
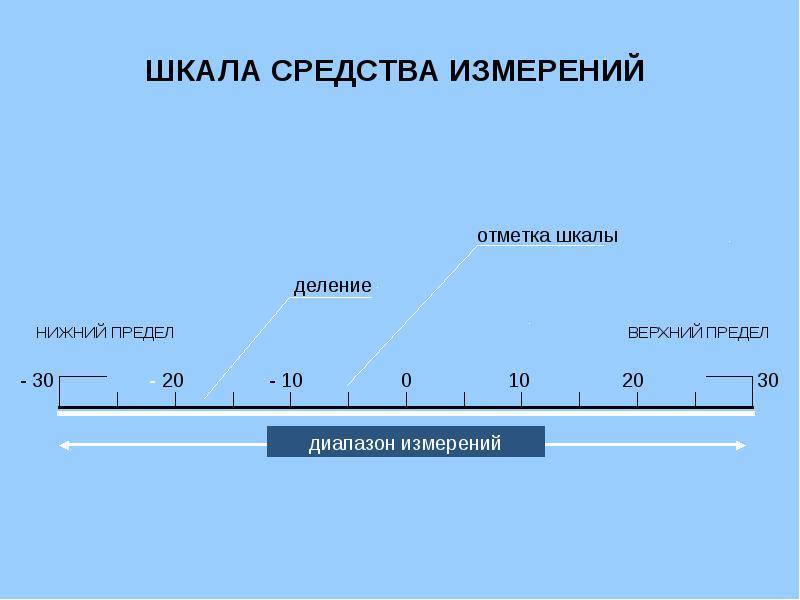
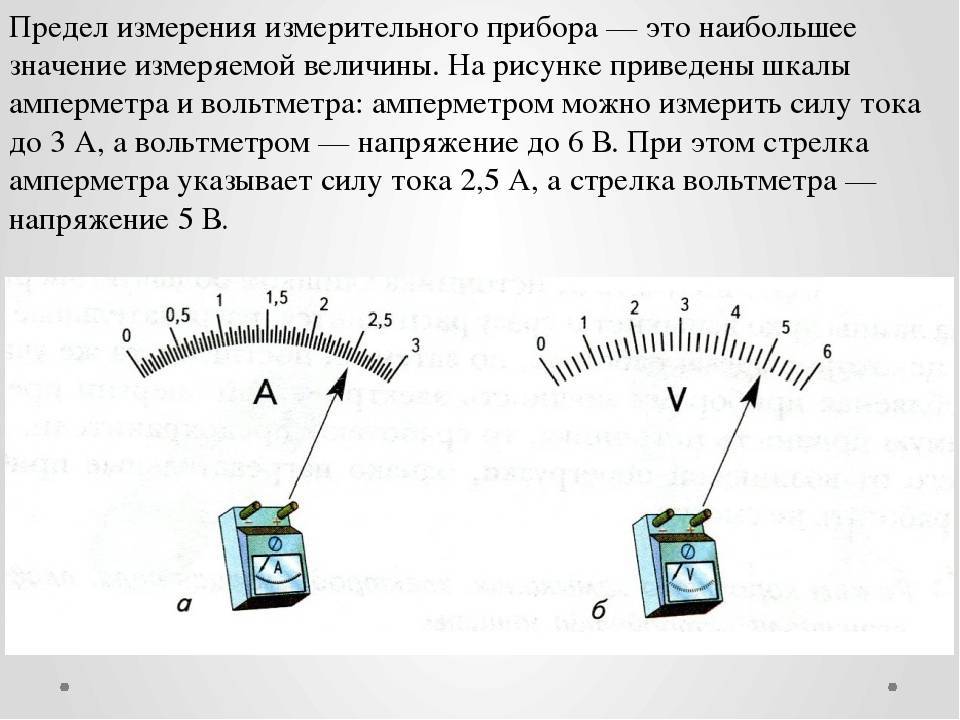
- Начальное значение шкалы — наименьшее значение измеряемой величины, которое может быть отсчитано по шкале средства измерений. Во многих случаях шкала начинается с нулевой отметки, однако могут быть и другие значения — например, у медицинского термометра это 34,3 °C.
- Конечное значение шкалы — наибольшее значение измеряемой величины, которое может быть отсчитано по шкале средства измерений.
- Характер шкалы — функциональная зависимость a = f(x) между линейным (или угловым) расстоянием a какой-либо отметки от начальной отметки шкалы, выраженным в долях всей длины шкалы, и значением x измеряемой величины, соответствующим этой отметке:
- Равномерная шкала — шкала, отметки на которой нанесены равномерно.
- Неравномерная шкала — шкала, отметки на которой нанесены неравномерно.
- Логарифмическая или гиперболическая шкала — шкала с сужающимися делениями, характеризуемыми тем, что отметка, соответствующая полусумме начального и конечного значений, расположена между 65 и 100 % длины шкалы. Следует заметить, что выражение «логарифмическая шкала» используется и по отношению к другому значению понятия «шкала» (см.: Шкала физической величины, Логарифмический масштаб).
- Степенная шкала — шкала с расширяющимися или сужающимися делениями, но не подпадающая под определение логарифмической (гиперболической) шкалы.
Шкала интервалов (разностей)
Эти шкалы измерений в метрологии являются дальнейшим развитием шкал порядка и применяются для объектов, свойства которых удовлетворяют отношениям эквивалентности, порядка и аддитивности. Шкала интервалов состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало – нулевую точку. Пример шкалы интервалов — летоисчисление по различным календарям, в которых за начало отсчета принято либо сотворение мира, либо рождество Христово и т.д. Температурные шкалы Цельсия, Фаренгейта и Реомюра также являются шкалами интервалов.
Рисунок – Пример шкалы интервалов (Температурные шкалы Цельсия и Фаренгейта)
На шкале интервалов определены действия сложения и вычитания интервалов. Действительно, по шкале времени интервалы можно суммировать или вычитать и сравнивать, во сколько раз один интервал больше другого, но складывать даты каких-либо событий просто бессмысленно.
Шкала интервалов величины Q описывается уравнением Q = Qо + q, где q — числовое значение величины; Qо — начало отсчета шкалы; — единица рассматриваемой величины. Такая шкала полностью определяется заданием начала отсчета Qо шкалы и единицы данной величины .
Задать шкалу практически можно двумя путями. При первом из них выбираются два значения Qо и Q1, величины, которые относительно просто реализованы физически. Эти значения называются опорными точками, или основными реперами, а интервал (Q1 ~ Qо) — основным интервалом. Точка Qо принимается за начало отсчета, а величина (Q1 -Qо)/n= за единицу Q. При этом n выбирается таким, чтобы было целой величиной.
Рисунок – Пример шкалы отношений
При втором пути задания шкалы единица воспроизводится непосредственно как интервал, его некоторая доля или некоторое число интервалов размеров данной величины, а начало отсчета выбирают каждый раз по-разному в зависимости от конкретных условий изучаемого явления. Пример такого подхода — шкала времени, в которой 1с = 9192631770 периодов излучения, соответствующих переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133. За начало отсчета принимается начало изучаемого явления.
Шкала отношений
Шкала отношений описывает свойства эмпирических объектов, которые удовлетворяют отношениям эквивалентности, порядка и аддитивности (шкалы второго рода — аддитивные), а в ряде случаев и пропорциональности (шкалы первого рода — пропорциональные). Пример шкалы отношений — шкала массы (второго рода), термодинамической температуры (первого рода).
В шкалах отношений существует однозначный естественный критерий нулевого количественного проявления свойства и единица измерений, установленная по соглашению. С формальной точки зрения этот вид шкал измерений является шкалой интервалов с естественным началом отсчета
К значениям, полученным по этой шкале, применимы все арифметические действия, что имеет важное значение при измерений физических величин
Рисунок – Пример абсолютной шкалы (шкала температур Кельвина)
Шкалы отношений — самые совершенные. Они описываются уравнением Q = q, где Q — ФВ, для которой строится шкала, — ее единица измерения, q — числовое значение ФВ. Переход от одной шкалы отношений к другой происходит в соответствии с уравнением q2 = q1/.
2.2. Условия упорядоченности
Номера так же, как и числа, упорядочены; первые — произвольные образом, вторые — на основании двух отношений, существующих между упорядоченными объектами, — отношений, специальное название которых транзитивность и антисимметричность.
Транзитивность — если А находится в некотором отношении к В, а В к С, то А находится в том же отношении к С.
Симметричность — если А находится в некотором отношения к В, то В находится в том же отношении к А.
Антисимметричность — если А больше В, то В меньше А.
Отношение порядка применимо к свойству твердости: все тела, к которым применимо это понятие, связаны между собой транзитивным и антисимметричным отношением „тверже, чем» или обратным отношением „мягче, чем»; каждое тело, твердость„которого мы хотим определить, либо тверже любого другого тела того же класса, либо мягче него.
Отношение „тверже, чем» является транзитивным и антисимметричным.
Оно транзитивно потому, что если Аоставляет царапину на В, а В — на С, то Аоставляет царапину на С.
Оно антисимметрично потому, что если Аоставляет царапину на В, то Вне оставляет царапину на А.
Как научиться
Освоить принципы измерения достаточно легко, но они почти неизвестны инженерам и тем специалистам, в задачу которых входит давать точные ответы на поставленные вопросы. Те, кто не знаком с описанными шкалами измерения, могут прочитать книги Холла, Кофмана и Зигеля, а затем перейти к более специальной литературе. Лишь после этого следовало бы приступать к измерениям, могущим иметь важные последствия.
Возможно, что удастся избежать многих дорогостоящих ошибок и излишних затрат на проведение измерений с ненужной степенью точности, если лица, специально занимающиеся измерениями, ознакомятся с часто оставляемыми без внимания принципами измерений и с теорией ошибок.
Примечания
- Журавлев Ю.И., Рязанов В. В., Сенько О. В. «Распознавание». Математические методы. Программная система. Практические применения. — М.: Фазис, 2006. ISBN 5-7036-0108-8.
- ↑ Анфилатов В. С., Емельянов А. А., Кукушкин А. А. Системный анализ в управлении. — М. Финансы и статистика, 2002. — 368 с.
- Перегудов Ф. И., Тарасевич Ф. П. Введение в системный анализ. — М.: Высшая школа, 1989. — 367 с.
- ↑ Бахрушин В.Є. Методи аналізу даних. — Запоріжжя, КПУ, 2011
- ↑
- Mosteller, Frederick. Data analysis and regression : a second course in statistics (англ.). — Reading, Mass: Addison-Wesley Pub. Co, 1977. — ISBN 978-0201048544.
- Wolman, Abel G. Measurement and meaningfulness in conservation science (англ.) // Conservation biology : journal. — 2006.
- . Institute for Digital Research and Education. University of California, Los Angeles. Дата обращения: 7 февраля 2016.
- Суппес П., Зиннес Д. Основы теории измерений // Психологические измерения. М.: 1967. С. 9-110.
Шкалы измерений
Рассмотрим шкалы измерений подробнее.
Номинальная
Самые простые измерительные шкалы – номинальные. Они относятся к качественным и отражают те или иные свойства объекта, выраженные словесно. Их элементы могут только совпадать или не совпадать друг другом, Их нельзя сопоставлять по принципу «больше-меньше». Недопустимы также и арифметические действия.
Характерным примером может служить группа крови. Первая группа не больше третьей и не может быть сложена с четвертой. У человека может быть только одна группа крови, и измерение
Порядковая
По ней можно ранжировать и сравнивать объекты, по какому — либо признаку, например, расположить людей в строю по росту. Иванов больше Сидорова, а Сидоров больше Кузнецова.
Шкала порядка
Из этих данных можно сделать вывод о том, что Иванов выше Кузнецова, но нельзя определить, насколько именно.
Интервалов
Она состоит из заранее определенных и равных между собой интервалов. И является намного более информативной. Свойство объекта соотносится с одним из таких интервалов.
Характерным примером такой шкалы измерений может служить принятое у людей исчисление времени. Период оборота Земли вокруг Солнца делится на 365 дней, дни делятся на часы, далее на минуты и секунды. Мы можем соотнести событие с одним из таких интервалов: «эта статья была написана в 2018 году» или «Дождь начнется в 14 часов»
Шкалы интервалов
Значения в этом случае можно сравнивать друг с другом не только качественно, но и количественно, становятся доступны операции сложения и вычитания. «Заход солнца произойдет на 12 часов позже восхода». «Фильм А длиннее фильма В на 25 минут»
Однако поскольку начало отсчета не установлено, невозможно определить, во сколько раз одно значение больше другого.
Отношений
Точкой начала отсчета является точка, в которой значение параметра равно нулю. Появляется возможность отсчитывать от нее абсолютное значение параметра, определять разницы значений и во сколько раз одно больше другого. Характерный пример — температурная шкала Кельвина. За начало отчета взята точка «абсолютного нуля», при которой прекращается тепловое движение материи. Второй опорной точкой выбрана температура таяния льда при нормальном давлении. Разница между этими точками по Цельсию составляет 273 °C, и один градус Кельвина равен одному градусу Цельсия. Таким образом, можно сказать, что лед тает при 273К.
Шкала отношений
Отношений – наиболее информативная. На ней возможны все арифметические операции-
- сложение;
- вычитание;
- умножение ;
- деление.
Деление, умножение сложение и вычитание значений параметра будет иметь физический смысл. Мы можем вычислить не только насколько одно значение больше другого, но и во сколько раз.
Разностей
Представляет собой частный случай интервальных. Для них значение не меняется при произвольном числе сдвигов на определенный параметр. Другими характерными признаками являются
- единицы измерений и точка отсчета определяется по соглашению;
- существует понятие размерности;
- доступны операции линейных преобразований;
- осуществляется путем создания системы эталонов.
В качестве примера можно привести циферблат часов – каждые сутки значение времени будет, например, «7 часов», хотя это разные дни.
Циферблат часов
Другим примером может служить компас, показывающий направление из одной точки. Сама эта точка может иметь различные координаты.
Важно помнить, что в этом случае при измерении мы можем вычислять разницу между двумя значениями, но должны все время помнить о том, что начальное значении задано произвольно. Например, при переходе на летнее время придется задать новое начальное значение
Абсолютная
Абсолютная шкала занимает высшую ступень в шкальной иерархии. Единицы их естественные и не основаны на соглашениях и допущениях. Кроме того, эти единицы не имеют размерности, не служат производными системы СИ или какой-либо другой. Они всегда безразмерны:
- разы;
- проценты;
- доли;
- полные углы.
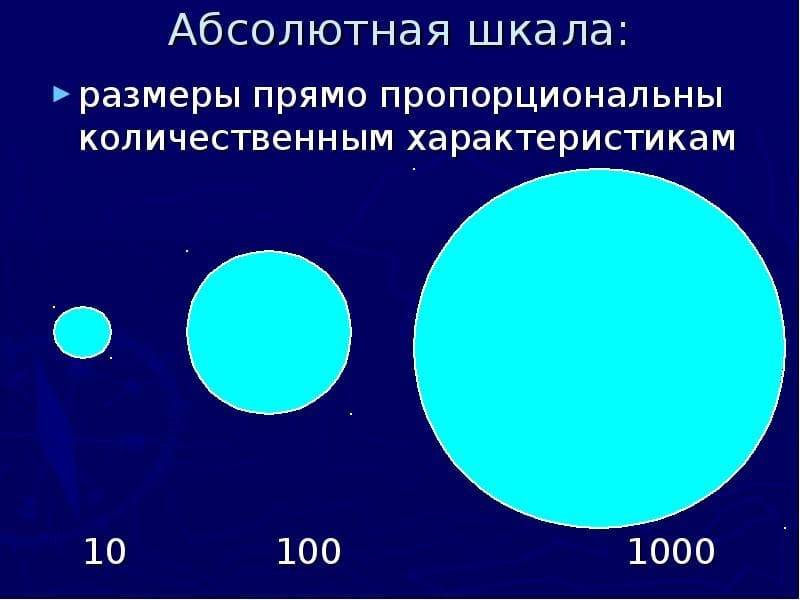
Абсолютная шкала
Абсолютные подразделяют на
- ограниченные. Диапазон от 0 до 1. Сюда относятся КПД, оптические коэффициенты поглощения т.д.
- неограниченные – предел упругости, коэффициент усиления в радиотехнике и т.д. Все они нелинейные и не имеют единиц измерений.
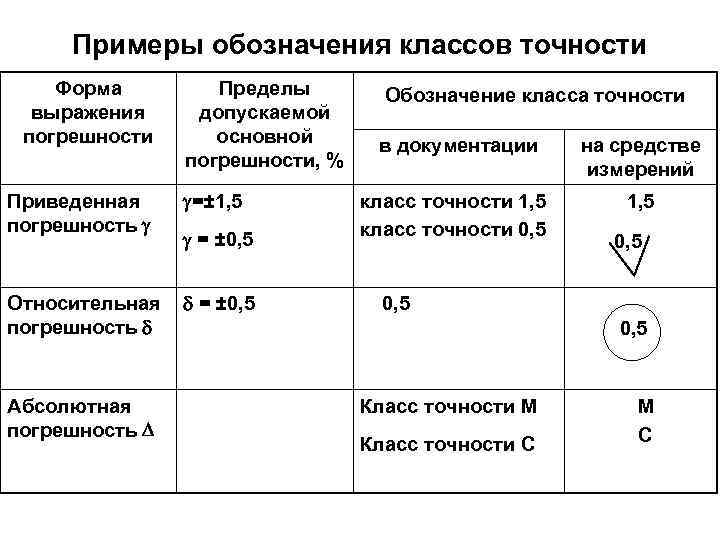
Итоги
Главной целью анализа цветов с помощью шкалы цветов являет измерение загрязнений, содержащихся в образце. Однако анализируемый цвет вещества не является достаточной информацией, позволяющей идентифицировать загрязнение и оценить качество изделия. Дополнительным параметром является результат измерения затуманенности. Некоторые спектрофотометры оснащены элементами, позволяющими проводить измерения затуманенности и цвета, что позволяет постоянно контролировать качество продукции. Поэтому спектрофотометры входят в число приборов, широко распространенных в лабораториях контроля качества.
