Чертежи зубчатого колеса

Классификация

По направлению витка передачи в большинстве своем бывают правыми. Иногда встречается левое направление нити.

Червячные зацепления классифицируются по форме наружной поверхности червяка:

• цилиндрические;
• глобоидные.

Вогнутая поверхность ведущей детали увеличивает количество зубьев, находящихся одновременно в зацеплении. В результате возрастает КПД и мощность передачи. Недостаток глобоидных червяков в сложности изготовления. Витки должны быть одинаковой высоты при вогнутой наружной поверхности.

По форме нити резьбы различают червяки:

• архимедов;
• конволютный;
• нелинейный.

Архимедов червяк отличается прямой в сечении эвольвентой. У конволютного конфигурация выпуклая, близкая к форме обычной шестерни. Нелинейные профили имеют выпуклую и вогнутую поверхность.

Зубчатое колесо имеет зуб наклонный обратной конфигурации, по форме совпадающий с впадиной между нитями.

Расположение червяка относительно колеса может быть:

• верхнее;
• боковое;
• нижнее.

Верхнее оптимально подходит для скоростных передач. Боковое наиболее компактное. При картерном способе смазки – масло находится в поддоне и нижняя деталь, вращаясь, смазывает остальные, удобнее нижнее расположение червяка.

Червячные колеса относятся к косозубым. Оси деталей располагаются обычно под углом 90°. В сильно нагруженных механизмах угол может быть 45°.

Зубчатые колеса по профилю зуба делят:

• роликовые;
• вогнутые;
• прямые.

По типу они могут быть:

• с непрерывным вращением – полные;
• зубчатый сектор.

Сектор может быть разной величины, от половины круга, до рабочей длины короче червяка.

Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Расчет модуля зубчатого колеса

Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

π×D=t×z,

проведя преобразование, получим:

D=(t /π)×z

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

t/π=m,

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

В=m×z;

выполнив преобразование, находим:

m=D / z.

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов D_e получается равным

De=d+2× h’,

где h’- высота головки.

Высоту головки приравнивают к m:

 h’=m.

Проведя математические преобразования с подстановкой, получим:

De=m×z+2m = m(z+2),

откуда вытекает:

m=De/(z+2).

Диаметр окружности впадин D_i соответствует D_e за вычетом двух высот основания зубца:

D_i=D-2h“,

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

h’ = 1,25m.

Устройство зубчатого колеса

Выполнив подстановку в правой части равенства, имеем:

D_i = m×z-2×1,25m = m×z-2,5m;

что соответствует формуле:

D_i = m(z-2,5m).

Полная высота:

h = h’+h“,

и если выполнить подстановку, то получим:

h = 1m+1,25m=2,25m.

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины s_в, получаем формулы для ширины впадины

• для отлитых зубцов: s_в=πm-1,53m=1,61m:
• для выполненных путем фрезерования- s_в= πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

Основные параметры

При изготовлении и применении колесных пар важное значение имеют параметры их составляющих. К основным параметрам относятся:

• Делительная окружность. Это те части элементов, которые соприкасаются между собой и катятся одна по другой без скольжения.
• Шаг – расстояние между профильными поверхностями соседних зубьев.
• Модуль (длина делительной окружности).
• Высота делительной головки.
• Диаметр окружности в районе вершин и на точках впадин зубьев.

Эти и другие параметры зубчатой передачи в обязательном порядке отображаются на чертежах. Их выбор зависит от назначения механизма, в котором будет использована зубчатая передача.

Большинство параметров инженеры рассчитывают во время проектирования, другие используют в готовом виде, выбирая их по специальным утвержденным таблицам.

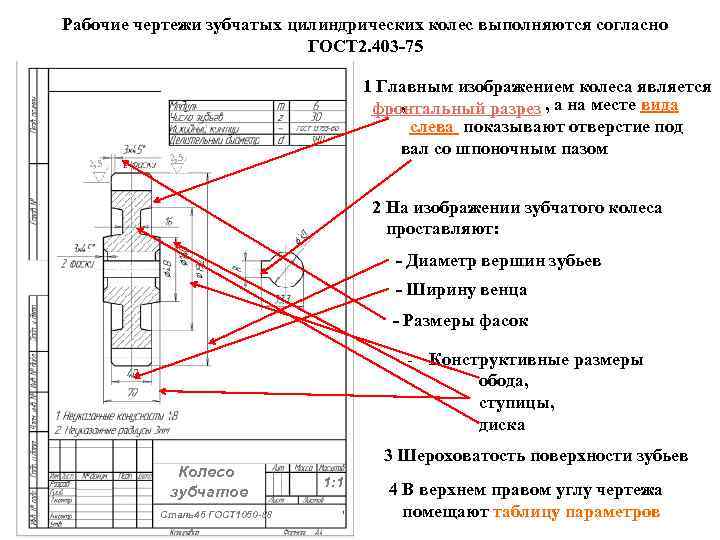
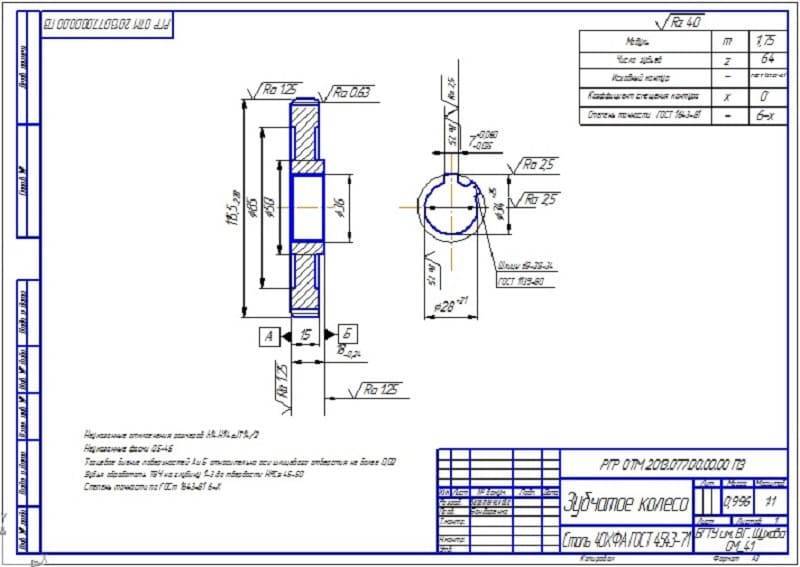
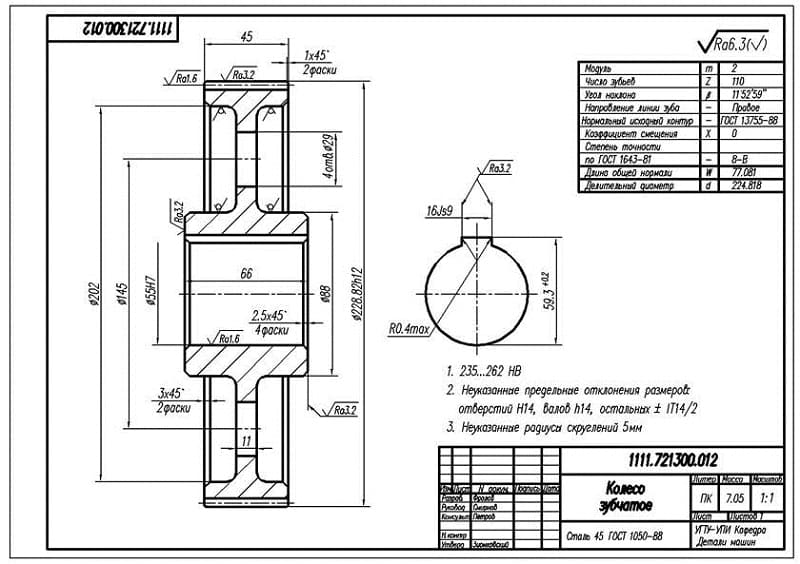
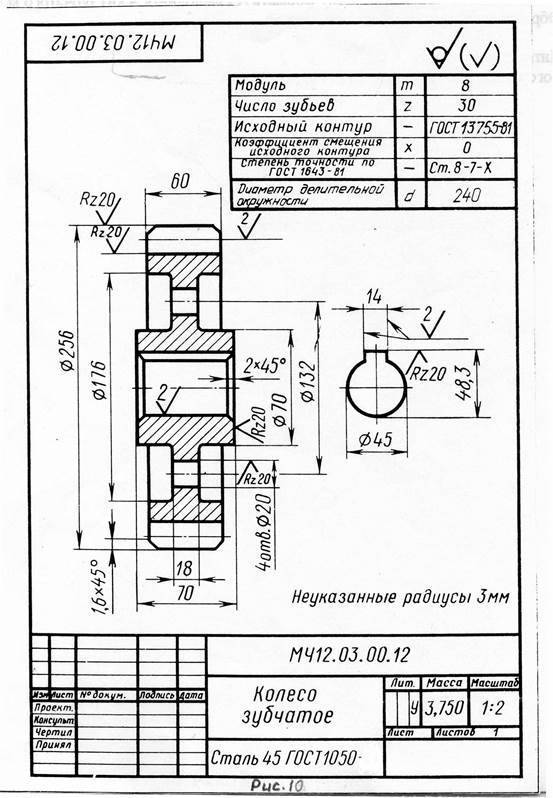
9.9. Выполнение чертежа зубчатого колеса

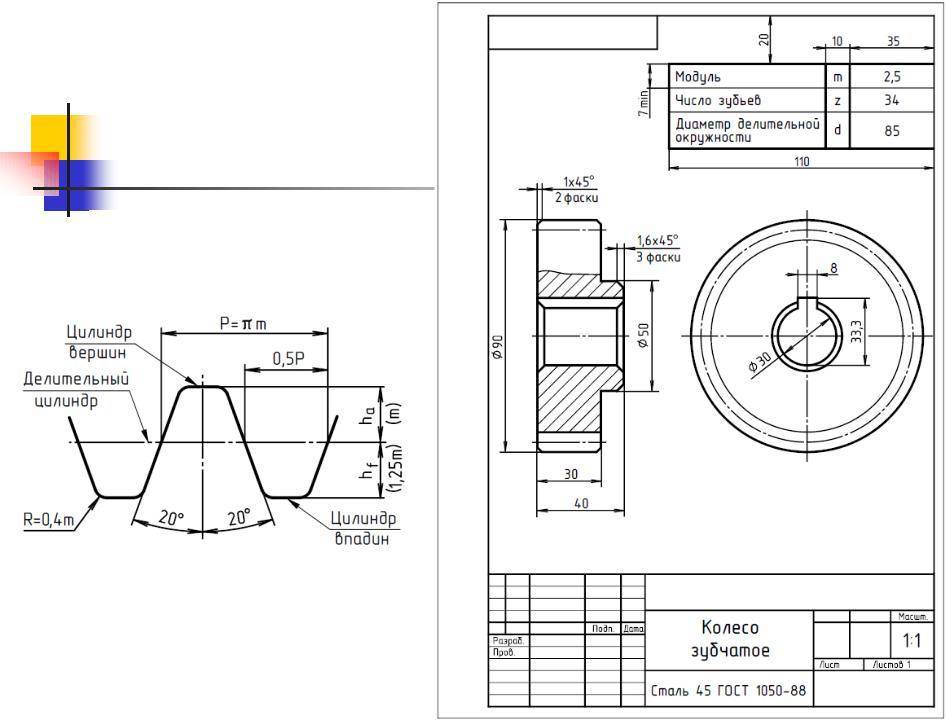
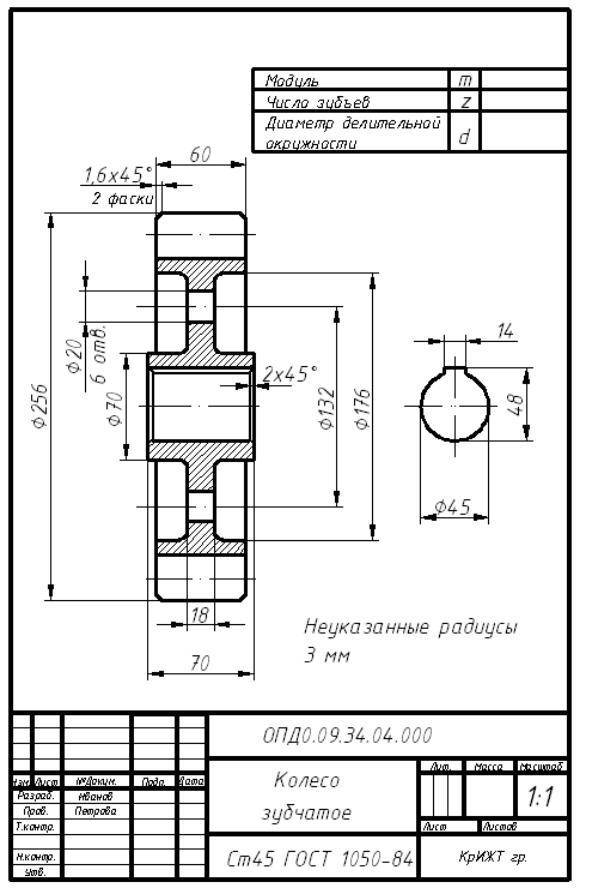
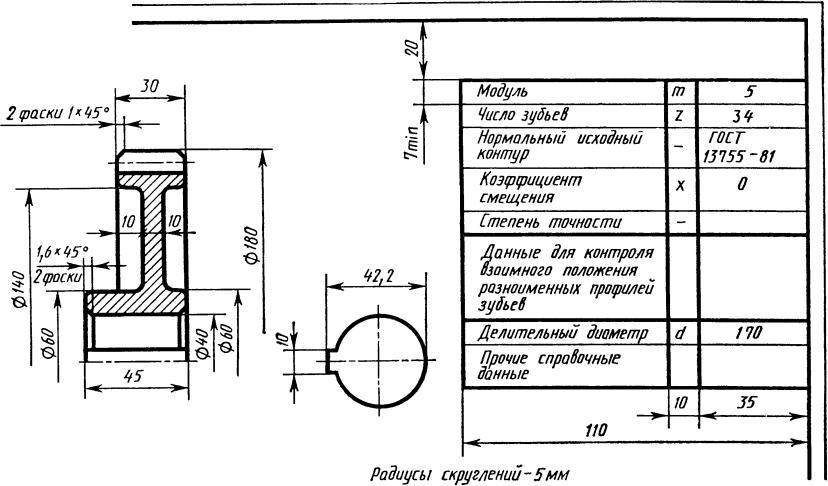
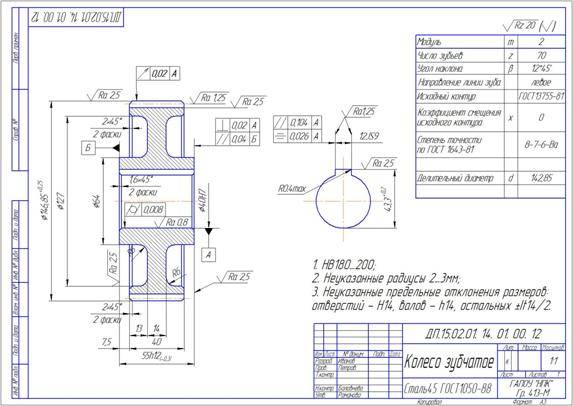
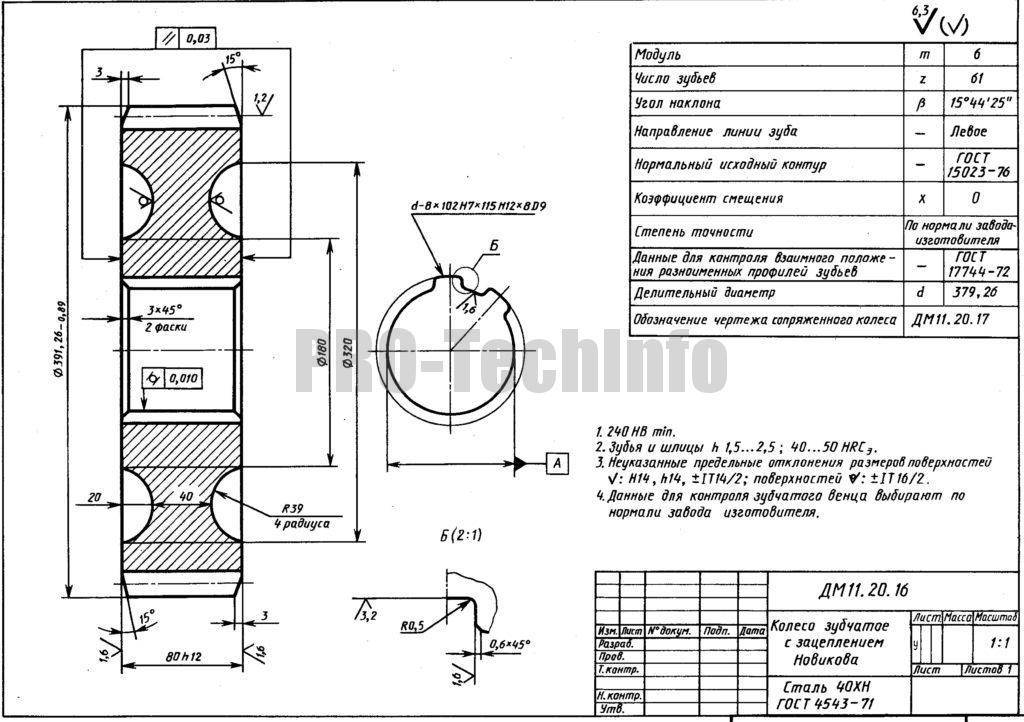
Зубчатое колесо — важнейшая составная часть многих конструкций приборов и механизмов, предназначенных для передачи или преобразования движения.Основные элементы зубчатого колеса: ступица, диск, зубчатый венец (рисунок 9.16).Рисунок 9.16 — Элементы зубчатого колесаПрофили зубьев нормализованы соответствующими стандартами.Основными параметрами зубчатого колеса являются (рисунок 9.17):m=P_t  / ? [мм] – модуль;d_a = m_ст (Z+2) – диаметр окружности вершин зубьев;d = m_ст Z – делительный диаметр;d_f  = m_ст (Z – 2.5) – диаметр окружности впадин;S_t = 0.5 m_ст ? – ширина зуба;h_a – высота головки зуба;h_f – высота ножки зуба;h = h_a+h_f – высота зуба;P_t  – делительный окружной шаг.Рисунок 9.17 — Параметры зубчатого колесаОсновная характеристика зубчатого венца — модуль — коэффициент, связывающий окружной шаг с числом ?. Модуль стандартизован (ГОСТ 9563-80).m = P_t / ?  

На учебных чертежах зубчатых колес:Высота головки зуба – h_a = m;Высота ножки зуба – h_f = 1,25m;Шероховатость рабочих поверхностей зуба – Ra 0.8 ;Справа вверху листа выполняют таблицу параметров, размеры которой приведены на рисунке 9.18, часто заполняют только значение модуля, число зубьев и делительный диаметр.Рисунок 9.18 — Таблица параметровЗубья колеса изображают условно, согласно ГОСТ 2.402-68 (Рисунок 9.19). Штрихпунктирная линия — делительная окружность колеса.В разрезе зуб показывают нерассеченным.

а	б	в

 Рисунок 9.19 — Изображение зубчатого колеса а — в разрезе, б — на виде спереди и в — на виде слеваШероховатость на боковую рабочую поверхность зуба на чертеже проставляют на делительной окружности.Пример выполнения чертежа зубчатого колеса приведен на рисунке 9.20.Рисунок 9.20 — Пример выполнения учебного чертежа зубчатого колеса

Что представляет собой шестерня

Шестерня – это небольшое колесико с зубьями, которое крепится к специальной вращающейся оси. Поверхность у шестеренки в данном случае может быть как конической, так и цилиндрической.

Шестеренчатые передачи также имеют свою классификацию:

1. Прямозубые. Наиболее распространенный вид шестеренок, у которых зубья зачастую располагаются в радиальных плоскостях.
2. Скошенные. По-другому этот тип называется еще косозубым, а его использование в ходу у бензо- и электрических инструментов. По отношению к вращающейся оси они находятся под определенным углом.
3. Червячные. Их еще называют спиральными шестернями, которые используются преимущественно для рулевого управления автомобилем.
4. Винтовые. Они имеют зачастую форму цилиндра, а также расположены по всей линии винта. Располагаются такие шестеренки на валах, которые расположены перпендикулярно к вращающейся оси.

Данные разновидности являются наиболее распространенными, однако далеко не единственными, поэтому используемый вид напрямую соотносится с тем, какую функцию он должен будет выполнять.

При этом каждая шестеренка имеет определенное количество зубьев, что определяется ее назначением. Разница между количеством используемых зубьев необходима, поскольку благодаря этому фактору появляется возможность регулировать обороты вала и крутящийся момент. Шестеренки также разделяются на ведущие и ведомые. Ведущей называется та шестерня, к которой вращательный момент подводится снаружи, а ведомой – та, с которой она снимается.

Почему шестеренку называют так?

Технически это понятно. Изначально «шестерёнка» — самое маленькое колесо в зубчатой передаче. Меньше шести зубьев там не бывает даже в теории, захват не обепечивается. … В машиностроении ведомое колесо зубчатой передачи редуктора называется колесом».

ОБЩИЕ ПОЛОЖЕНИЯ

1. ОБЩИЕ ПОЛОЖЕНИЯ

1.1. Принципиальная схема расчета геометрии приведена на чертеже.

1.2. Термины и обозначения, примененные в настоящем стандарте, соответствуют ГОСТ 16530-70* и ГОСТ 16531-70**. __________________ * Действует ГОСТ 16530-83; ** Действует ГОСТ 16531-83. – Примечание «КОДЕКС».

1.3. Наименования параметров, приводимых на рабочих чертежах зубчатых колес в соответствии с ГОСТ 2.403-75, а также межосевое расстояние зубчатой передачи, выделены в таблицах настоящего стандарта полужирным шрифтом.

1.4. При отсутствии в обозначениях параметров индексов «1» и «2», относящихся соответственно к шестерне и колесу, имеется в виду любое зубчатое колесо передачи.

1.5. При отсутствии дополнительных указаний везде, где упоминается профиль зуба, имеется в виду главный торцовый профиль зуба, являющийся эвольвентой основной окружности диаметра .

1.6. Расчетом определяются номинальные размеры зубчатой передачи и зубчатых колес.

1.7. Расчет некоторых геометрических и кинематических параметров, применяемых в расчете зубчатой передачи на прочность, приведен в приложении 5.

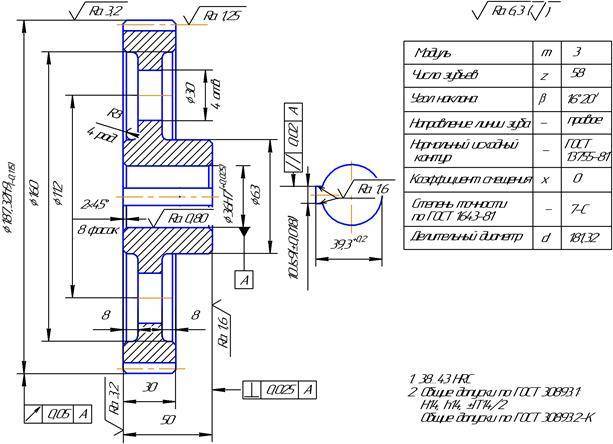
Чертеж шестерни

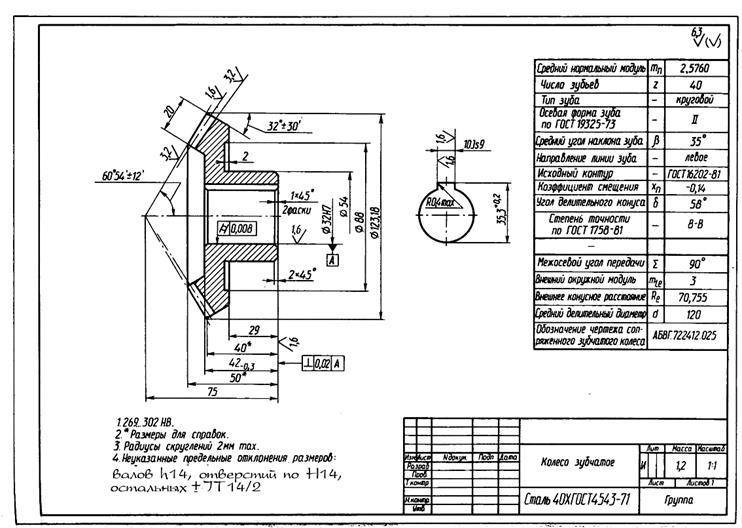
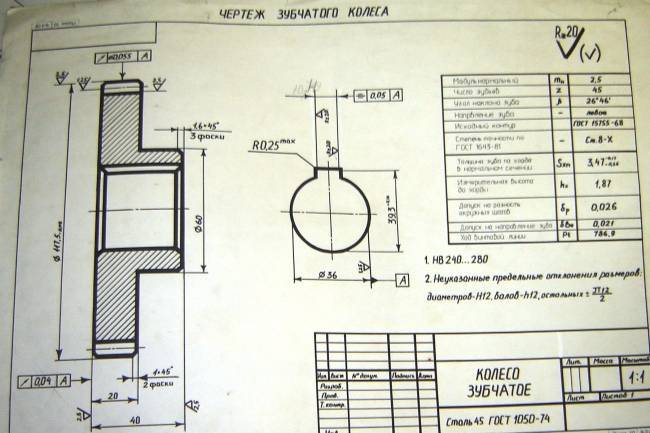
Чертеж шестерни должен выполняться в соответствии с требованиями ЕСКД, содержать главный вид и всю необходимую информацию:

• диаметр вершин зубьев (внешний) до притупления кромки
• диаметр вершин зубьев (внешний) после притупления кромки
• расстояние от базовой до внешней плоскости окружности верхней кромки зубьев
• угол конусности зубьев
• угол дополнительного конуса
• ширина венца
• расстояние базовое
• радиусы кривизны и размеры фасок
• положение сечения

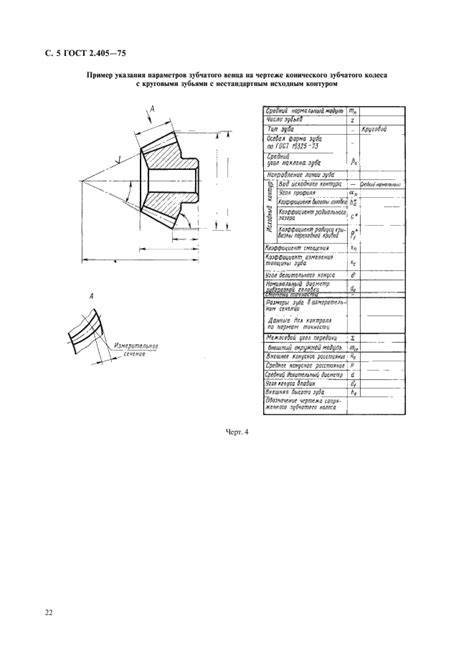
В правом углу чертежа, размещают таблицу, состоящую из трех частей, в которой указывают основные параметры:

• основные данные – верхняя часть
• контрольные данные – центральная часть
• справочные данные – нижняя часть

Справка:Неиспользуемые строки в таблице исключаются или ставится прочерк.Подробнее о каждой величине прописано в ГОСТ 2.405-75.

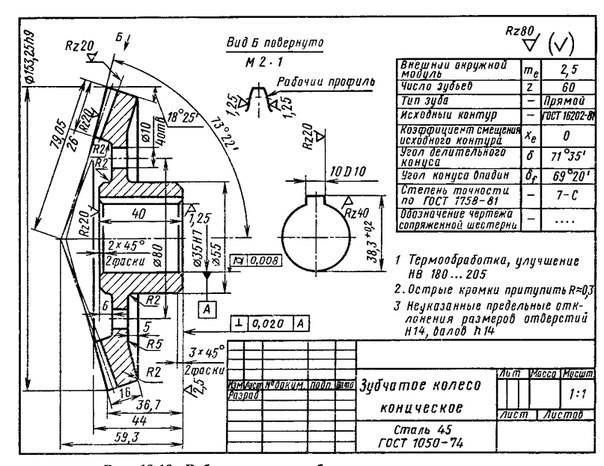
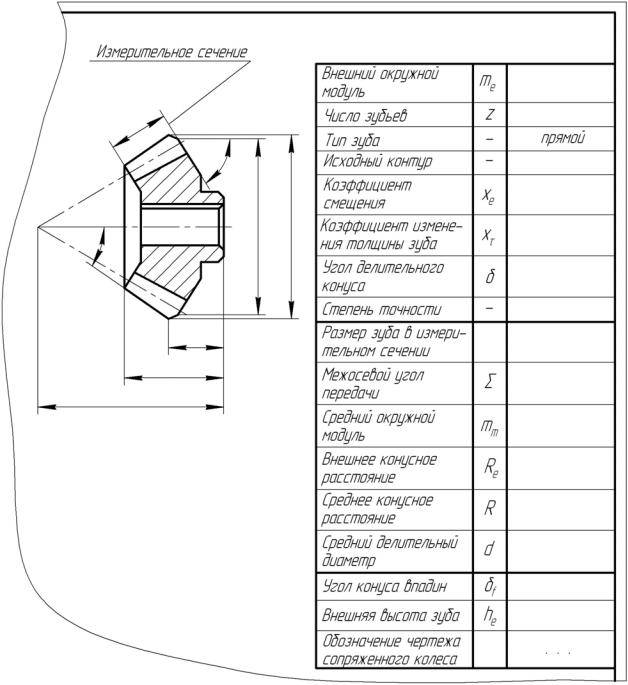
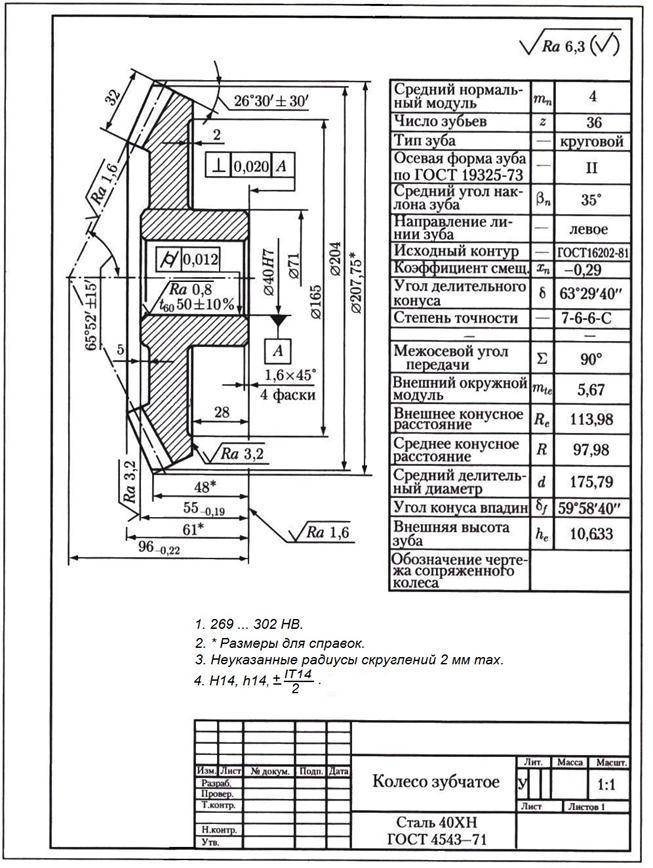
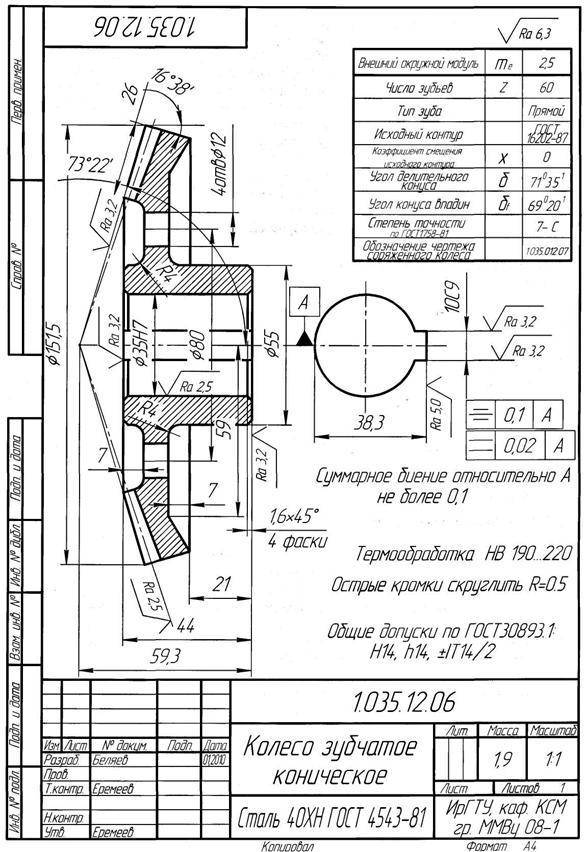
Чертеж конического колеса.

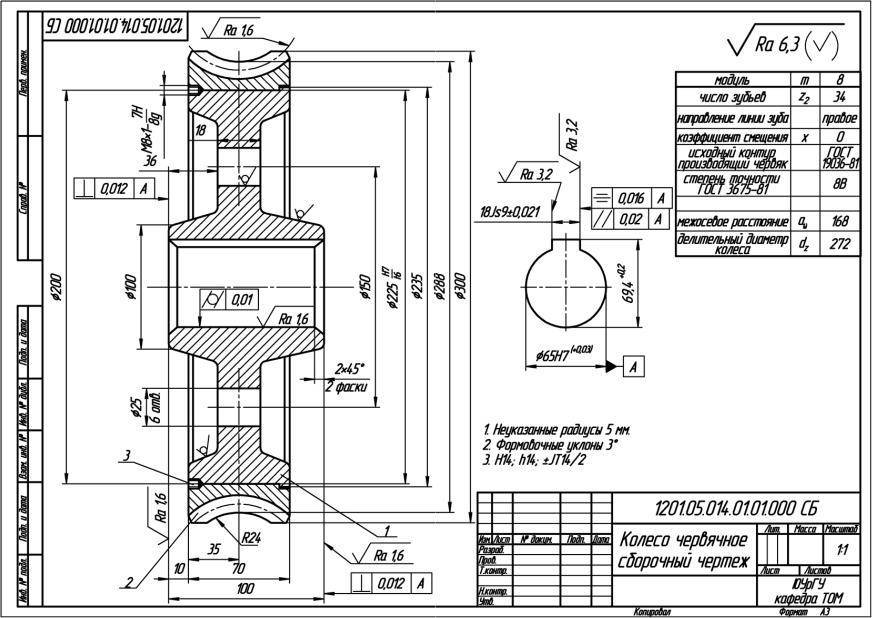
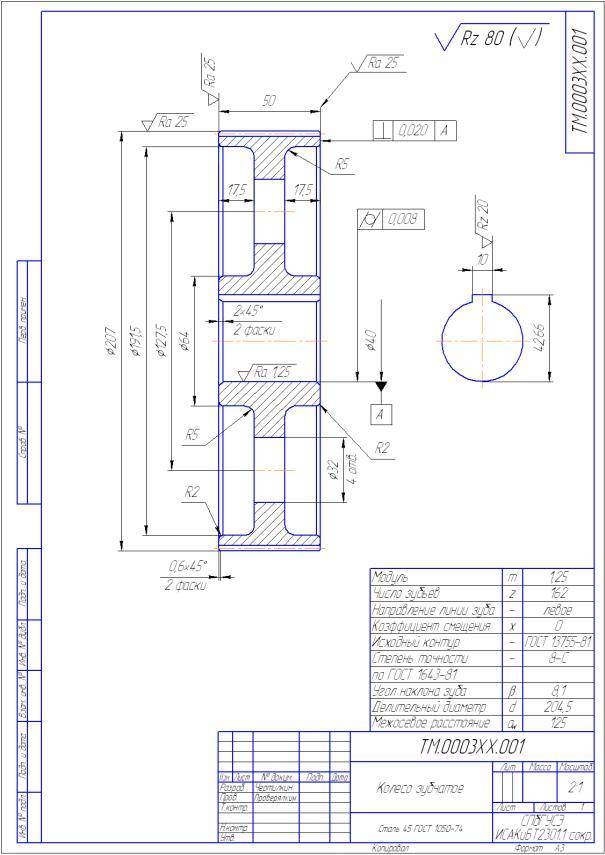
Чертеж червячного колеса.

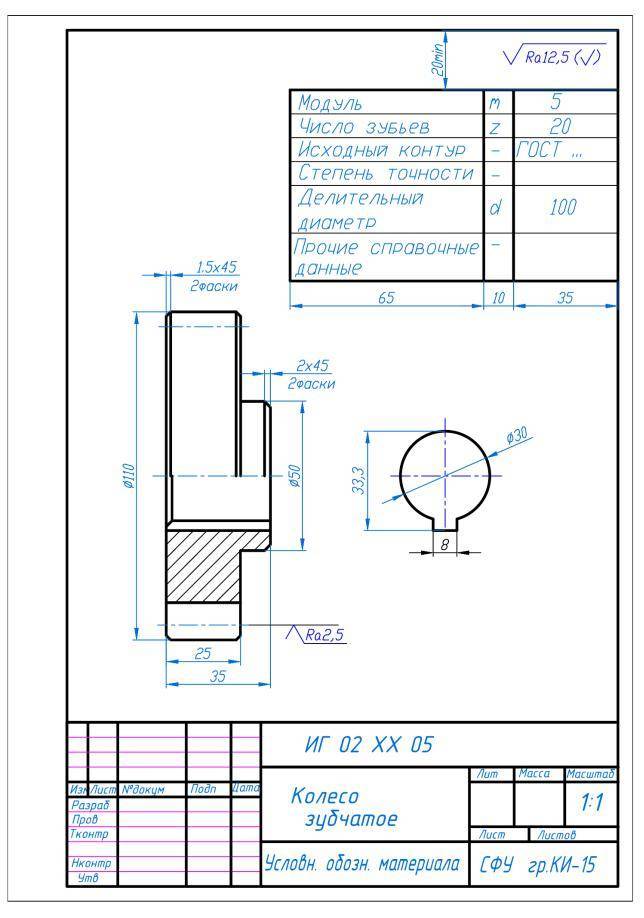
Шестерня.

Чертеж шестерни.

Конструктивное отличие зубчатых колес определяется:

• по геометрии зуба в поперечном сечении (форма) и способов контакта между собой: прямой – контактирует по точке; вогнутый – контактирует по линии; роликовый – контактирует с гребневым роликом.
• по типам колес: полное – когда оно постоянно вращается; сектор – когда оно поворачивается на определенный угол; сектор с роликом – когда рабочая длина контактируемого ролика уменьшена, по сравнению с контактируемой поверхностью глобоидального червяка.

Заказать чертеж

Документы

Сортировать по :
названию | дате | популярности

Шестерня m=2.5, Z=35

популярный!

Дата добавления:	08.06.2010
Дата изменения:	22.06.2010
Размер файла:	55.37 Кбайт
Скачиваний:	1305

Чертеж шестерни используемой в станке 2А554.

Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000

• Скачать

• Подробнее

Блок-шестерня m=2.5, Z1=33, Z2=19

популярный!

Дата добавления:	09.06.2010
Дата изменения:	22.06.2010
Размер файла:	51.48 Кбайт
Скачиваний:	1132

Чертеж блок-шестерни. Применяется в станке 2Л53У.

Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000

• Скачать

• Подробнее

Шестерня m=2.5, Z=20

популярный!

Дата добавления:	09.06.2010
Дата изменения:	22.06.2010
Размер файла:	41.4 Кбайт
Скачиваний:	1091

Чертеж шестерни с посадкой на шпонку. Используется в станке 2Л53У.

Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000

• Скачать

• Подробнее

Шестерня m=2.5, Z=51

популярный!

Дата добавления:	09.06.2010
Дата изменения:	22.06.2010
Размер файла:	50.61 Кбайт
Скачиваний:	1063

Чертеж шестерни с посадкой на шлицы. Применяется в станке 2Л53У.

Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000

• Скачать

• Подробнее

Вал-шестерня m=3, Z=21

Дата добавления:	09.06.2010
Дата изменения:	22.06.2010
Размер файла:	49.69 Кбайт
Скачиваний:	941

Чертеж вал-шестерни. Используется в станке 2Н57.

Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000

• Скачать

• Подробнее

Шестерня m=2.5, Z=30

Дата добавления:	09.06.2010
Дата изменения:	22.06.2010
Размер файла:	43.64 Кбайт
Скачиваний:	940

Чертеж шестерни. Используется в станке 2Н57.

Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000

• Скачать

• Подробнее

Шестерня m=2.5, Z=44

Дата добавления:	09.06.2010
Дата изменения:	22.06.2010
Размер файла:	43.79 Кбайт
Скачиваний:	946

Чертеж шестерни. Используется в станке 2Н57.

Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000

• Скачать

• Подробнее

Шестерня m=3, Z=24

популярный!

Дата добавления:	09.06.2010
Дата изменения:	22.06.2010
Размер файла:	43.27 Кбайт
Скачиваний:	1018

Чертеж шестерни. Используется в станке 2Н57.

Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000

• Скачать

• Подробнее

Шестерня m=2.5, Z=56

Дата добавления:	09.06.2010
Дата изменения:	22.06.2010
Размер файла:	43.82 Кбайт
Скачиваний:	995

Чертеж шестерни. Используется в станке 2Н57.

Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000

• Скачать

• Подробнее

Шестерня m=2.5, Z=39

Дата добавления:	09.06.2010
Дата изменения:	22.06.2010
Размер файла:	41.27 Кбайт
Скачиваний:	920

Чертеж шестерни. Используется в станке 2Н57.

Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000

• Скачать

• Подробнее

Исходные данные и замеры

На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.

Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.

Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.

Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.

Результаты расчетов

Для более крупных потребуются измерения и вычисления.

Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:

m=De/(z+2)

Последовательность действий следующая:

• измерить диаметр штангенциркулем;
• сосчитать зубцы;
• разделить диаметр на z+2;
• округлить результат до ближайшего целого числа.

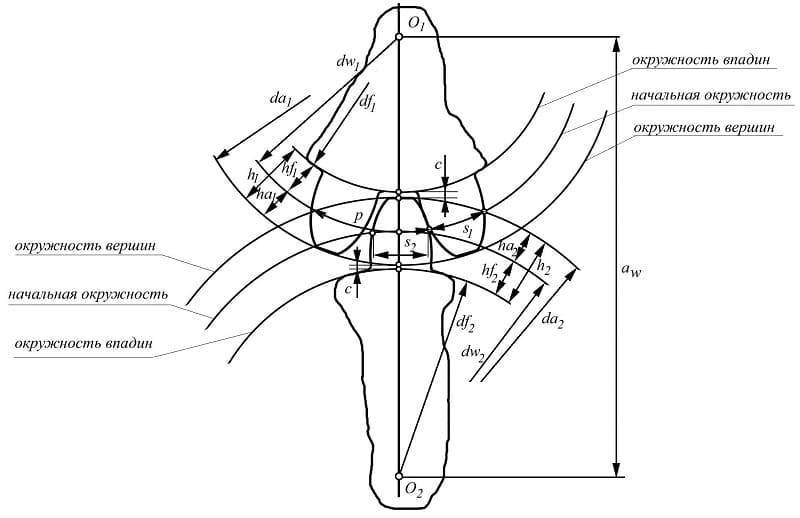
Зубец колеса и его параметры

Данный метод подходит как для прямозубых колес, так и для косозубых.

9.8. Выполнение чертежа пружины

Пружины применяются для создания определённых усилий в заданном направлении. По виду нагружения пружины подразделяются на пружины сжатия, растяжений, кручения и изгиба; по форме – на винтовые цилиндрические и конические, спиральные, листовые, тарельчатые и пр. правила выполнения чертежей различных пружин устанавливает ГОСТ 2.401-68. На чертежах пружины вычерчивают условно. Витки винтовой цилиндрической или конической пружины изображают прямыми линиями, касательными к участкам контура. Допускается в разрезе изображать только сечения витков. Пружины изображают с правой навивкой с указанием в технических требованиях истинного направления витков. Пример выполнения учебного чертежа пружины приведён на Рисунке 9.13.Чтобы получить на пружине плоские опорные поверхности крайние витки пружины поджимают на ? витка или на целый виток и шлифуют. Поджатые витки не считаются рабочими, поэтому полное число витков n равно числу рабочих витков плюс 1,5?2:n₁=n+(1.5?2) (Рисунок 9.14).Построение начинают с проведения осевых линия, проходящих через центры сечений витков пружины (Рисунок 9.15, а). Затем на левой стороне осевой линии проводят окружность, диаметр которой равен диаметру проволоки, из которой изготовлена пружины. Окружность касается  горизонтальной прямой, на которую опирается пружина. Затем необходимо провести полуокружность из центра, расположенного в пересечении правой оси с той же горизонтальной прямой. Для построения каждого последующего витка пружины слева на расстоянии шага строят сечения витков. Справа каждое сечение витка будет располагаться напротив середины расстояния между витками, построенными слева. Проводя касательные к окружностям, получают изображение пружины в разрезе, т.е. изображение витков, лежащих за плоскостью, проходящей через ось пружины. Для изображения передних половин витков так же проводят касательные к окружностям, но с подъёмом вправо (Рисунок 9.15, б). Переднюю четверть опорного витка строят так, чтобы касательная к полуокружности касалась одновременно и левой окружности в нижней части. Если диаметр проволоки 2мм и менее, то пружину изображают линиями толщиной 0,5?1,4мм. При вычерчивании винтовых пружин с числом витков более четырёх показывают с каждого конца один-два витка, кроме опорных проводя осевые линии через центры сечений витков по всей длине. На рабочих чертежах винтовые пружины изображают так, чтобы ось имела горизонтальное положение.Как правило, не рабочем чертеже помещают диаграмму испытаний, показывающую зависимость деформаций (растяжения, сжатия) от нагрузки (Р₁; Р₂; Р₃), где Н₁ – высота пружины при предварительной деформации Р₁; Н₂ – то же, при рабочей деформации Р₂; Н₃ – высота пружины при максимальной деформации Р₃; Н – высота пружины в рабочем состоянии. Кроме того, под изображением пружины указывают:

• Номер стандарта на пружину;
• Направление навивки;
• n – число рабочих витков;
• Полное число витков n;
• Длину развёрнутой пружины L=3,2?D?n₁;
• Размеры для справок;
• Другие технические требования.

На учебных чертежах рекомендуется из перечисленных пунктов указать п.п. 2,3,4,6. Выполнение диаграммы испытаний также не предусмотрено при выполнении учебного чертежа.Рисунок 9.13 – Рабочий чертеж пружины

а	б

Рисунок 9.14. Изображения поджатых витков пружиныРисунок 9.15. Последовательность построения изображения пружины

Диаметры окружностей

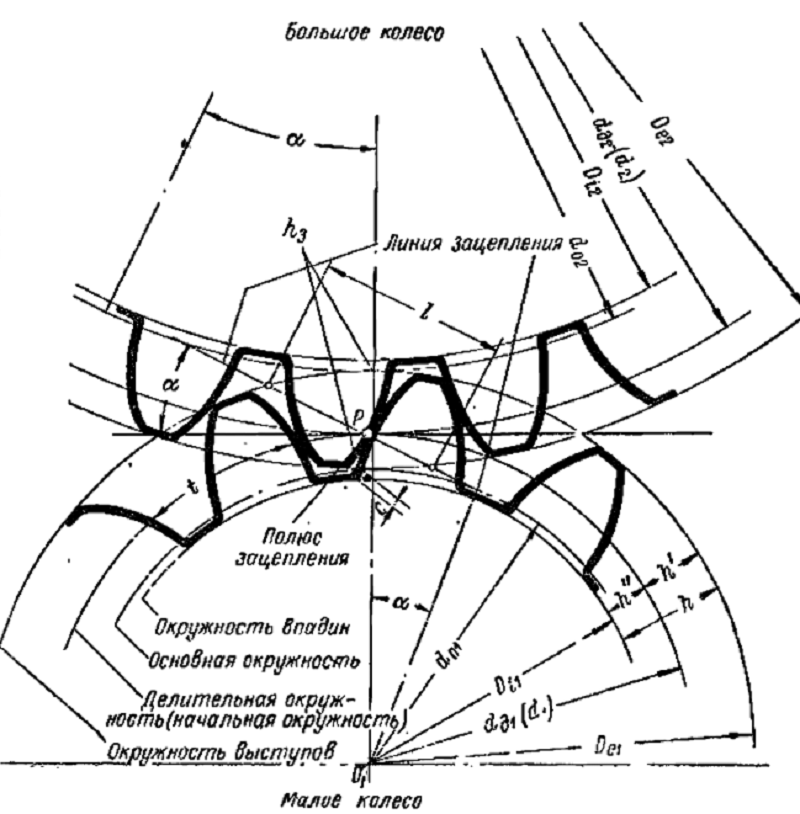
Рассмотрение геометрии зубчатых пар невозможно без определения диаметров. На каждой детали их выделяется несколько. Широкое распространение имеет диаметр окружности по выступам, иногда называемый диаметром вершин. Он определяет максимальные габариты диска колеса. Его противоположностью считается диаметр окружности впадин. Разность этих величин, поделенная пополам, дает полную длину зуба. Но этот параметр в чистом виде не используется. При расчетах принято выделять высоту головки и ножки зуба. Граница, отделяющая два этих понятия, называется делительной окружностью зубчатого колеса. Диаметр данной окружности выполняет функцию опорного параметра при выполнении расчетов геометрии, так как именно по ней определяется окружной шаг и модуль зацепления. Еще один диаметральный параметр, называемый основной окружностью, описывает теоретическую кривую, которая является базой при построении эвольвенты. Диаметр основной окружности используется для построения конкретного профиля зуба.

Классификация

Все многообразие колесных пар специалисты разделяют по различным признакам на несколько групп.

По взаиморасположению элементов

В данной категории выделяются такие виды зубчатых передач как:

• цилиндрическая (колеса в них находятся параллельно по отношению друг другу);
• коническая (с перекрещивающимися валами и, соответственно, деталями тандема);
• зубчато-винтовая (при скрещивающимся расположении элементов).

Первые используются наиболее широко, а их изготовление требует наименьших временных и финансовых затрат.

Детали конических передач по форме напоминают усеченный конус, и соприкасаются друг с другом боковыми сторонами. Это увеличивает площадь взаимодействующих поверхностей. Однако такая конструкция имеет большую чувствительность к погрешностям, и не способна выдерживать слишком большие нагрузки. Поэтому ее нередко используют в машинах и агрегатах, где есть другие типы зубчато-колесных механизмов.

Что касается зубчато-винтового типа, второе его название – червячный хорошо передает особенности соединения, которое состоит из червяка (винта) и колеса. К его достоинствам относят плавный ход, практическую бесшумность, большое передаточное отношение и способность к самоторможению.

По форме зуба

Зацепления в колесных связках отличаются по виду и профилю зубьев. На сегодняшний день известны:

• Зубчатые передачи эвольвентного зацепления. При таком варианте профили выступающих элементов колеса и шестерни очерчены по эвольвенте окружности. Это дает возможность сохранять стабильность передаваемой энергии при взаимодействии деталей.
• Циклоидальное. В нем профили зубьев очерчены по участкам циклоид. Достоинства этого вида – компактность в сочетании со способностью выдерживать усиленные нагрузки, плавность хода.
• Круговые (передача Новикова). Данный вид предполагает перемещение площадки контакта зубьев вдоль профиля зуба. Это обеспечивает более высокие значения передаточных чисел и возможность использовать даже при максимальных нагрузках.

Чаще всего, в механизмах применяются передачи с эвольвентным вариантом зацепления, что обусловлено достаточной простотой их изготовления, монтажа и эксплуатации. Циклоидальные и круговые передачи, в свою очередь, требуют больших затрат на производство, стоят дороже, но и позволяют обеспечить улучшенный функционал механизмов.

По расположению зубьев

По своему расположению зубья колеса и шестерни передачи бывают:

• Прямыми. Востребованы там, где необходимо передать крутящий момент с не очень большой и средней нагрузкой. Устанавливаются в механизмах с необходимостью смещения колес вдоль оси вала во время рабочего процесса.
• Косыми. Этот вариант позволяет повысить плавность вращения колес в тандеме.
• Шевронными – в виде «в елочку», сформированной из двух рядов косых зубьев.

Изготовление первого варианта деталей требует меньших финансовых и временных затрат, что снижает их стоимость и делает наиболее востребованными. Однако второй и третий вариант обладают рядом неоспоримых достоинств, которые позволяют комплектовать ими наиболее ответственные механизмы, работающие в условиях повышенных нагрузок.

Другие варианты классификации

Помимо особенностей взаиморасположения элементов в колесной паре, форм и расположения зубьев на них, передачи также классифицируются по:

• Конструкции (открытые и закрытые). Вторые могут работать только при постоянном наличии смазки, первые функционируют на сухом ходу.
• Окружной скорости (тихоходные – до 3 м/с; средние – от 3 до 15 м/с; быстроходные – свыше 15 м/с).
• Числу ступеней (одно- и многоступенчатые).
• Точности зацепления (существует 12 степеней, однако чаще всего используют с 6 по 10).

Кроме того, различают силовые зубчатые передачи и кинематические (не силовые). Первые передают вращающий момент и их размеры зависят от прочности зубьев. Вторые же практически не передают нагрузку, а их габариты определяются конструктивными особенностями.

Неметаллические зубчатые колеса.

Неметаллические зубчатые колеса. Зубчатые колеса из пластмасс (текстолит, древопластики, полиамиды и т. п.) работают более бесшумно, чем металлические, что имеет особое значение при больших скоростях. Чтобы понизить коэффициент трения между зубьями, одно зубчатое колесо делают из пластмассы, а второе выполняют металлическим. Пластмассы имеют сравнительно небольшие сопротивления срезу и смятию, поэтому в большинстве случаев для передачи момента применяют стальную втулку-ступицу, прочно соединяемую с телом колеса. В небольшие колеса ступицу устанавливают при формовании. Для лучшего сцепления наружную поверхность ступицы делают рифленой (накатанной) (рис. 12). Чтобы предотвратить выкрашивание и откалывание отдельных слоев пластмассы, края зубьев защищают стальными дисками (рис. 13). Толщину диска рекомендуется принимать равной половине модуля, но не более 8 мм и не менее 2 мм. Материал дисков —сталь Ст.2, Ст.З.

Зубчатые колеса больших размеров обычно делают сборными из отдельных секций.

Ширину зубчатого колеса из пластмасс принимают равной ширине зацепляющегося с ним металлического колеса или несколько меньше во избежание местного износа и выработки зубьев