Модуль зубьев зубчатого колеса

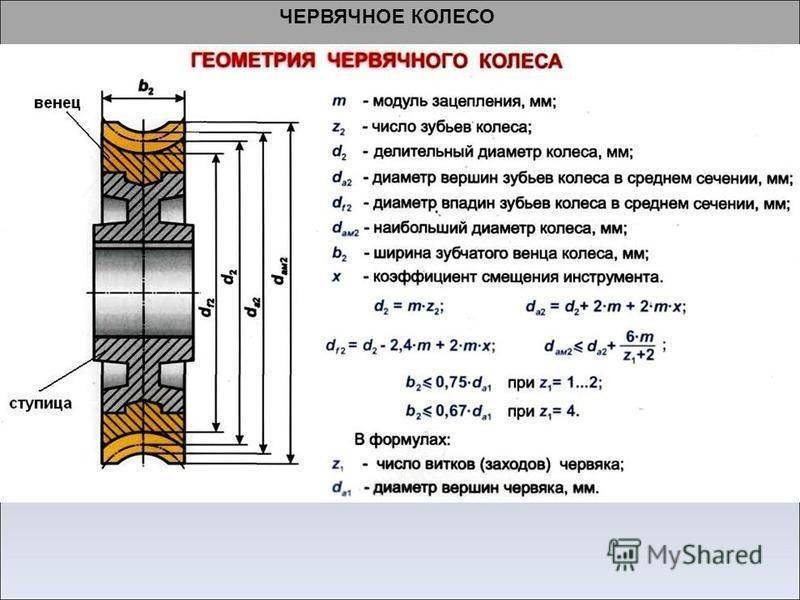
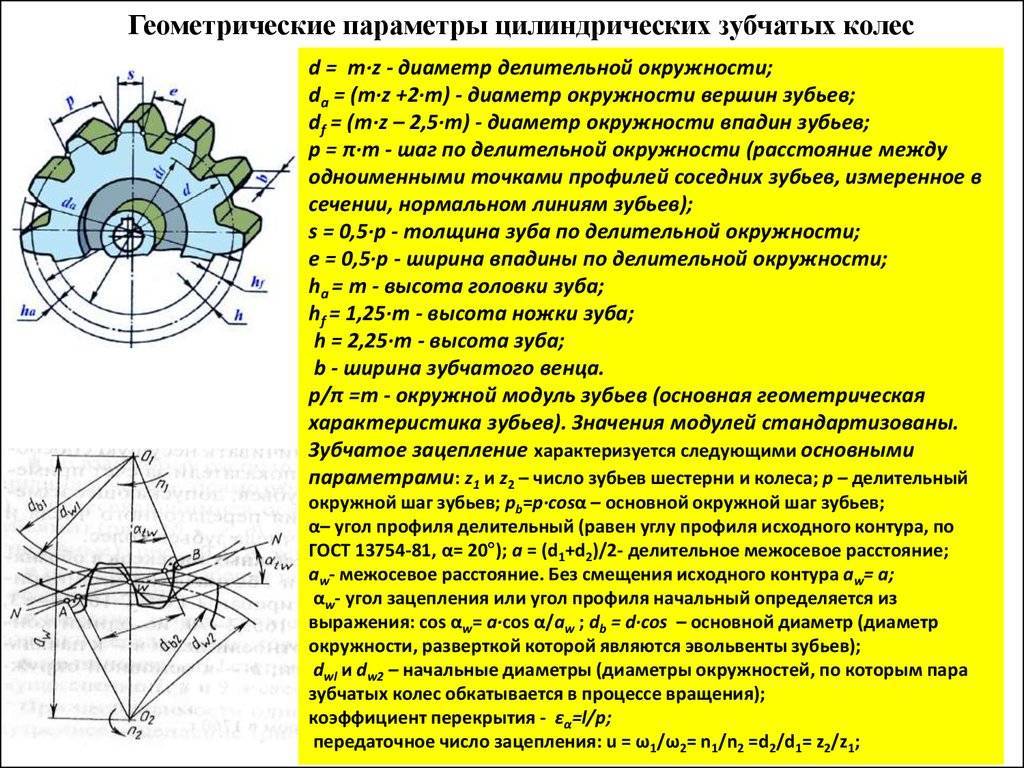
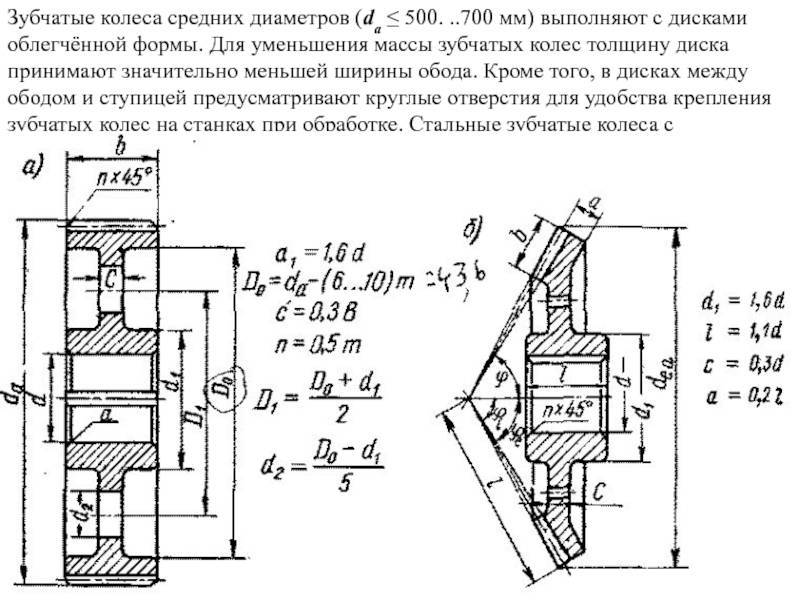
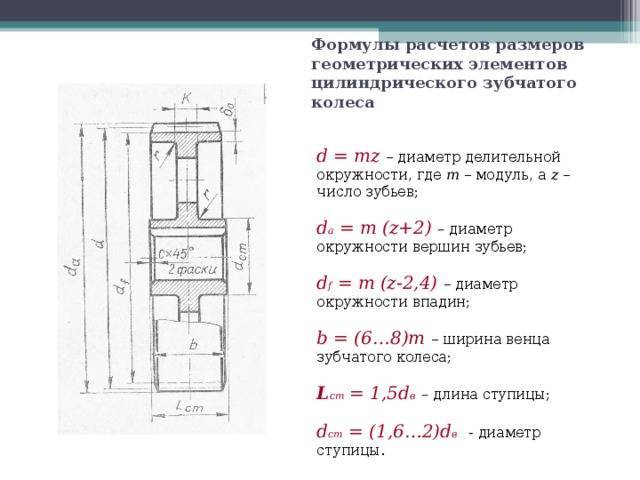
Основные ошибки самостоятельной замены

Несмотря на предельно простую технологию, автолюбители часто допускают при замене венца следующие ошибки:

• перед тем, как снять зубчатый обод, следует произвести ревизию боковой плоскости маховика под сцепление, и отверстий для крепежных болтов;
• установка с перегревом отдельных участков венца приведет к быстрому износу зубьев именно на этих местах, так как происходит отпуск стали;
• наружный диаметр зубьев должен иметь фаску для плавного зацепления с бендиксом стартера без ударов.

Для того, чтобы уменьшить износ двигателя и увеличить приемистость машины на высоких оборотах, маховик часто облегчают. Из-за наличия дополнительных отверстий на наружном диаметре диска в зоне, примыкающей к зубчатому ободу, венец часто приваривается к диску.

Таким образом, венец можно заменить собственными силами при значительной выработке профиля зуба на отдельных участках. Снять обод можно на холодную, а при установке потребуется нагрев до 200 градусов максимум.

Стандарты зубчатых передач США

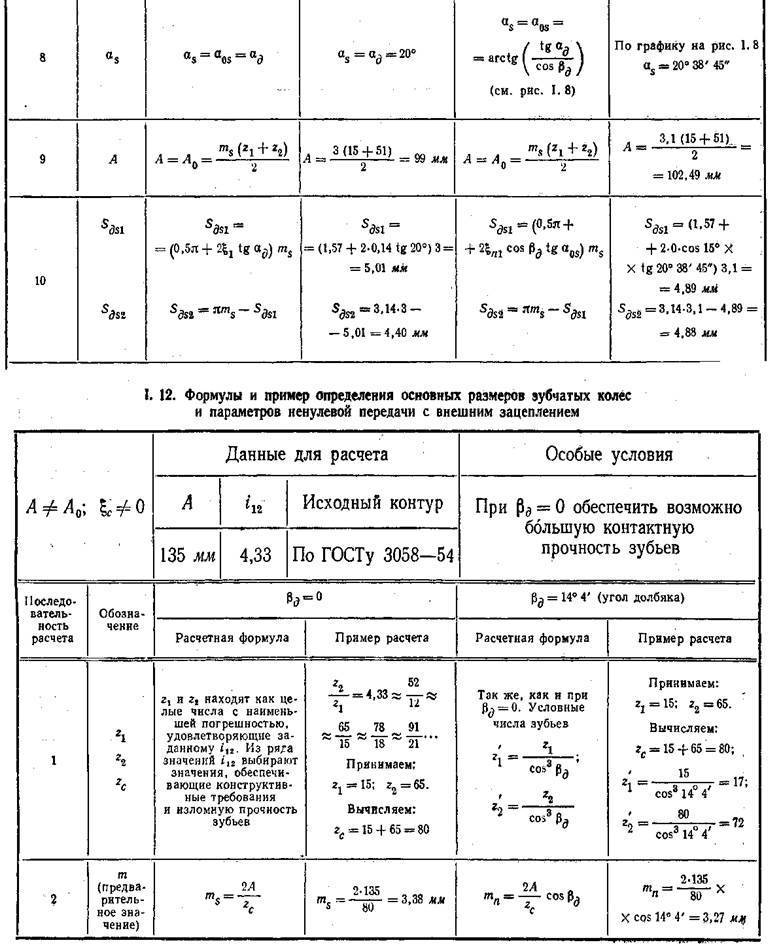
Вместо модуля для стандартизации зубча­тых передач в США используется показатель количества зубьев на 1 дюйм (25,4 мм) диа­метра делительной окружности или диамет­ральный модуль (питч) (Р):

Р = z/d = z/(z • m/25,4) =25,4/m

Для перевода стандарта США в европейский стандарт служит зависимость:

m = 25,4 мм / P

Размещение зубьев в пределах диаметраль­ного модуля называется окружным шагом зацепления (CP):

CP = (25,4 мм / P) π.

Табл. Стандарты зубчатых передач

Полная высота зуба

В стандартах США полная высота зуба обо­значается как высота головки h_a = т, что соответствует величине т в стандартах Гер­мании.

Ножка зуба

Обозначается так же, как и полная вы­сота зуба, но расчет головки зуба основы­вается на использовании своего модуля. Пример обозначения:

Обозначение (пример): Р 5 /7

Р = 7 для расчета головки зуба,

Р = 5 для расчета других параметров.

Система обозначений и преобразований

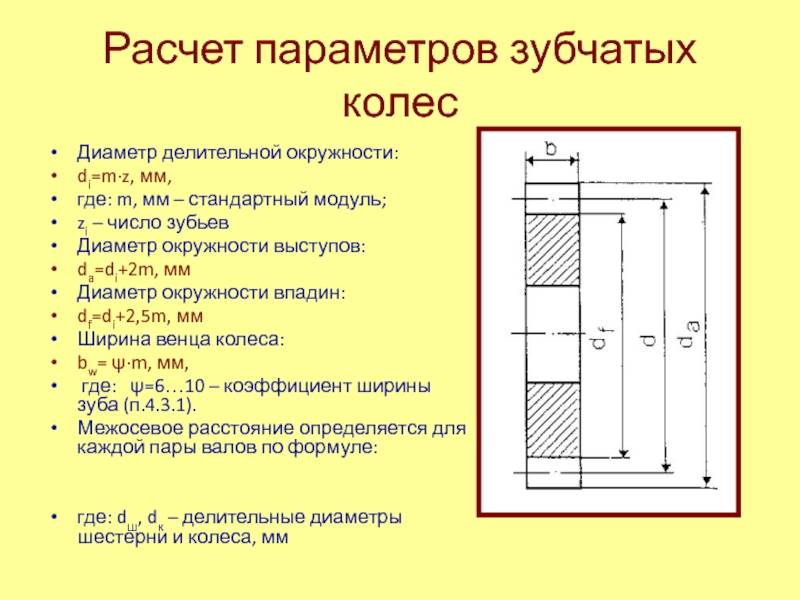
Диаметр окружности выступов: OD = d_a.

Диаметр делительной окружности: PD = N/P = d (в дюймах) или PD = Nm = d (в мм).

Диаметр окружности впадин: RD = d_f

LD =(N+2x) / P (в дюймах)

LD= (N+2x)·m (в мм).

где d_w — диаметральный модуль.

Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

π×D=t× z,

проведя преобразование, получим:

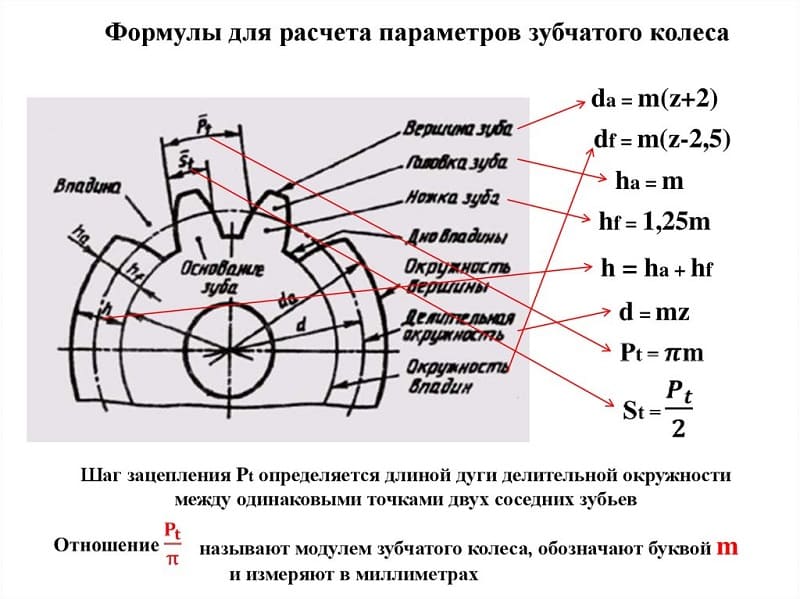
Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

выполнив преобразование, находим:

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов D e получается равным

где h’- высота головки.

Высоту головки приравнивают к m:

Проведя математические преобразования с подстановкой, получим:

De=m×z+2m = m(z+2),

откуда вытекает:

Диаметр окружности впадин D i соответствует D e за вычетом двух высот основания зубца:

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

Выполнив подстановку в правой части равенства, имеем:

D i = m×z-2×1,25m = m×z-2,5m;

что соответствует формуле:

D i = m(z-2,5m).

Полная высота:

и если выполнить подстановку, то получим:

h = 1m+1,25m=2,25m.

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины s в, получаем формулы для ширины впадины

• для отлитых зубцов: s в =πm-1,53m=1,61m:
• для выполненных путем фрезерования- s в = πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

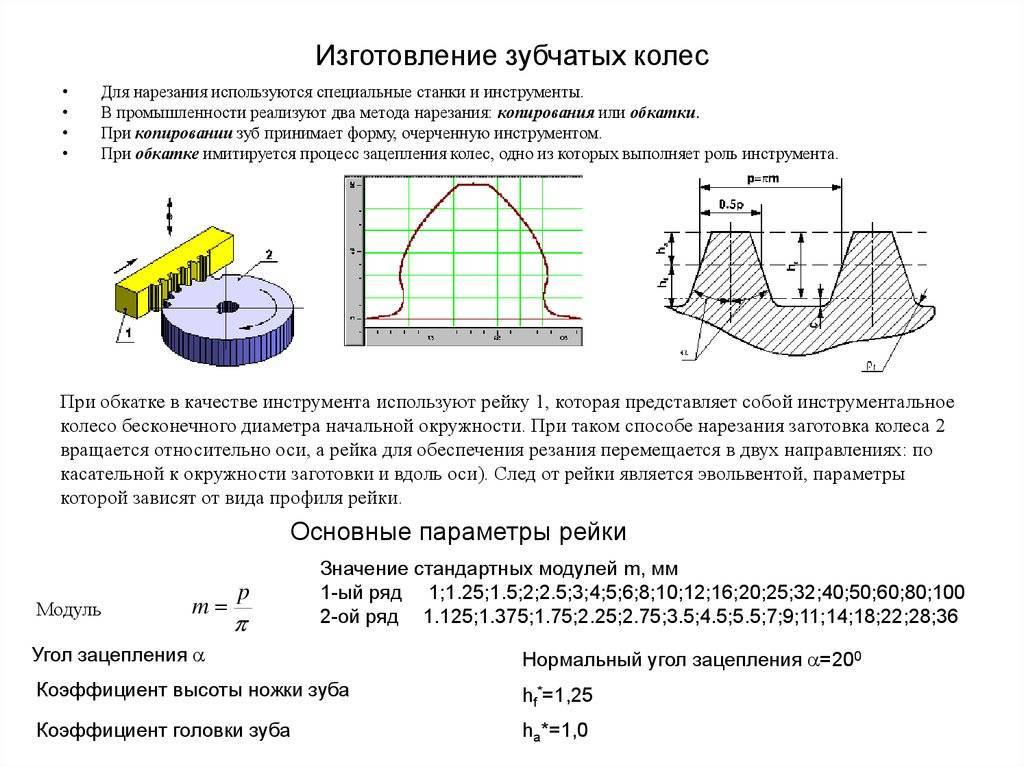
Зубчатая рейка

Зубчатая рейка является частью зубчатого колеса с бесконечным радиусом делительной окружности. Вследствие этого ее окружности представляют собой прямые параллельные линии. Эвольвентный профиль зубчатой рейки тоже имеет прямолинейное очертание. Это свойство эвольвенты является наиболее важным при изготовлении зубчатых колёс. Передачу с применением зубчатой планки (рейки) называют – реечная передача (кремальера), она используется для преобразования вращательного движения в поступательное и наоборот. Состоит передача из зубчатой рейки и прямозубого зубчатого колеса (шестеренки). Применяется такая передача в зубчатой железной дороге.

Расчет наибольшего допустимого давления зубчатых передач

Ниже приведены расчетные формулы, кото­рые могут применяться вместо стандартного расчета DIN 3990 «Расчет несущей способ­ности зубчатых передач». Эти зависимости применимы для расчета нагрузки транс­миссионных зубчатых пар, работающих в стандартном режиме.

Величины и единицы измерения для расчета наибольшего допустимого давления

Необходимое сопротивление усталост­ному выкрашиванию и изнашиванию металла для шестерни (колесо 1) вследствие высо­кого контактного давления достигается, если величина оценки сопротивления выкрашива­нию S_w равна или больше 1. В случае зубча­того зацепления с z₁< 20 следует принимать S_w ⩾ 1,2…1,5 из-за более высоких контактных напряжений в точке однопарного зацепления. Поскольку контактные давления равны по ве­личине для обоих колес, значение k_perm для зубчатого колеса 2 следует принимать такими же, как и для колеса 1 при частоте вращения n₂, пользуясь помещаемой ниже таблицей.

Формулы для расчета наибольшего допустимого давления

Содержащиеся в таблице значения коэф­фициента &_Perm применимы, когда оба колеса изготовлены из стали. Для пар зубчатых ко­лес из чугуна и стали или бронзы и стали этот коэффициент следует увеличить в 1,5 раза. В случае зубчатых пар из чугуна по чугуну или бронзы по бронзе коэффициент k_perm следует увеличить примерно в 1,8 раза. Для зубча­того зацепления лишь с одним поверхностно упрочненным колесом, коэффициент k_perm для незакаленного колеса необходимо уве­личить на 20%. Все приведенные в таблице значения этого коэффициента рассчитаны на срок службы L_h = 5000 ч. При оценке сопро­тивления выкрашиванию металла зубчатых колес S_w расчетный срок их службы может изменяться за счет коэффициента срока службы ф.

Коэффициент допустимого контактного давления k_perm в H/mm2 для срока службы L_h = 5000 ч

Прочностные характеристики материалов для изготовления зубчатых передач приве­дены в табл. «Параметры материалов зубчатых передач«.

1. При пульсирующей нагрузке для предела усталостной прочности (N_L ⩾ 3_*106). В случае знакопеременной      нагрузки следует применять коэффициент Y_L
2. В пределах усталостной прочности в течение срока службы напряжения изгиба увеличиваются на коэффици­ент Y_nt в зависимости от количества циклов нагрузки N_L.

Коэффициент срока службы ф

Коэффициент срока службы используется для корректирования приведенных в верх­ней таблице значений коэффициента допу­стимого контактного давления k_perm (рас­считанного на срок службы L_h = 5000 ч) для различной расчетной продолжительности работы зубчатой передачи.

Рекомендации по выбору расчетного срока службы зубчатых передач: при посто­янной работе с полной нагрузкой — от 40 000 до 150 000 ч; при прерывистой полной на­грузке — от 50 до 5000 ч.

Необходимая величина сопротивления разрушению зуба обеспечивается при S_F ⩾ 1 для шестерни (колесо 1). Если шестерня изготовлена из более проч­ного материала, чем зубчатое колесо 2, сле­дует также произвести проверочный расчет зубчатого колеса на изгибающие нагрузки.

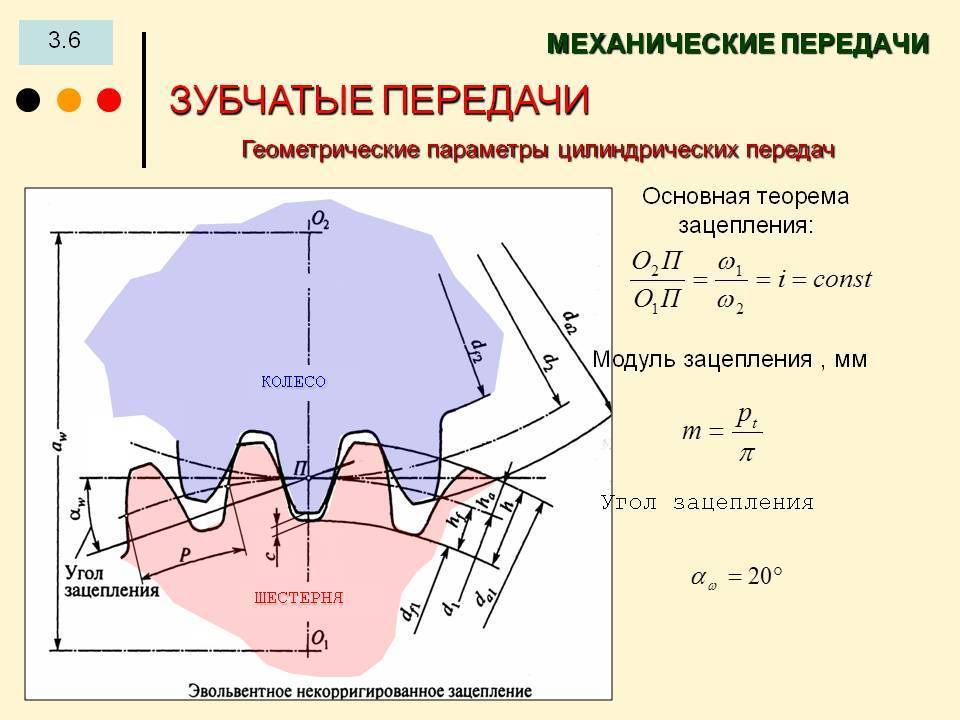
Эвольвентное зацепление

Эвольвентное зацепление — это зубчатая передача, которая нечувст­вительна к изменению межосевого расстоя­ния. Его изготавливают методом обкатки.

Все прямозубые цилиндрические передачи с одинаковым модулем зацепления могут из­готавливаться на одном оборудовании, не­зависимо от количества зубьев и размеров головки.

Модули зацепления цилиндрических и ко­нических зубчатых колес стандартизированы по DIN 780; модули зацепления червячных пе­редач по DIN 780; модули шлицевых соедине­ний по DIN 5480; модули зубчатого зацепле­ния нормального профиля для шестерен со спиральными зубьями по DIN 780.

Форма зубьев

Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; чер­вячных передач — DIN 3975; шлицевых соеди­нений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).

Форма зубьев гипоидных передач регла­ментируется стандартом DIN 867. В допол­нение к стандартным углам зацепления (20° для зубчатых передач и 30° для шлицевых соединений) применяются также и углы заце­пления 12°, 14°30\ 15°, 17°30′_| 22°30′ и 25°.

Рис. Характеристики прямозубой цилиндрической передачи передачи (циклоидное зацепление)

Коррегирование зубчатого зацепления

Коррегирование зубчатого зацепления (из­менение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подреза­ния у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.

Зубчатые передачи с точно заданным межосевым расстоянием

У зубчатых пар с точно заданным межосевым расстоянием изменение высоты головки зуба для шестерни и зубчатого колеса произво­дится на одинаковую величину, но в противо­положных направлениях, что позволяет сохранить межосевое расстояние неизменным. Такое решение применяется в гипоидных и косозубых передачах.

Зубчатые передачи с изменяемым межосевым расстоянием

Изменение высоты головки зуба для ше­стерни и зубчатого колеса производится независимо друг от друга, поэтому межосе­вое расстояние передачи может изменяться. Допускаемые отклонения линейных разме­ров зубчатых передач регламентированы. Для прямозубых цилиндрических передач — DIN 3960, DIN 58405; для конических передач — DIN 3971; червячных передач — DIN 3975.

Подставляя j_η = 0 в приведенные ниже формулы, рассчитывают параметры за­цепления без зазора между зубьями. Для определения зазора между зубьями допу­скаемые отклонения толщины зубьев и зоны их зацепления принимают в соответствии со стандартами DIN 3967 и DIN 58405 в за­висимости от требуемой степени точности зубчатой передачи. Следует отметить, что не обязательно стремиться к нулевому за­зору между зубьями. Для компенсации имею­щихся отклонений размеров зубьев и сборки шестерен достаточно иметь минимальный зазор, который, кроме того, предотвращает возможность заклинивания зубчатых колес. Допускаемые отклонения других расчетных параметров (зазор между ножками двух смежных зубьев, межцентровое расстояние) приведены в стандартах DIN 3963, DIN 58405, DIN 3962 Т2, DIN 3967, DIN 3964.

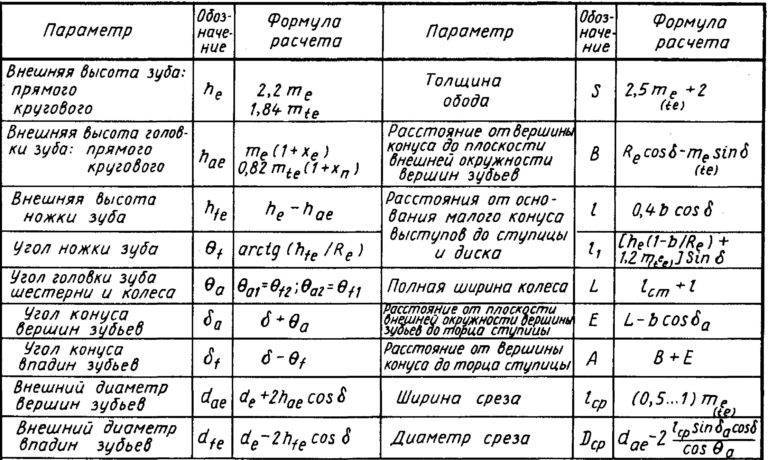
В таблице ниже приведены формулы для расчета зубчатой передачи:

Что представляет собой шестерня

Шестерня – это небольшое колесико с зубьями, которое крепится к специальной вращающейся оси. Поверхность у шестеренки в данном случае может быть как конической, так и цилиндрической.

Шестеренчатые передачи также имеют свою классификацию:

1. Прямозубые. Наиболее распространенный вид шестеренок, у которых зубья зачастую располагаются в радиальных плоскостях.
2. Скошенные. По-другому этот тип называется еще косозубым, а его использование в ходу у бензо- и электрических инструментов. По отношению к вращающейся оси они находятся под определенным углом.
3. Червячные. Их еще называют спиральными шестернями, которые используются преимущественно для рулевого управления автомобилем.
4. Винтовые. Они имеют зачастую форму цилиндра, а также расположены по всей линии винта. Располагаются такие шестеренки на валах, которые расположены перпендикулярно к вращающейся оси.

Данные разновидности являются наиболее распространенными, однако далеко не единственными, поэтому используемый вид напрямую соотносится с тем, какую функцию он должен будет выполнять.

При этом каждая шестеренка имеет определенное количество зубьев, что определяется ее назначением. Разница между количеством используемых зубьев необходима, поскольку благодаря этому фактору появляется возможность регулировать обороты вала и крутящийся момент. Шестеренки также разделяются на ведущие и ведомые. Ведущей называется та шестерня, к которой вращательный момент подводится снаружи, а ведомой – та, с которой она снимается.

Почему шестеренку называют так?

Технически это понятно. Изначально «шестерёнка» — самое маленькое колесо в зубчатой передаче. Меньше шести зубьев там не бывает даже в теории, захват не обепечивается. … В машиностроении ведомое колесо зубчатой передачи редуктора называется колесом».

Расчет наибольшего допустимого давления зубчатых передач

Ниже приведены расчетные формулы, кото­рые могут применяться вместо стандартного расчета DIN 3990 «Расчет несущей способ­ности зубчатых передач». Эти зависимости применимы для расчета нагрузки транс­миссионных зубчатых пар, работающих в стандартном режиме.

Величины и единицы измерения для расчета наибольшего допустимого давления

Необходимое сопротивление усталост­ному выкрашиванию и изнашиванию металла для шестерни (колесо 1) вследствие высо­кого контактного давления достигается, если величина оценки сопротивления выкрашива­нию S_w равна или больше 1. В случае зубча­того зацепления с z₁ 2 для срока службы L_h = 5000 ч

Прочностные характеристики материалов для изготовления зубчатых передач приве­дены в табл. «Параметры материалов зубчатых передач«.

1. При пульсирующей нагрузке для предела усталостной прочности (N_L ⩾ 3_*10 6 ). В случае знакопеременной нагрузки следует применять коэффициент Y_L
2. В пределах усталостной прочности в течение срока службы напряжения изгиба увеличиваются на коэффици­ент Y_nt в зависимости от количества циклов нагрузки N_L.

Коэффициент срока службы ф

Коэффициент срока службы используется для корректирования приведенных в верх­ней таблице значений коэффициента допу­стимого контактного давления k_perm (рас­считанного на срок службы L_h = 5000 ч) для различной расчетной продолжительности работы зубчатой передачи.

Рекомендации по выбору расчетного срока службы зубчатых передач: при посто­янной работе с полной нагрузкой — от 40 000 до 150 000 ч; при прерывистой полной на­грузке — от 50 до 5000 ч.

Необходимая величина сопротивления разрушению зуба обеспечивается при S_F ⩾ 1 для шестерни (колесо 1). Если шестерня изготовлена из более проч­ного материала, чем зубчатое колесо 2, сле­дует также произвести проверочный расчет зубчатого колеса на изгибающие нагрузки.

Зубчатые передачи

Зубчатые передачи — это механизм или часть механизма механической передачи, в состав которого входят зубчатые колёса. Зубчатые передачи служат для того, чтобы непрерывно передавать силу и крутящий момент двух валов, расположение которых определяет тип имеющейся зубчатой передачи. Вот о том, что представляют зубчатые передачи, мы и поговорим в этой статье.

Эвольвентное зацепление

Все прямозубые цилиндрические передачи с одинаковым модулем зацепления могут из­готавливаться на одном оборудовании, не­зависимо от количества зубьев и размеров головки.

Модули зацепления цилиндрических и ко­нических зубчатых колес стандартизированы по DIN 780; модули зацепления червячных пе­редач по DIN 780; модули шлицевых соедине­ний по DIN 5480; модули зубчатого зацепле­ния нормального профиля для шестерен со спиральными зубьями по DIN 780.

Форма зубьев

Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; чер­вячных передач — DIN 3975; шлицевых соеди­нений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).

Форма зубьев гипоидных передач регла­ментируется стандартом DIN 867. В допол­нение к стандартным углам зацепления (20° для зубчатых передач и 30° для шлицевых соединений) применяются также и углы заце­пления 12°, 14°30 15°, 17°30′| 22°30′ и 25°.

Коррегирование зубчатого зацепления

Коррегирование зубчатого зацепления (из­менение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подреза­ния у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.

Зубчатые передачи с точно заданным межосевым расстоянием

У зубчатых пар с точно заданным межосевым расстоянием изменение высоты головки зуба для шестерни и зубчатого колеса произво­дится на одинаковую величину, но в противо­положных направлениях, что позволяет сохранить межосевое расстояние неизменным. Такое решение применяется в гипоидных и косозубых передачах.

Зубчатые передачи с изменяемым межосевым расстоянием

Изменение высоты головки зуба для ше­стерни и зубчатого колеса производится независимо друг от друга, поэтому межосе­вое расстояние передачи может изменяться. Допускаемые отклонения линейных разме­ров зубчатых передач регламентированы. Для прямозубых цилиндрических передач — DIN 3960, DIN 58405; для конических передач — DIN 3971; червячных передач — DIN 3975.

Подставляя jη = 0 в приведенные ниже формулы, рассчитывают параметры за­цепления без зазора между зубьями. Для определения зазора между зубьями допу­скаемые отклонения толщины зубьев и зоны их зацепления принимают в соответствии со стандартами DIN 3967 и DIN 58405 в за­висимости от требуемой степени точности зубчатой передачи.

Следует отметить, что не обязательно стремиться к нулевому за­зору между зубьями. Для компенсации имею­щихся отклонений размеров зубьев и сборки шестерен достаточно иметь минимальный зазор, который, кроме того, предотвращает возможность заклинивания зубчатых колес.

Допускаемые отклонения других расчетных параметров (зазор между ножками двух смежных зубьев, межцентровое расстояние) приведены в стандартах DIN 3963, DIN 58405, DIN 3962 Т2, DIN 3967, DIN 3964.

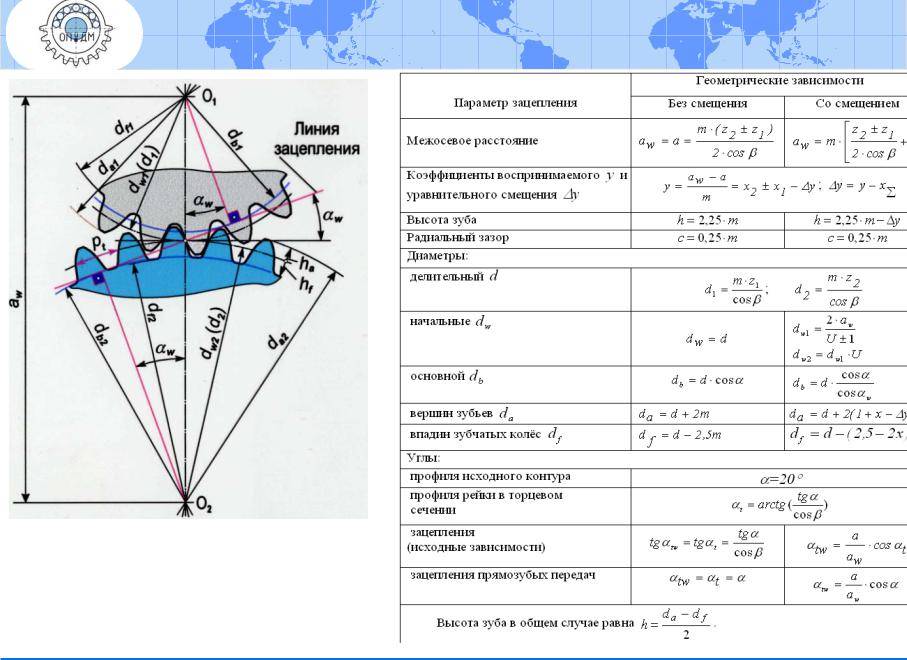
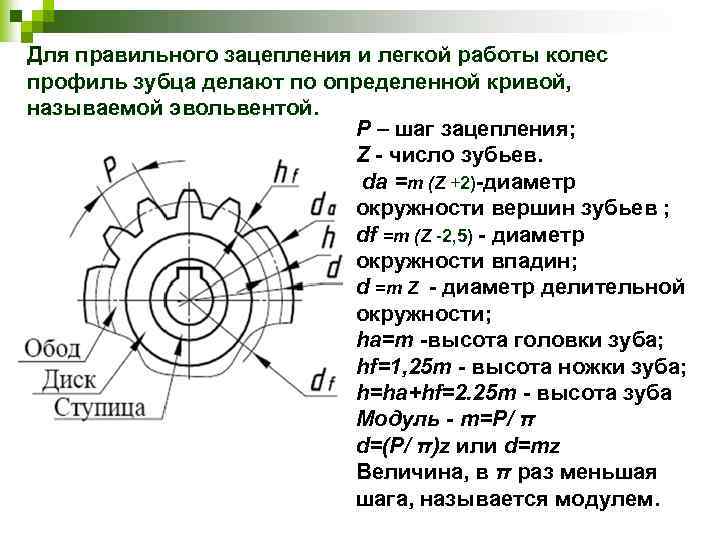
Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Расчет модуля зубчатого колеса

Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

проведя преобразование, получим:

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

выполнив преобразование, находим:

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов D_e получается равным

где h’- высота головки.

Высоту головки приравнивают к m:

Проведя математические преобразования с подстановкой, получим:

Диаметр окружности впадин D_i соответствует D_e за вычетом двух высот основания зубца:

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

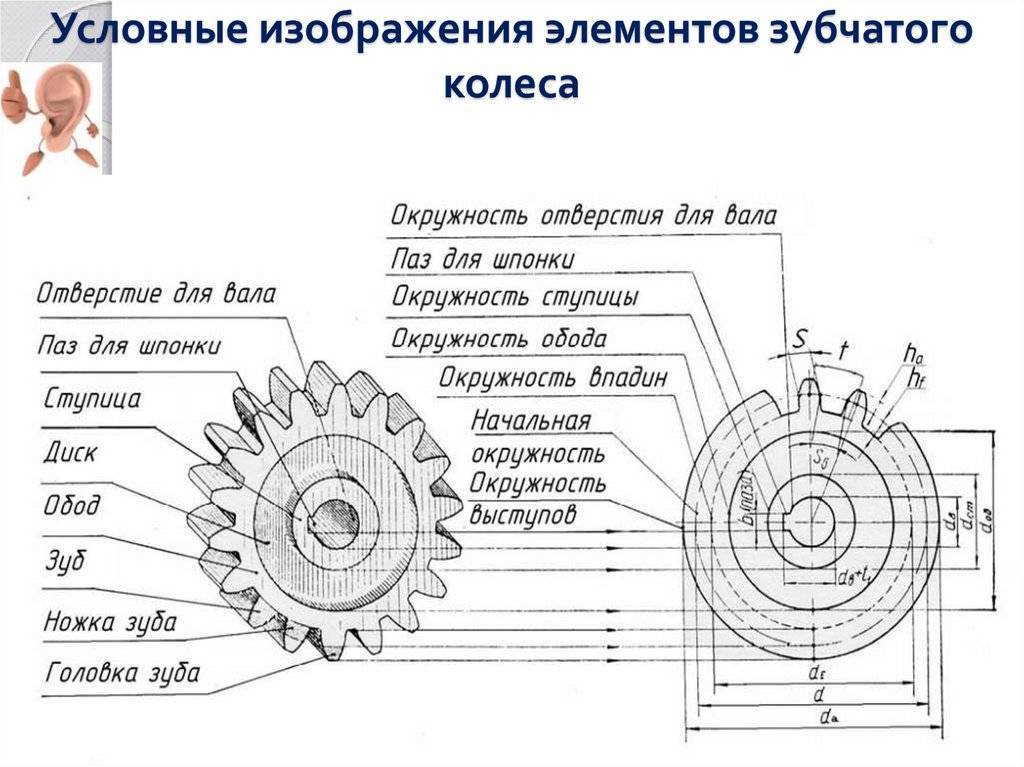
Устройство зубчатого колеса

Выполнив подстановку в правой части равенства, имеем:

что соответствует формуле:

и если выполнить подстановку, то получим:

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины s_в, получаем формулы для ширины впадины

• для отлитых зубцов: s_в=πm-1,53m=1,61m:
• для выполненных путем фрезерования- s_в= πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

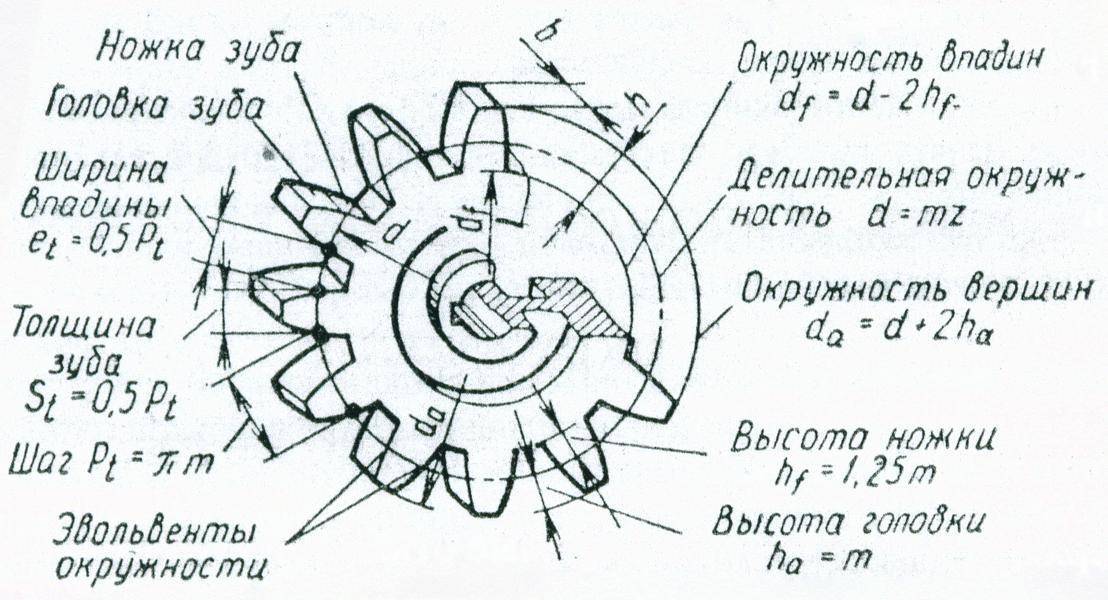
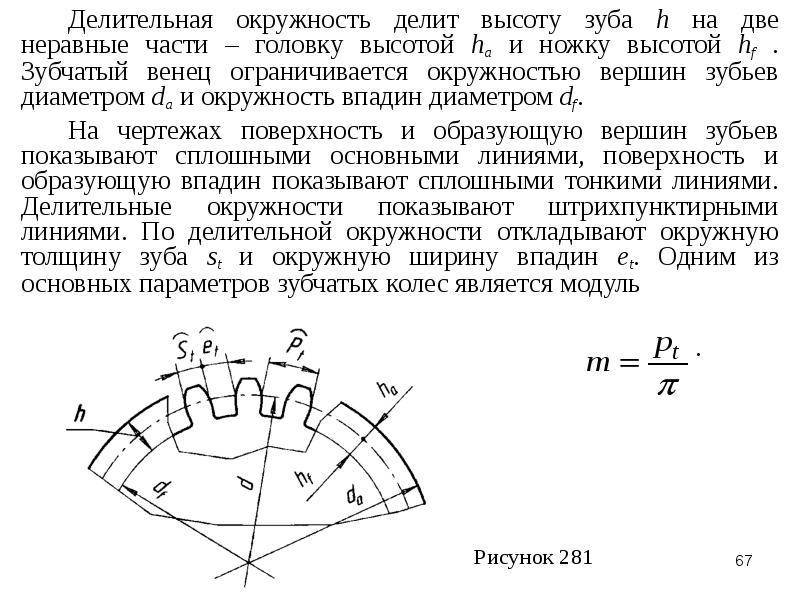
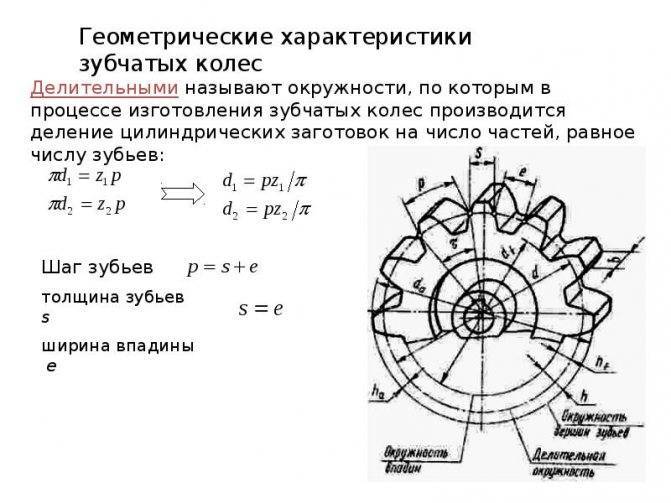
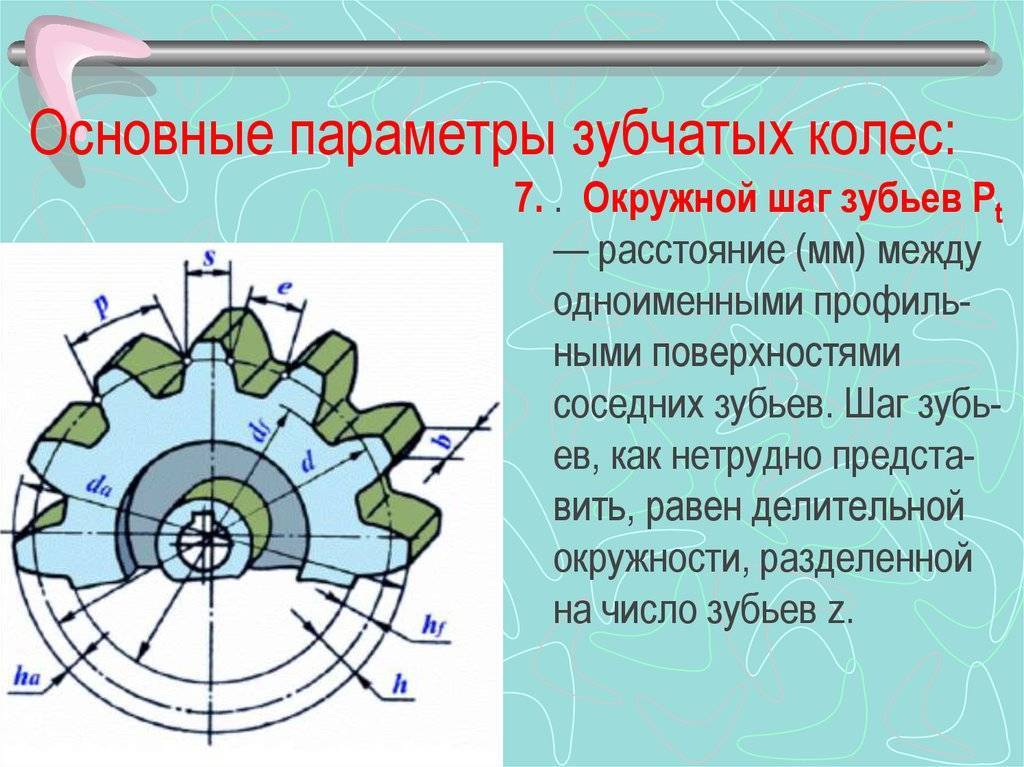
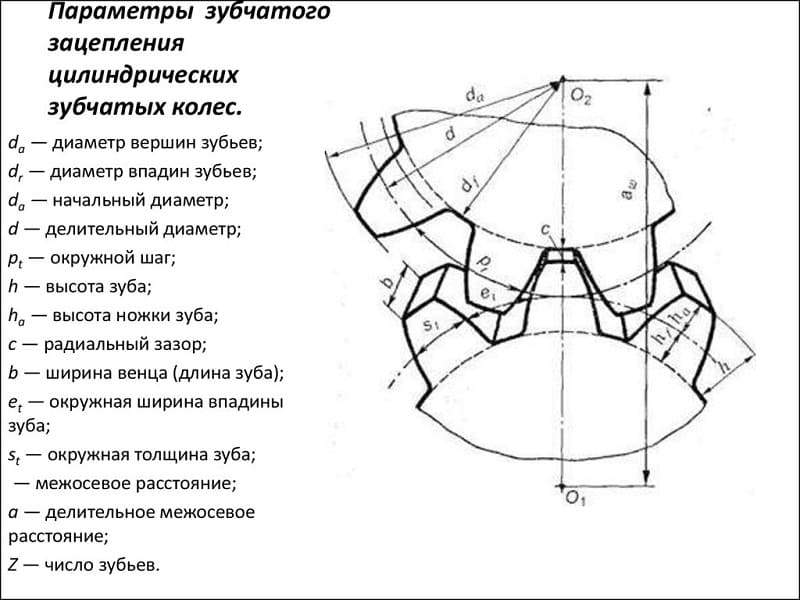
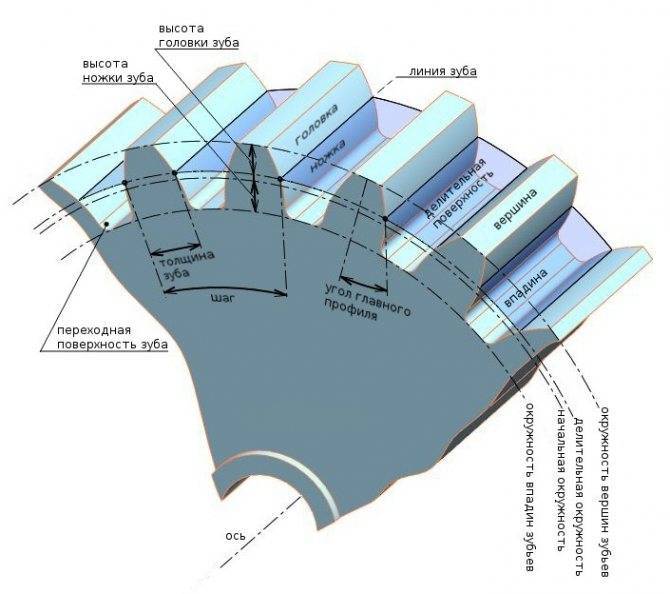
Основные параметры

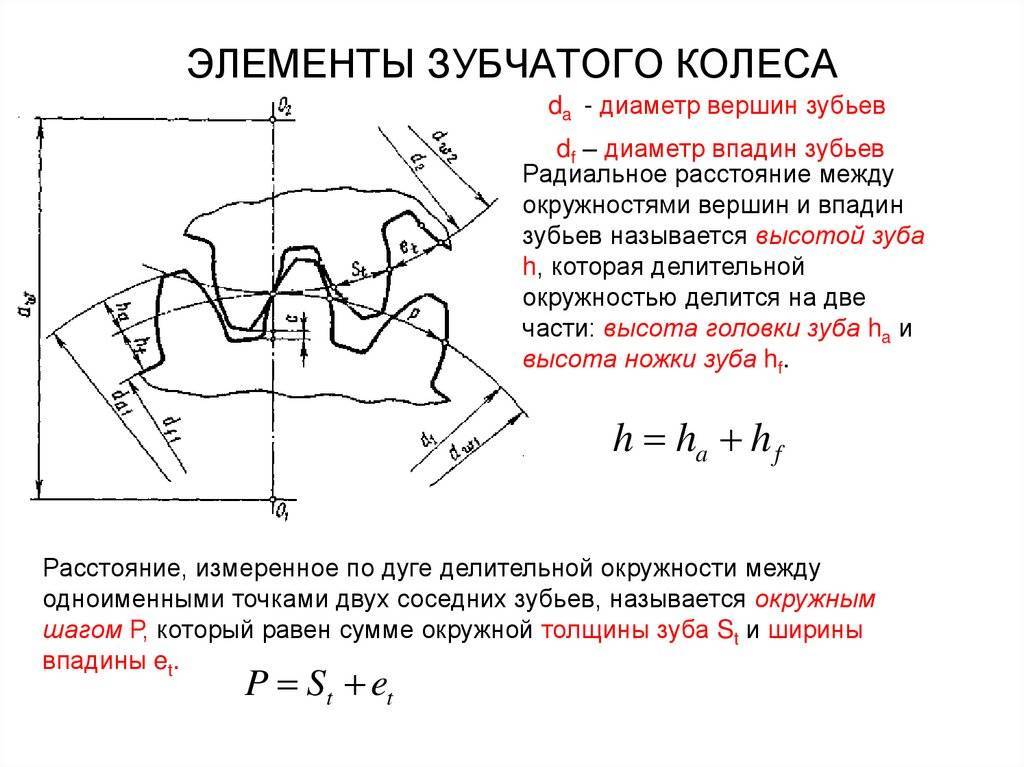
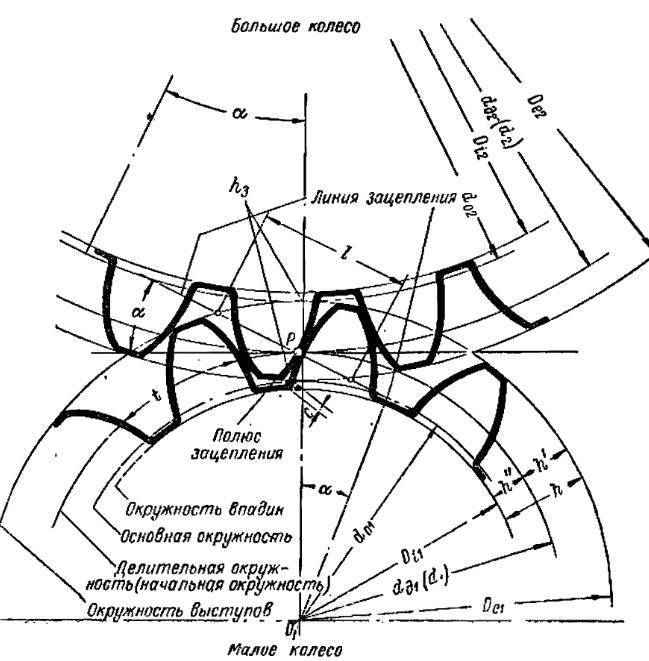
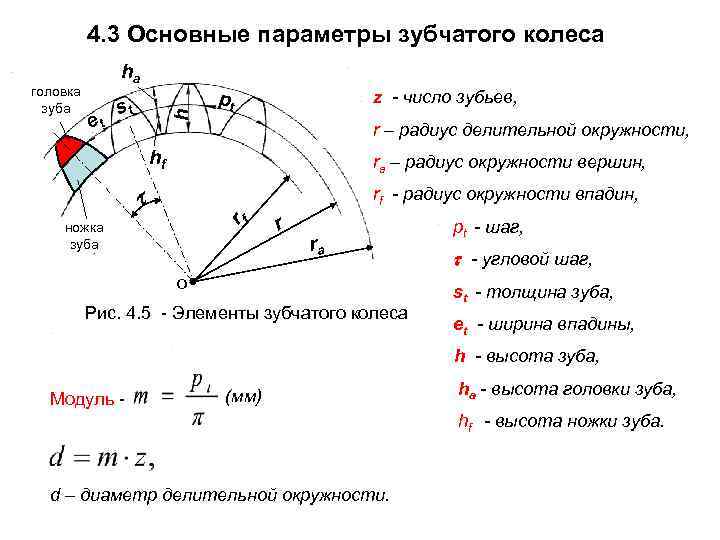
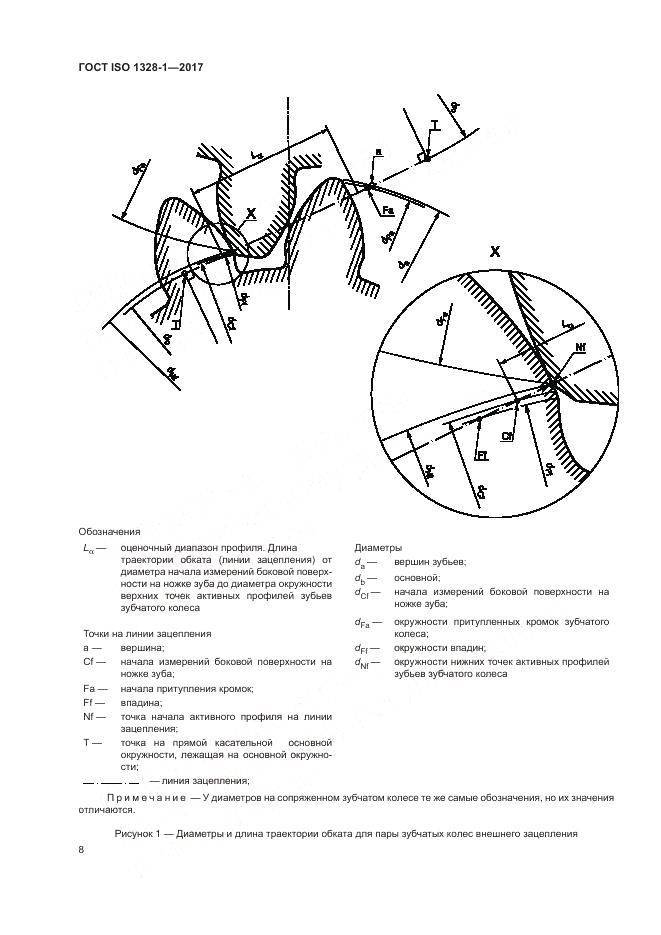
Для обеспечения подвижности и работоспособности, конструкция отдельных деталей механической передачи должна быть согласована по размерам и геометрии. Для этого при описании подобных устройств принято использовать систему специальных параметров. В их число входят геометрические, массогабаритные и прочностные величины, закрепленные стандартами. Применение стандартных параметров позволяет сравнительно просто производить расчет унифицированных зубчатых передач и обеспечивает гарантированное сопряжение всех изделий между собой. Естественно, что для разных видов, параметры будут несколько отличаться. Далее рассматриваются термины, связанные с конструкцией эвольвентного цилиндрического колеса. Эти параметры, в своем большинстве, описывают основные характеристики и других вариантов колес.

В основе сечения зуба большинства шестерен лежит эвольвентный профиль, который  получается на основе одноименной кривой. Его применение легко стандартизируется,  характеризуется высокой технологичностью изготовления и низкими требованиями к качеству сборки механизма. Основными параметры эвольвентного зубчатого колеса  считаются модуль зацепления и количество зубьев зубчатого колеса. При одном и том же наружном диаметре деталей значения этих величин могут существенно отличаться в разных вариантах конструкции.

Число зубьев определяет коэффициент передачи и геометрические размеры зубьев. На ведущем колесе редуктора оно выполняется меньшим, чем на ведомом. В итоге один нормальный оборот ведущей шестерни приводит к повороту ведомого колеса только на определенный угол. Отношение числа зубьев двух колес  дает значение передаточного коэффициента. Размеры зубьев определяются как отношение их количества к длине окружности колеса. С целью упрощения расчетов и гарантированного обеспечения зацепления между разными колесами, предусмотрен дополнительный параметр, называемый модулем зацепления. Любые шестерни с одинаковым модулем обеспечивают взаимодействие между собой и могут использоваться для построения механизмов, без дополнительной обработки.

Сумма ширины зуба и впадины совместно дают шаг зубчатого колеса. Учитывая неравномерность профиля по радиусу и зависимость длины дуги от диаметра, в каждом колесе можно определить бесконечное число значений этого параметра. С целью стандартизации принято рассматривать шаг по делительной окружности, называемый так же окружным шагом. Отношение этого шага к числу пи дает модуль зацепления. В некоторых случаях для описания шестерен используют угловой шаг,  измеряемый в градусах. Стандартами предусмотрены и несколько других угловых величин. Например, для упрощения настройки оборудования при изготовлении колес рассматривают угловую ширину зуба и угловую ширину впадины. Определяются они также на основе делительной окружности.

Зубчатые передачи стартера

Система допускаемых отклонений для зубчатых передач по «Стандарту межосевых расстояний» (DIN 3961) применяется в сило­вых приводах, где требуемый зазор между зубьями обеспечивается отрицательными допусками толщины зубьев. Эта система неприменима для зубчатых передач автомо­бильных стартеров, поскольку они работают со значительно большими зазорами между зубьями, которые обеспечиваются увеличе­нием межосевого расстояния.

Модули зубчатых передач стартеров

Большой крутящий момент, необходимый для пуска двигателя, требует применения зубчатой передачи с большим передаточным отношением (i = 10-20). Поэтому шестерня стартера имеет малое количество зубьев (z = 9-11), обычно с положительным смещением. Для шага зубьев принято следующее обозна­чение: количество зубьев, равное, например, 9/10, означает нарезку девяти зубьев на за­готовке, рассчитанной по диаметру на 10 зу­бьев, и соответствует смещению +0,5. При этом допускаются небольшие отклонения величины коэффициента х. (Это обозначе­ние нельзя смешивать с обозначением Р 8/10, приведенным ниже).

Как рассчитать передаточное число

Шестерня и колесо имеют разное количество зубов с одинаковым модулем и пропорциональный размер диаметров. Передаточное число показывает, сколько оборотов совершит ведущая деталь, чтобы провернуть ведомую на полный круг. Зубчатые передачи имеют жесткое соединение. Передающееся количество оборотов в них не меняется. Это негативно сказывается на работе узла в условиях перегрузок и запыленности. Зубец не может проскользнуть, как ремень по шкиву и ломается.

Расчет без учета сопротивления

В расчете передаточного числа шестерен используют количество зубьев на каждой детали или их радиусы.

Где u12 – передаточное число шестерни и колеса;

Z2 и Z1 – соответственно количество зубьев ведомого колеса и ведущей шестерни.

Важные замечания.

Смещение исходного контура при нарезке зубьев применяют для восстановления изношенных поверхностей зубьев колеса, уменьшения глубины врезания на валах-шестернях, для увеличения нагрузочной способности зубчатой передачи, для выполнения передачи с заданным межосевым расстоянием не равным делительному расстоянию, для устранения подрезания ножек зубьев шестерни и головок зубьев колеса с внутренними зубьями.

Различают высотную коррекцию ( x_Σ(d) =) и угловую ( x_Σ(d) ≠).

Смещение производящего контура на практике применяют обычно при изготовлении прямозубых колес и очень редко косозубых. Это обусловлено тем, что по изгибной прочности косой зуб прочнее прямого, а необходимое межосевое расстояние можно обеспечить соответствующим углом наклона зубьев. Если высотную коррекцию изредка применяют для косозубых передач, то угловую практически никогда.

Косозубая передача работает более плавно и бесшумно, чем прямозубая. Как уже было сказано, косые зубья имеют более высокую прочность на изгиб и заданное межосевое расстояние можно обеспечить углом наклона зубьев и не прибегать к смещению производящего контура. Однако в передачах с косыми зубьями появляются дополнительные осевые нагрузки на подшипники валов, а диаметры колес имеют больший размер, чем прямозубые при том же числе зубьев и модуле. Косозубые колеса менее технологичны в изготовлении, особенно колеса с внутренними зубьями.

Подписывайтесь на анонсы статей в окнах, расположенных в конце каждой статьи или вверху каждой страницы.

Прошу уважающих труд автора скачивать файл после подписки на анонсы статей!

Ссылка на скачивание файла: modul-zubchatogo-kolesa (xls 41,0KB).