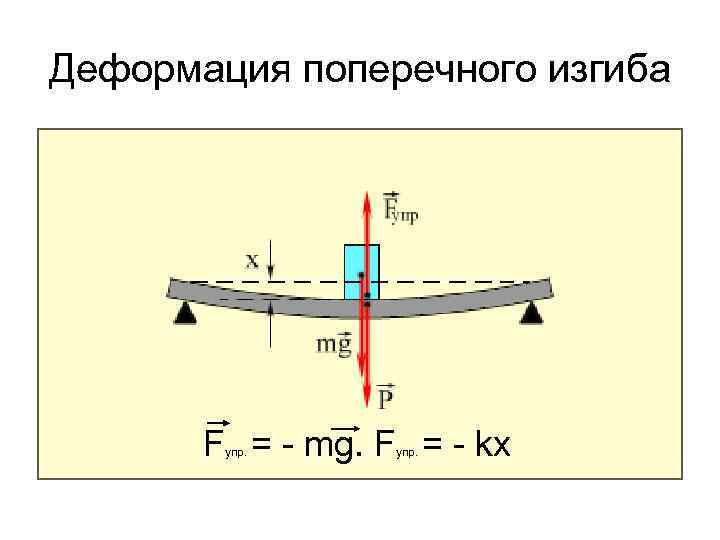
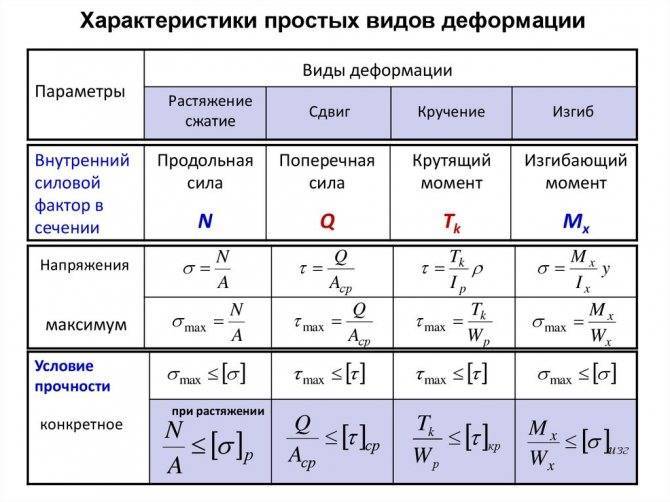
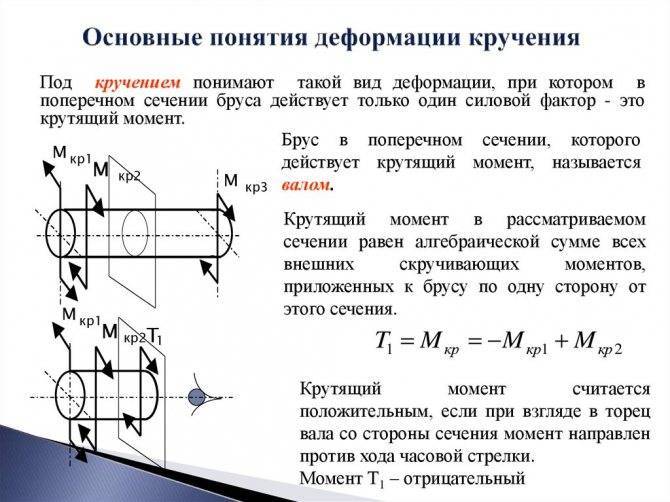
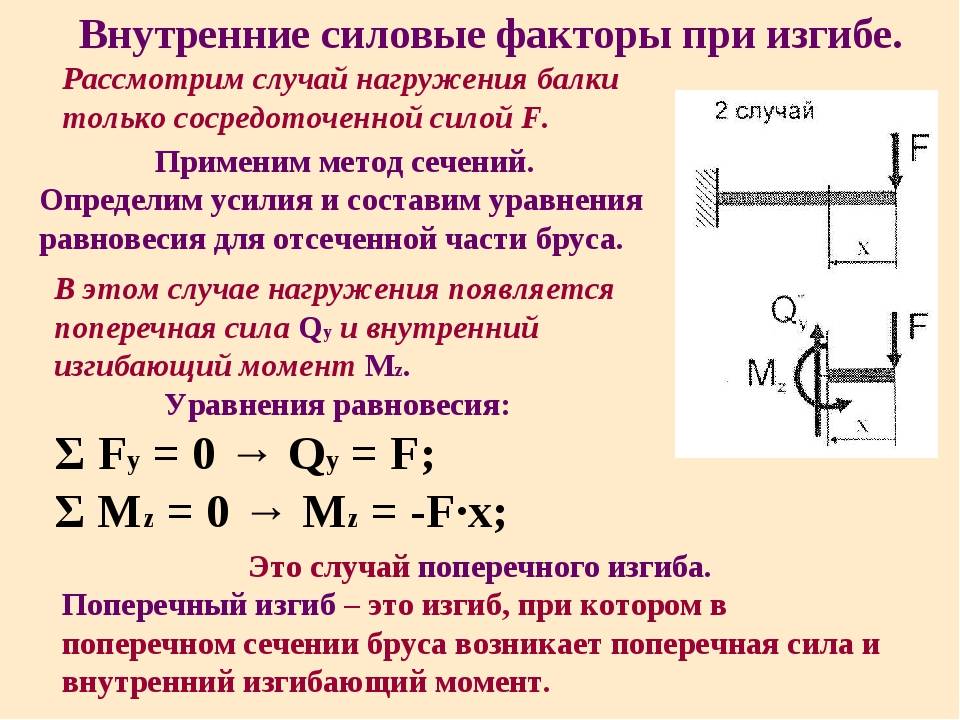
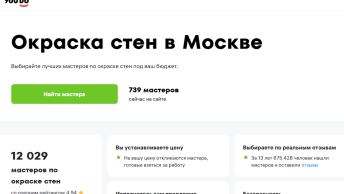
Интенсивная пластическая деформация
Получить беспористые объемные металлические наноматериалы можно технологиями интенсивной пластической деформации (ИПД). Их суть заключается в деформировании металлических заготовок:
- при относительно небольших температурах;
- при повышенном давлении;
- с высокими степенями деформации.
Это обеспечивает формирование гомогенной наноструктуры с большеугловыми границами зерен. Вопреки интенсивному воздействию, образцы не должны получать механические повреждения и разрушаться.
Технологии ИПД:
- кручение (ИПДК);
- разноканальное угловое прессование;
- всесторонняя ковка;
- мультиосевое деформирование;
- знакопеременный изгиб;
- аккумулированная прокатка.
Первые работы по созданию наноматериалов выполнены в 80х-90х годах ХХ века с использованием методов кручения и разноканального прессования. Первый метод применим для небольших образцов – получаются пластинки диаметром 10…20 мм и толщиной до 0,5 мм. Для того чтобы получить массивные наноконструкции используется второй метод, в основу которого положена деформация сдвигом.
Они высокопроизводительные, позволяют обеспечить требуемое качество получаемых изделий, улучшить их механические свойства.
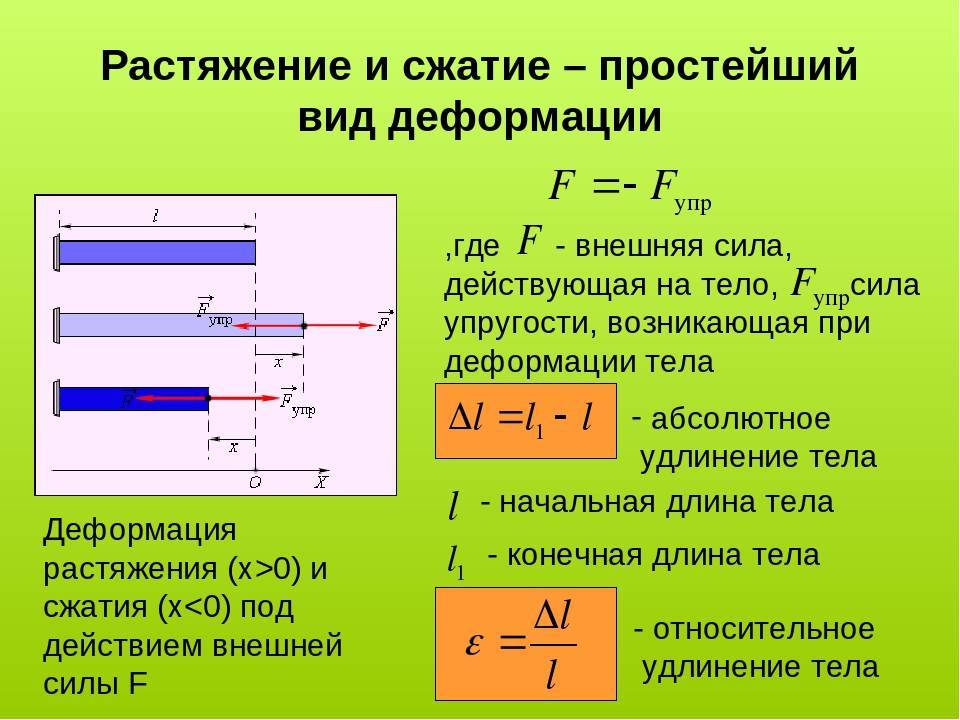
Механическое напряжение
Определение 4
Механическое напряжение твердого тела σ – это показатель, равный отношению модуля внешней силы к площади сечения твердого тела.
σ=FS.
Величину механического напряжения принято выражать в паскалях (Па) и измерять в единицах давления.
Важно понимать, как именно механическое напряжение и относительная деформация связаны между собой. Если отобразить их взаимоотношения графически, мы получим так называемую диаграмму растяжения. При этом нам нужно отмерить величину относительной деформации по оси x, а механическое напряжение – по оси y
На рисунке ниже представлена диаграмма растяжения, типичная для меди, мягкого железа и некоторых других металлов
При этом нам нужно отмерить величину относительной деформации по оси x, а механическое напряжение – по оси y. На рисунке ниже представлена диаграмма растяжения, типичная для меди, мягкого железа и некоторых других металлов.
Рисунок 3.7.2. Типичная диаграмма растяжения для пластичного материала. Голубая полоса – область упругих деформаций.
В тех случаях, когда деформация твердого тела меньше 1% (малая деформация), то связь между относительным удлинением и механическим напряжением приобретает линейный характер. На графике это показано на участке Oa. Если напряжение снять, то деформация исчезнет.
Определение 5
Деформация, исчезающая при снятии напряжения, называется упругой.
Линейный характер связи сохраняется до определенного предела. На графике он обозначен точкой a.
Определение 6
Предел пропорциональности – это наибольшее значение σ=σпр, при котором сохраняется линейная связь между показателями σ и ε.
Слишком сложно? Не парься, мы поможем разобраться и подарим скидку 10% на любую работу
Опиши задание
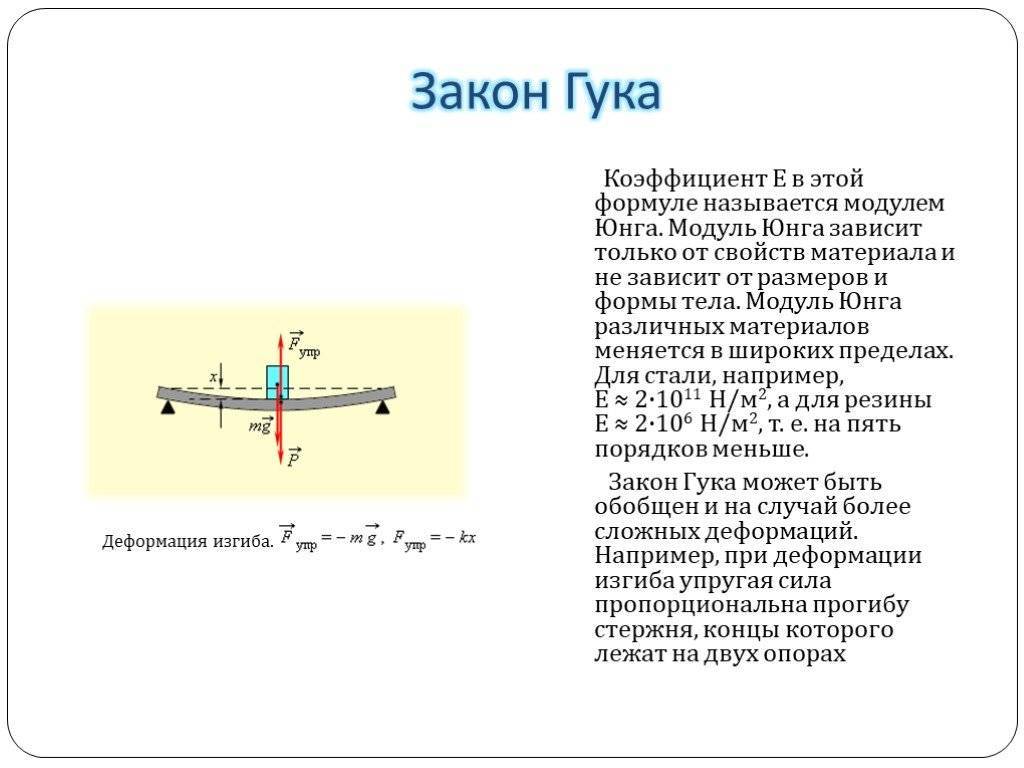
На данном участке будет выполняться закон Гука:
ε=1Eσ.
В формуле содержится так называемый модуль Юнга, обозначенный буквой E.
Если мы продолжим увеличивать напряжение на твердое тело, то линейный характер связи нарушится. Это видно на участке ab. Сняв напряжение, мы также увидим практически полное исчезновение деформации, то есть восстановление формы и размеров тела.
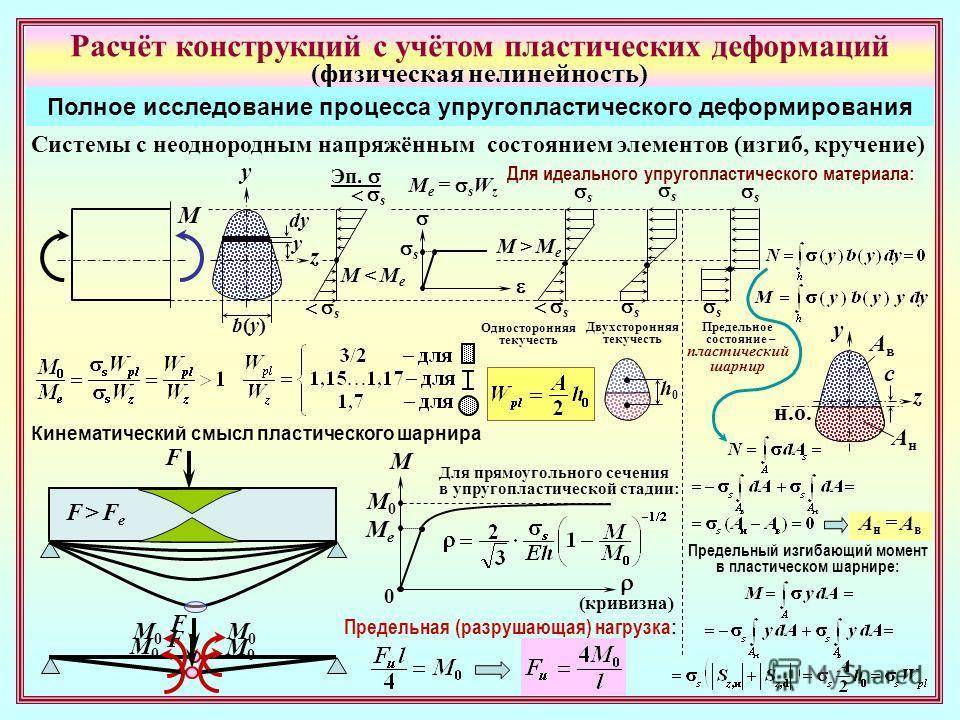
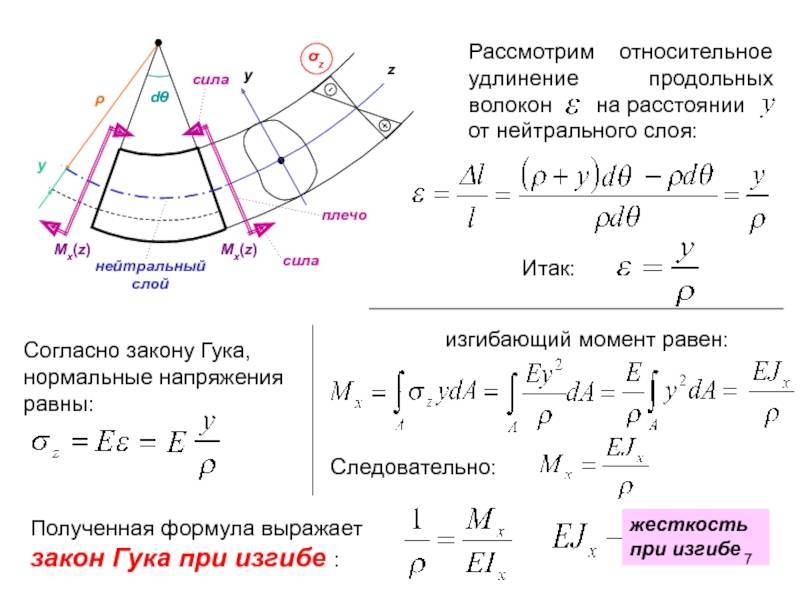
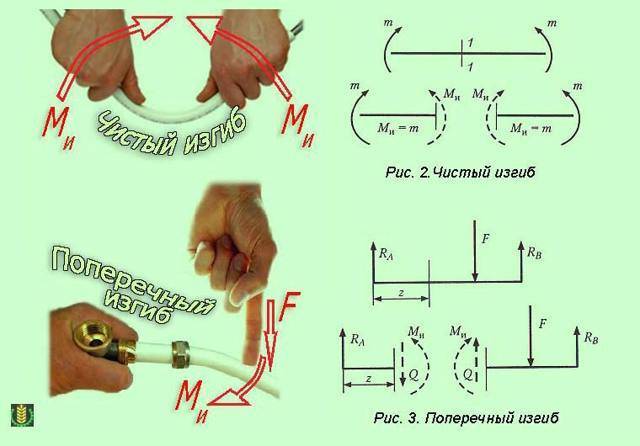
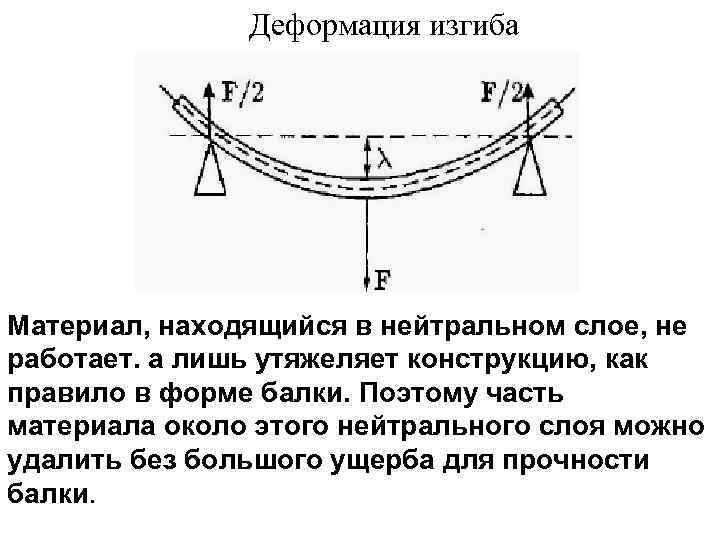
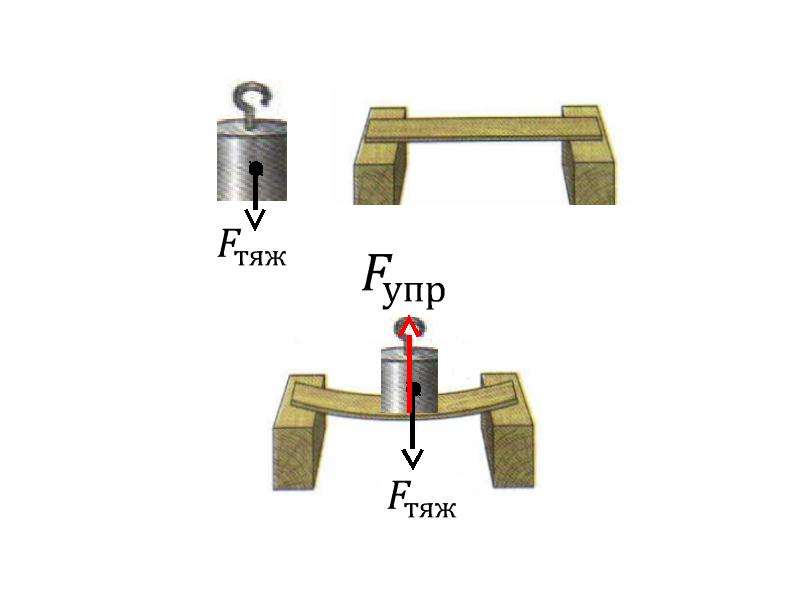
Изгибающий момент и поперечная сила
Для оценки показателей деформационных процессов, которые протекают в самых разнообразных конструкциях, используют изгибающий момент и воздействующую поперечную силу. Их рассчитывают на основании уравнений равновесия. Каждое дает возможность найти параметры каждого слоя балки при изгибе.
Во время проектирования конструкции для расчёта таких параметров берут во внимание следующие правилами:
влияние внешнего фактора, способного повернуть балку по часовой стрелке относительно проведенного сечения;
образовывается изгибающий момент, который может привести к сжатию любого из волокон балки (в уравнении его берут во внимание со знаком плюс);
Полученные результаты дают возможность построить графическое изображение распределения сил и факторов на самых разных уровнях. Такие изображения называют эпюрами. При их помощи формируют крепость создаваемой конструкции.
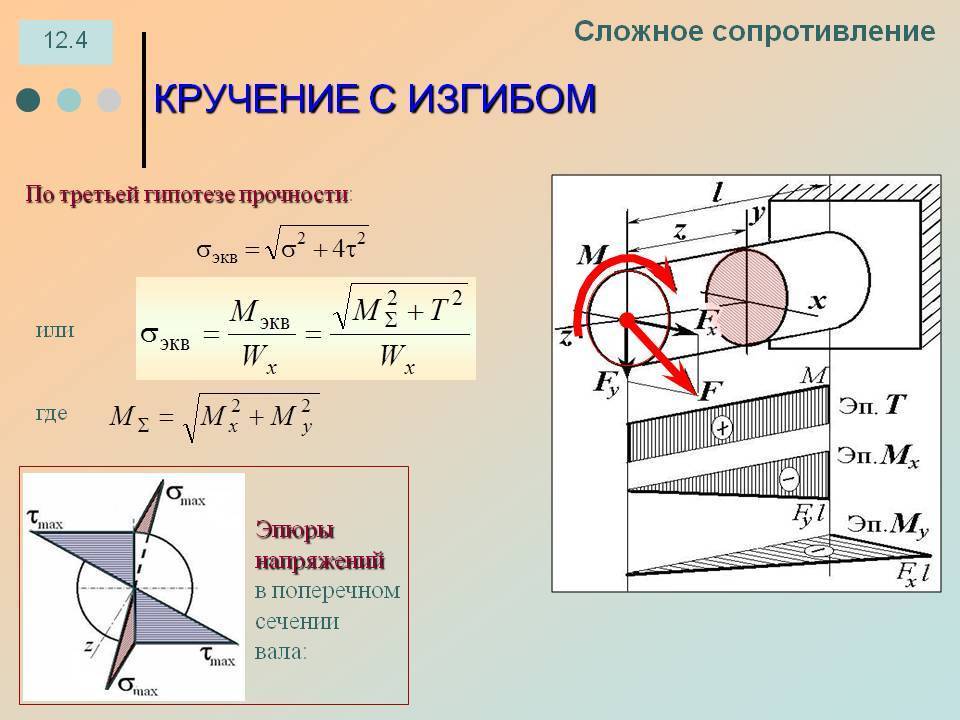
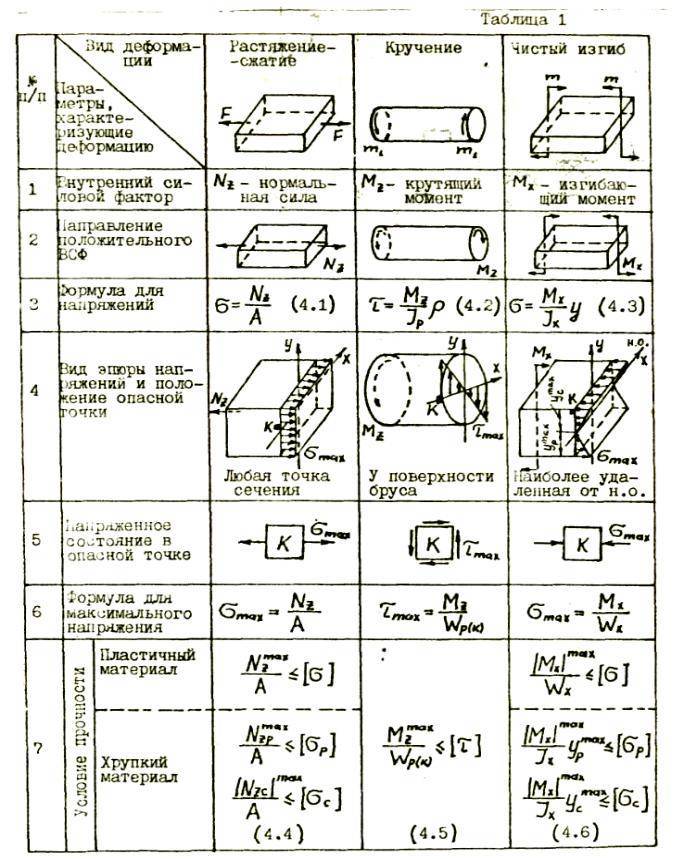
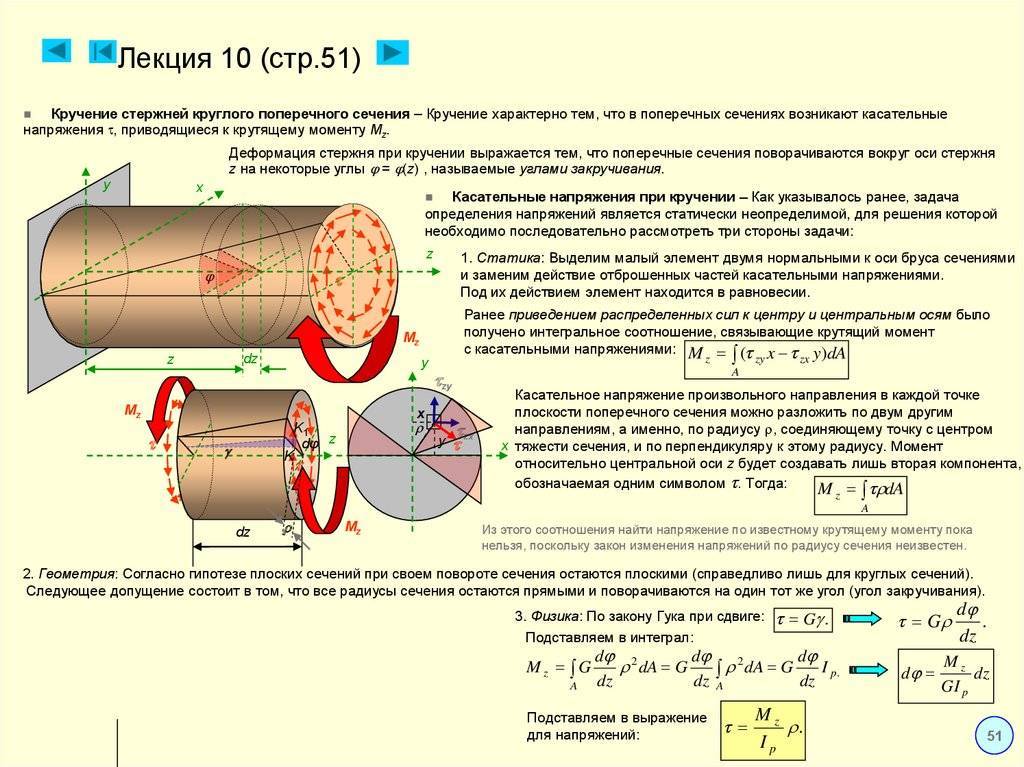
Напряжения кручения
Исходя из приведенного выше определения деформации кручения, при данном процессе в поперечном сечении наблюдаются лишь касательные напряжения, направленные перпендикулярно к радиусам. Их определяют для конкретной точки как произведение соотношения крутящего момента к геометрическому полярному инерционному моменту и расстояния данной точки от оси кручения.
Изменение касательных напряжения линейно, и максимальной величины они достигают на поверхности при наибольших значениях крутящего момента и расстояния от оси кручения, поэтому ее значение вычисляют как частное наибольшего крутящего и полярного моментов сопротивления.
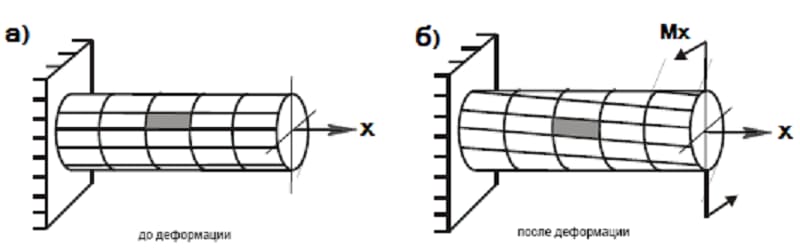
С применением данного условия возможно вычислить прочие параметры: по силовым факторам, создающим крутящий момент – показатель сопротивления и далее размеры сечения в зависимости от формы, либо по размеру сечения – максимально допустимое для него значение крутящего момента и на основе последней допустимые значения внешних нагрузок.
Касательные напряжения, по закону парности, формируются при кручении как в поперечных, так и в продольном направлениях. Вследствие этого во всех точках вала наблюдается деформация в виде чистого сдвига. Главные напряжения направлены к образующей под углом 45°.
Помимо скручивающих усилий возможно воздействие на вал моментной нагрузки.
Из изложенных выше данных следует, что удаление материала в районе оси вала незначительно сказывается на прочности ввиду того, что данная часть мало нагружена. При равных площади сечения и массе деталей кольцевые варианты характеризуются большими полярными моментами сопротивления и инерции по сравнению со сплошными валами. То есть при равной массе полые варианты прочнее и жестче, а при одинаковых показателях прочности и жесткости легче. Названные параметры определяют устойчивость данных изделий к деформации.
Выше были рассмотрены особенности деформации кручения круглых в поперечном разрезе предметов. Для треугольных, прямоугольных, эллиптических и прочих вариантов не применима гипотеза плоских сечений. Это обусловлено тем, что поверхности данного типа при кручении искривляются. Данный процесс их коробления вследствие смещения отдельных точек при деформации вдоль оси называют депланацией. Вследствие этого методы сопротивления материалов для вычисления кручений и напряжений неприменимы. Вместо них используют методы теории упругости.
Для изделий произвольной поперечной формы касательные напряжения имеют направление по касательной к контуру, однако при наличии внешних углов они отсутствуют. Так, при разложении напряжения вблизи угла по нормалям к его сторонам надвое из закона парности следует формирование касательных напряжений на свободной поверхности. Однако в данном случае она свободна от нагрузки, поэтому у внешнего угла касательные напряжения обнуляются.
Для наиболее распространенных среди вариантов некруглого сечения прямоугольных валов наибольшие напряжения характерны для поверхностных участков в середине длинных сторон. Следовательно, там наблюдается наибольшая деформация кручения.
Прямоугольные детали в сравнении с круглым характеризуются значительно меньшими жесткостью и прочностью. Причем это отличие увеличивается с ростом отношения сторон. Следовательно, они более подвержены деформации.
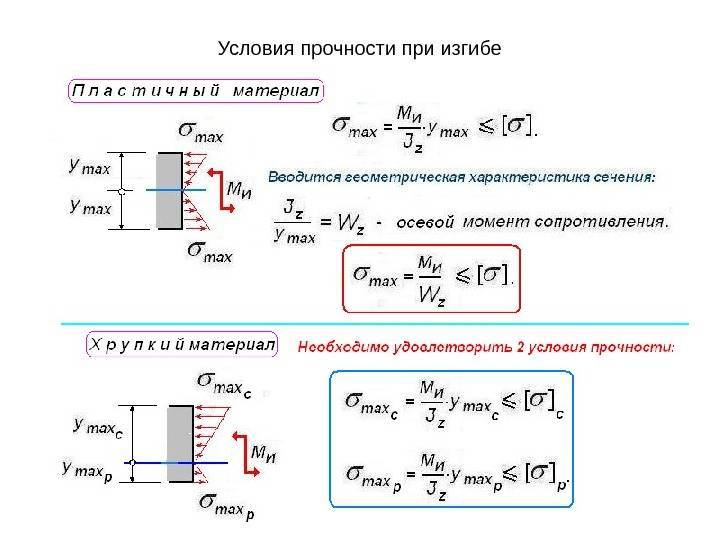
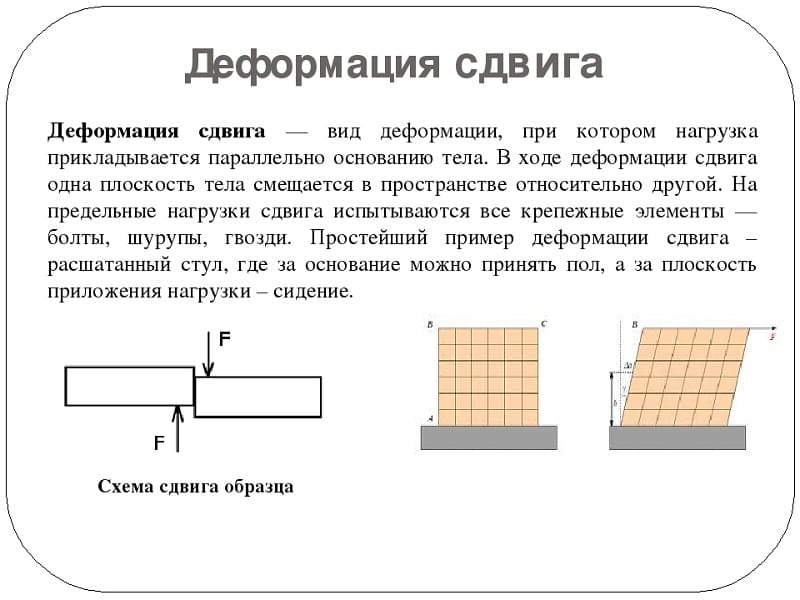
Расчёты на прочность при сдвиге
Оценка прочностных характеристик изделий производится для определения наступления трёх моментов деформации:
- Смещение отдельных слоёв (появления угла деформации).
- Смятие элементов крепления.
- Сдвиг.
- Разрыв.
Расчёт на прочность необходим для определения условий наступления каждого из видов. На практике для более наглядной оценки характеристик прочности и стойкости к деформации решают существующие аналитические выражения и изображают эпюры отражающие направления воздействия различных видов напряжений.
Получение численных характеристик возможно благодаря применению разработанных методов решения систем дифференциальных уравнений. Уточнение аналитических выражений производится на основе принятых гипотез.
Расчёт допустимых напряжений производится на основании первой, третьей и четвёртой гипотезы прочности. Каждая из гипотез принимается для различных материалов, обладающих своими физико-механическими характеристиками.
Прочность находиться на каждом из этапов разработки конкретной детали. Сначала вычисляют величины допустимых напряжений и угол отклонения на предварительном (проверочном) этапе. Это позволяет определить их уровни, величины и направление приложенных сил. После этого приступают к проектированию. На этом этапе производится выбор материала детали и крепёжных элементов с учётом необходимой прочности каждого элемента конструкции. На конечном этапе ещё раз проверяют допустимые нормы нагрузки и способность готовой детали выдерживать допустимую и дополнительную нагрузку, то есть определяют запас прочности.
Наиболее показательными являются расчёты для чистого сдвига. В этом случае при расчёте рассматривают следующие аспекты решения задачи:
- Статический (составляется уравнение равновесия). В этом случае используется предположение о равномерности распределения касательных напряжений. Однако в некоторых случаях они распределяются не равномерно, что усложняет решение поставленной задачи. Он позволяет установить связь возникших напряжений с действующими внешними силами. Это производиться благодаря получению семейства решений дифференциальных уравнений равновесия для всего объёма детали.
- Геометрический (деформационный). Позволяет отобразить связь между отдельными небольшими участками исследуемой детали.
- Математический. Позволяет выбрать метод решения составленной системы уравнений. Провести математическое моделирование протекающих процессов.
- Физический. Устанавливает связь между физическими процессами при деформации с учётом физических свойств материала и возникшими напряжениями (механическими свойствами).
На математическом и физическом этапе рассмотрения поставленной задачи применяются следующие основные расчетные выражения и допущения:
- закон Гука для деформации смещения;
- гипотезы прочности (с учётом физических и механических свойств выбранного материала);
- выбор системы эквивалентных напряжений;
- упрощения при изображении эпюр, отображающих направления действующих сил и возникших напряжений;
- принятие основных положений для случая чистого сдвига.
В первом случае происходит пластическая деформация детали, когда интенсивность возникших напряжений превышает предел текучести выбранного материала. Размеры такой деформации зависят от характера и интенсивности действия внешних сил, показателей прочности материала, изменения температурного режима.
При интенсивности воздействия, превышающем прочность материала, происходит разрыв. Оба эти процесса приводят к нарушению механических соединений деталей (например, метизов, заклёпок, втулок).
Разработанные методы расчёта прочности позволяют проектировать и изготавливать детали с заданием, превышающим этот предел. Это позволяет существенно повысить надёжность и долговечность всей конструкции. В настоящее время разработан стройный математический аппарат создания моделей допустимой деформации. Его реализуют с применением созданных программных средств, которые позволяют получить числовые характеристики прочности и построить графические изображения эпюр в формате 3D графики.
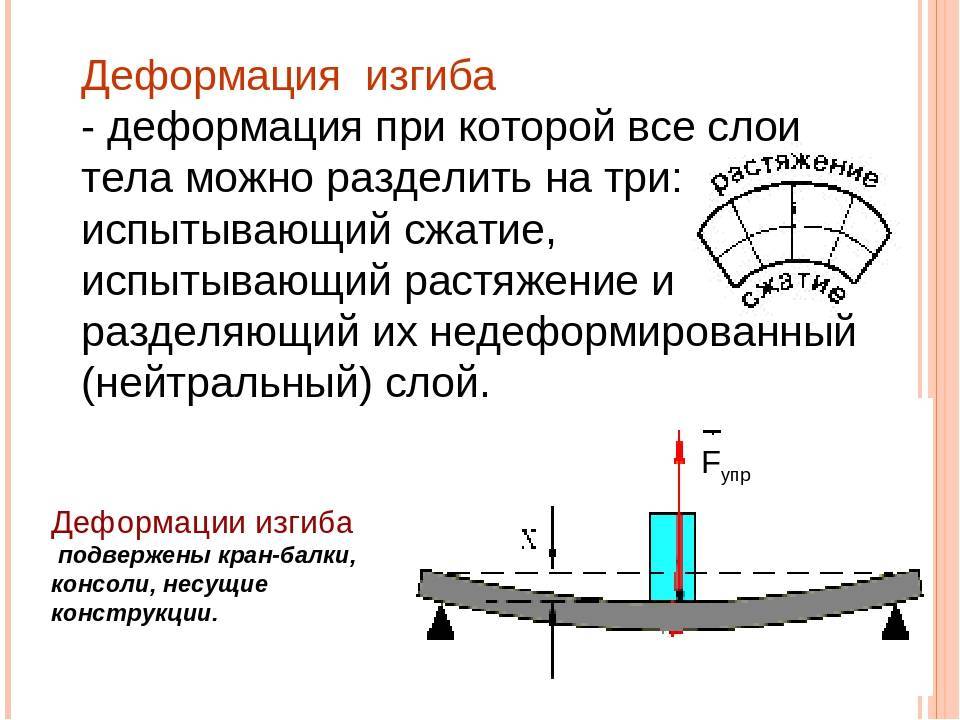
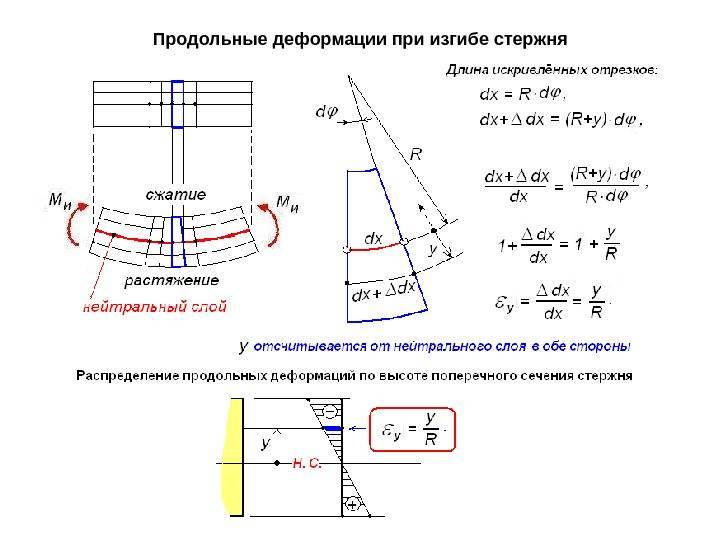
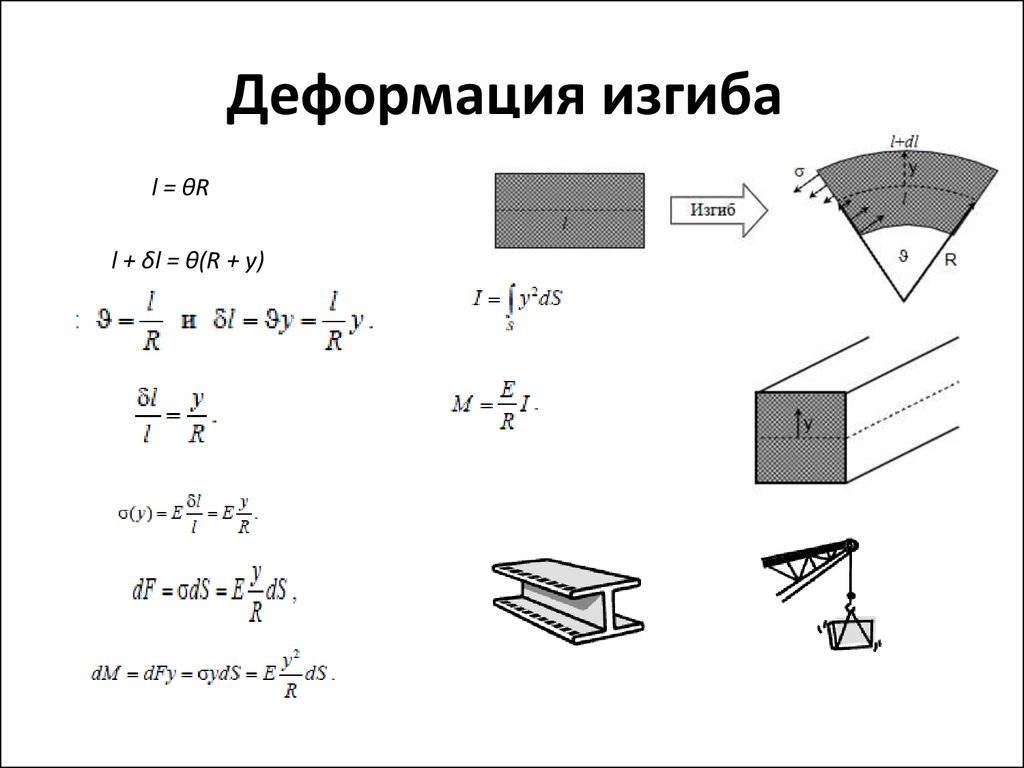
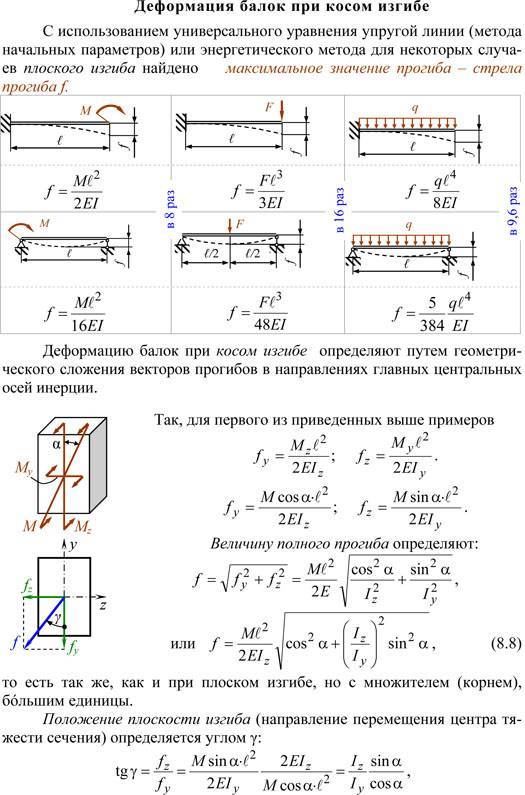
Определение деформаций при изгибе
Касательная к оси кривой стержня в любой точке стержня находится под углом, равным углу поворота сечения в этой точке относительно исходной оси. Тангенс тангенса наклона tg9 = dy / dx. Однако, поскольку фактическое значение угла поворота поперечного сечения при изгибе невелико (порядка 1/1000 радиан), тангенс угла угла равен yuia (tg0 «0), а угол поворота поперечного сечения и зависимости 0 ~ Вы можете найти отношение отклонения в виде dyldx.
Mi> 0 Y Ми <0 О тебе «> у «<О y «> ОМ„ <0 у «<О М> 0 г Рисунок 5.24 Из математического процесса известна следующая зависимость кривизны линии L «в плоскости XOY. K = ± (d2 yIdx2) / (1+ (dy / dx) 2) 3/2. (5,41) Однако, поскольку (dy / dx) 2 = tg20 = b2 «1, формула (5.41) имеет вид K = ± (d2y / dx2). (5,42) Используя зависимость (5.34), соедините кривизну оси стержня с изгибающим моментом Mn и жесткостью сечения E1 {. (5,43) (5,44) K = \ / p = MJ (EIz). Сравнивая уравнения кривизны, полученные в зависимостях (5.42) и (5.43), можно получить дифференциальное уравнение оси изгиба стержня. ± (d2y / dx2) = МДж (EIz),
Его интеграция не сложная. Выбор знака в уравнении (5.44) определяется используемой системой координат. Ранее принятый символ Л / и изгибающего момента (рисунок 5.24, б — е) не зависит от направления осей. Кривизна линии положительна, т. Е. Y «= ^ y / cbc2> 0, когда вогнутая поверхность кривой совпадает с положительным направлением оси ОА (рис. 5.24, б, д), и наоборот (рис. 5.24, в, г) В направлении приема оси ОК знак слева и справа.
Уравнение (5.44) всегда одинаково. Если y «> 0 и Mn> 0, а f ‘
Пример 5.4. Нагрузка приложена к концу силой концентрации F. Жесткость стержня постоянна с длиной, равной EI. Получите начало координат в точке B, которая является жесткой фиксированной точкой стержня. Ось OK направлена вверх, а ось находится справа от OX ~. Для любого сечения на расстоянии x от начала координат изгибающий момент равен L / и = -F (l-x). Дифференциальное уравнение (5.45) оси кривой принимает вид EI (d2y / dx2) -F (l-x).
Интегрирование этого уравнения дает EI (dy / dx) = -F (lx-x2 / 2) + C. При дальнейшей интеграции получается уравнение отклонения. Ely-F (lx2 / 2-x / 6) + Cx + D dO / dx = MK / (EIZ). Чтобы найти уравнения, определяющие деформацию стержней или их угловые и линейные перемещения, необходимо интегрировать уравнение (5.45). После интеграции вы получите уравнение угла поворота Учитывая, что точка взгляда в точке x = 0, прогиб y и угол поворота Q = dy / dx сечения равны нулю, можно видеть, что константы интегрирования C-0 и Z> = 0. Далее свободный конец стержня в точке x = 1 y = -Lg / (ZEG) и угол поворота Q-dy / dx = -Fl2 / (2EI) конца. Знак «-» в представлении угла отклонения и поворота указывает на то, что отклонение выполняется в направлении, противоположном положительному направлению оси OY. Если вы установите его, край будет вращаться по часовой стрелке.
| Определение нормальных напряжений при изгибе | Понятие о теориях прочности |
| Определение касательных напряжений при изгибе | Изгиб с кручением стержней круглого поперечного сечения |
Если вам потребуется помощь по прикладной механике вы всегда можете написать мне в whatsapp.
Испытание на вязкость разрушения
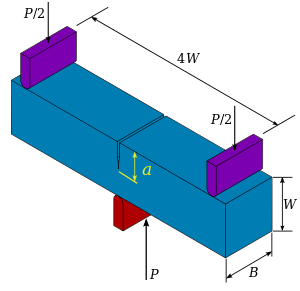
Single-кромочные вырезы -bending образца (также называют три точки изгиба образца) для испытания трещиностойкости.
Вязкость разрушения образца также можно определить , используя тест на трехточечный изгиб. Коэффициент интенсивности напряжений в вершине трещины образца изгиба с одиночным надрезом равен
- Kязнак равно4пBπW1.6(аW)12-2,6(аW)32+12,3(аW)52-21,2(аW)72+21,8(аW)92{\ displaystyle {\ begin {align} K _ {\ rm {I}} & = {\ frac {4P} {B}} {\ sqrt {\ frac {\ pi} {W}}} \ left [1.6 \ left ({\ frac {a} {W}} \ right) ^ {1/2} -2,6 \ left ({\ frac {a} {W}} \ right) ^ {3/2} +12,3 \ left ({ \ frac {a} {W}} \ right) ^ {5/2} \ right. \\ & \ qquad \ left.-21.2 \ left ({\ frac {a} {W}} \ right) ^ {7 /2}+21,8\left({\frac {a} {W}} \ right) ^ {9/2} \ right] \ end {align}}}
где – приложенная нагрузка, – толщина образца, – длина трещины,
– ширина образца. При испытании на трехточечный изгиб усталостная трещина создается на вершине надреза в результате циклического нагружения. Измеряется длина трещины. Затем образец загружается монотонно. График зависимости нагрузки от смещения раскрытия трещины используется для определения нагрузки, при которой трещина начинает расти. Эта нагрузка подставляется в приведенную выше формулу для определения вязкости разрушения .
п{\ displaystyle P}B{\ displaystyle B}а{\ displaystyle a}W{\ displaystyle W}Kяc{\ displaystyle K_ {Ic}}
Стандарты ASTM D5045-14 и E1290-08 предлагают соотношение
- Kязнак равно6пBWа12Y{\ displaystyle K _ {\ rm {I}} = {\ cfrac {6P} {BW}} \, a ^ {1/2} \, Y}
где
- Yзнак равно1,99-аW(1-аW)(2,15-3,93аW+2,7(аW)2)(1+2аW)(1-аW)32.{\ displaystyle Y = {\ cfrac {1,99-a / W \, (1-a / W) (2,15–3,93a / W + 2,7 (а / W) ^ {2})} {(1 + 2a / W ) (1-а / W) ^ {3/2}}} \ ,.}
Прогнозируемые значения практически идентичны для уравнений ASTM и Бауэра для длин трещин менее 0,6 .
Kя{\ displaystyle K _ {\ rm {I}}}W{\ displaystyle W}
