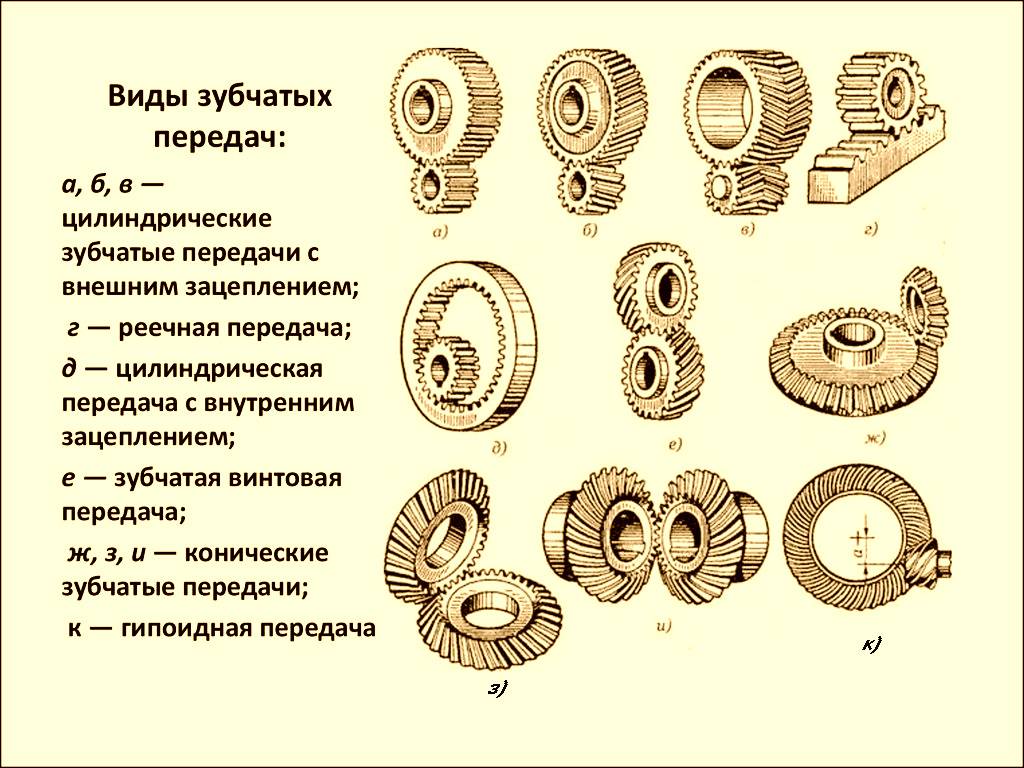
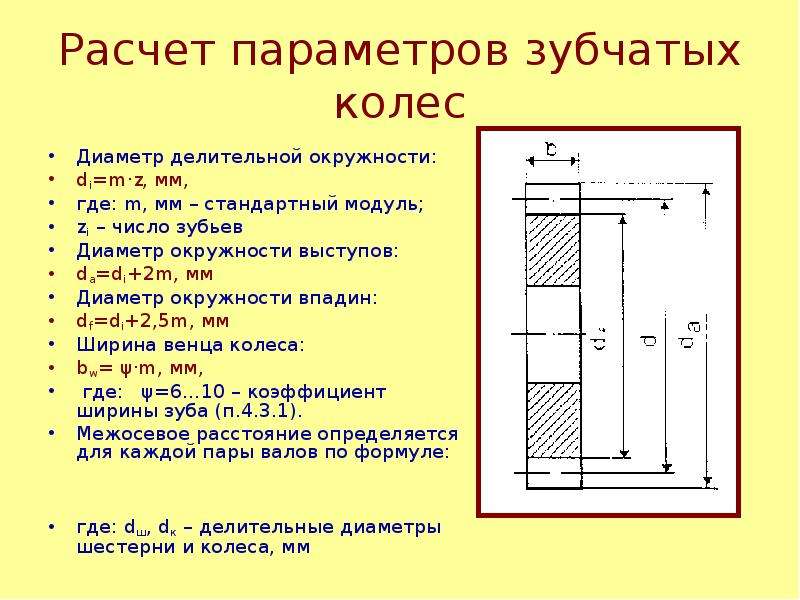
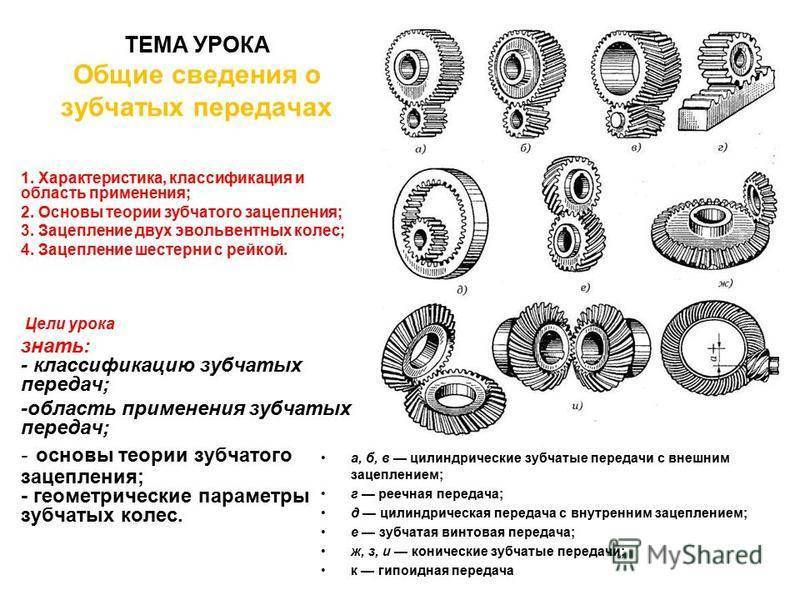
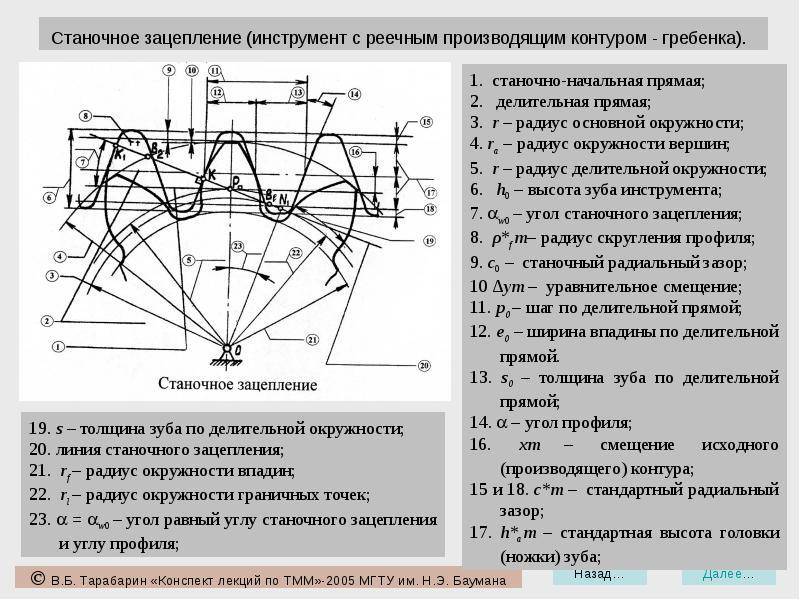
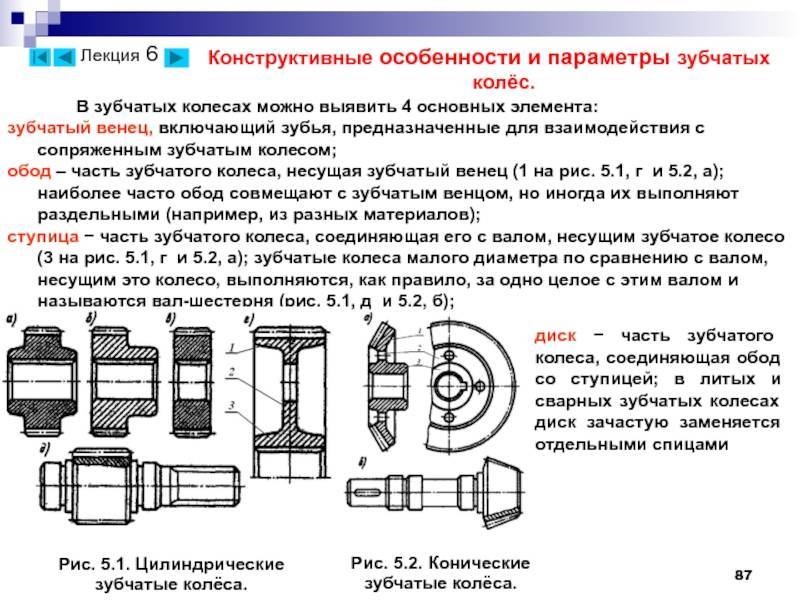
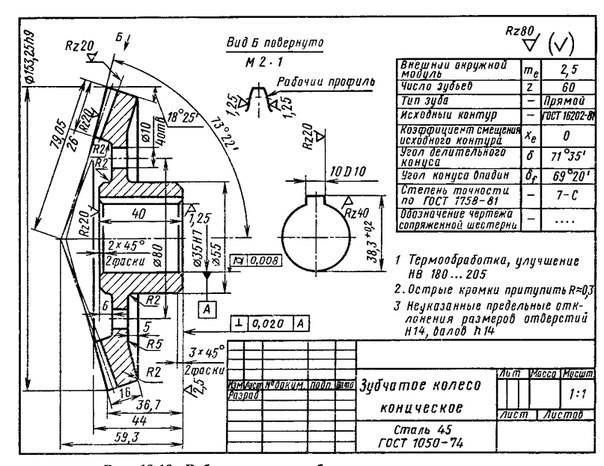
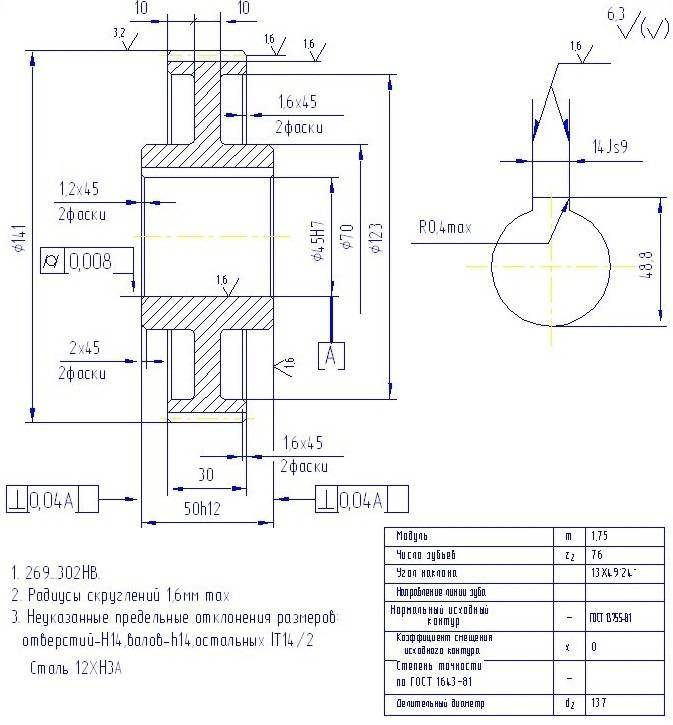
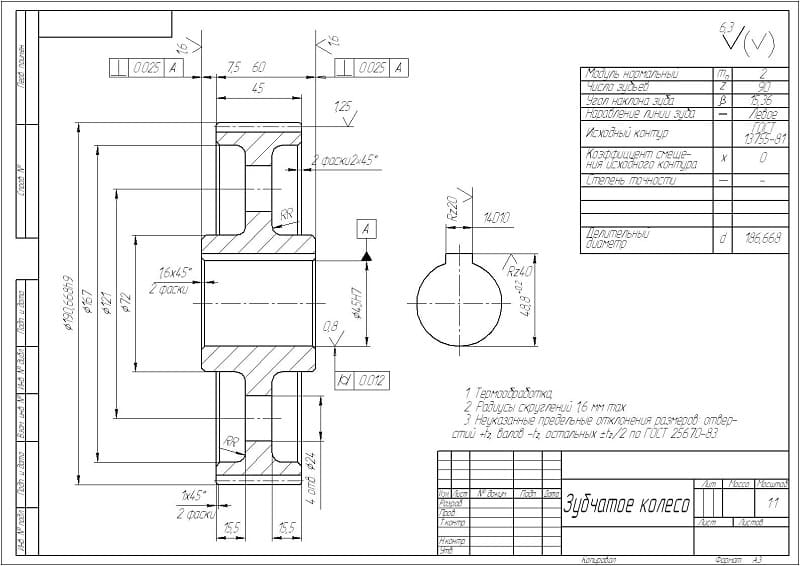
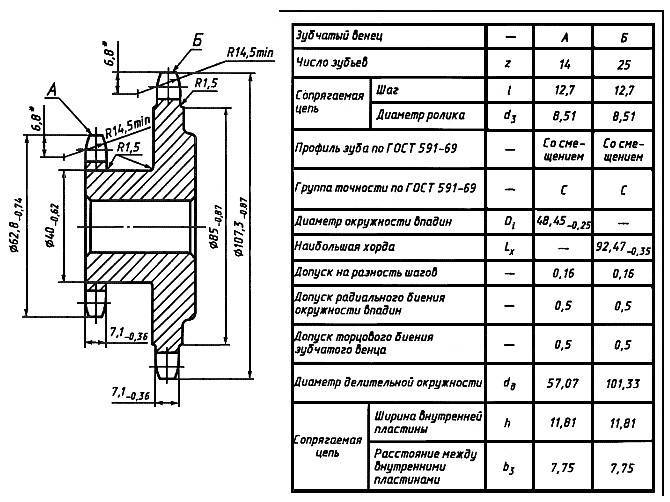
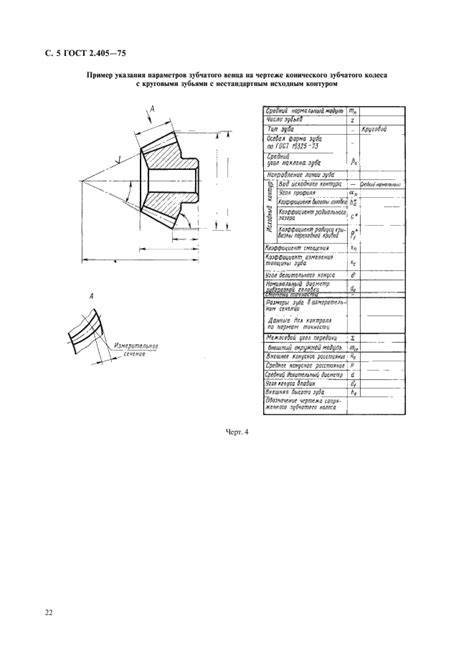
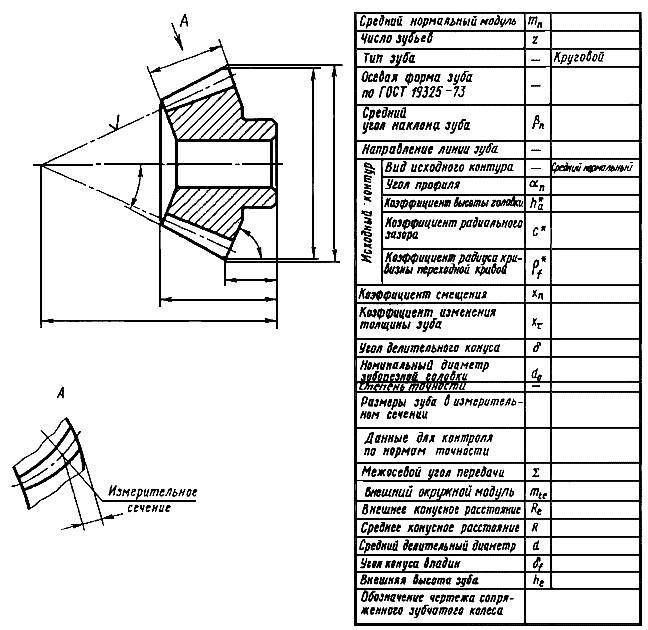
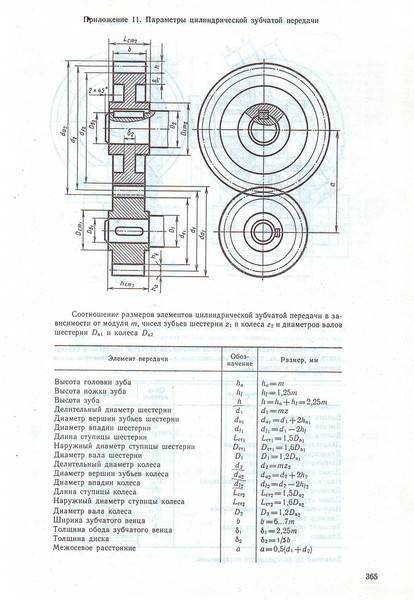
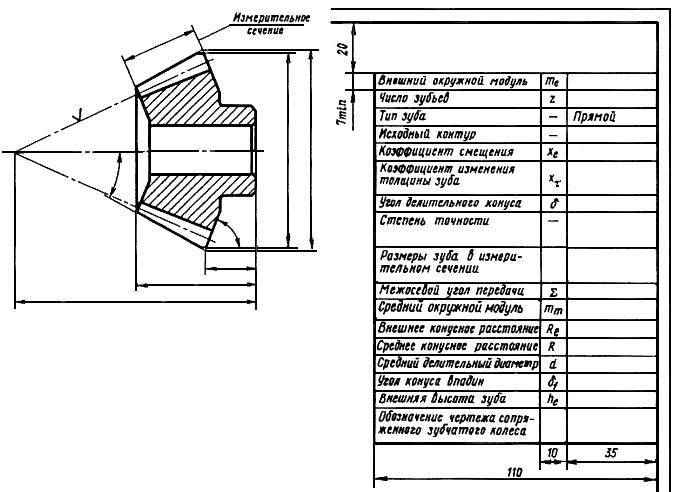
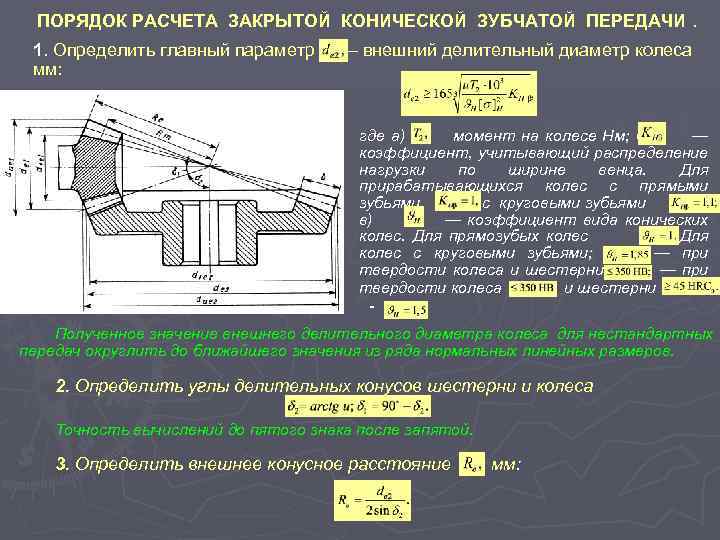
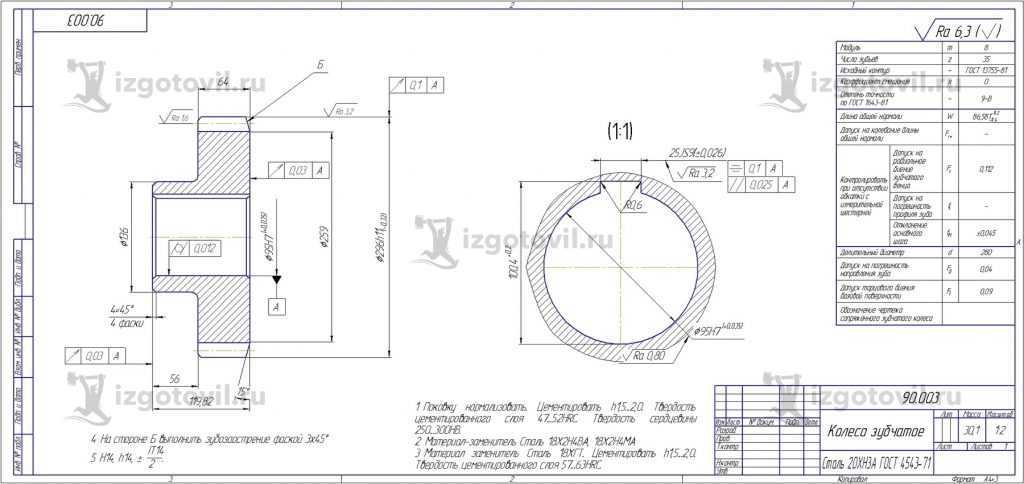
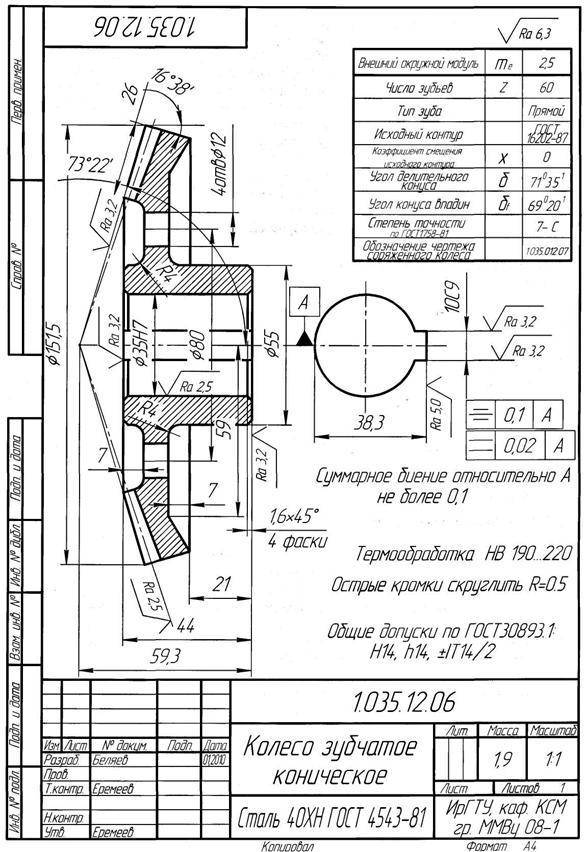
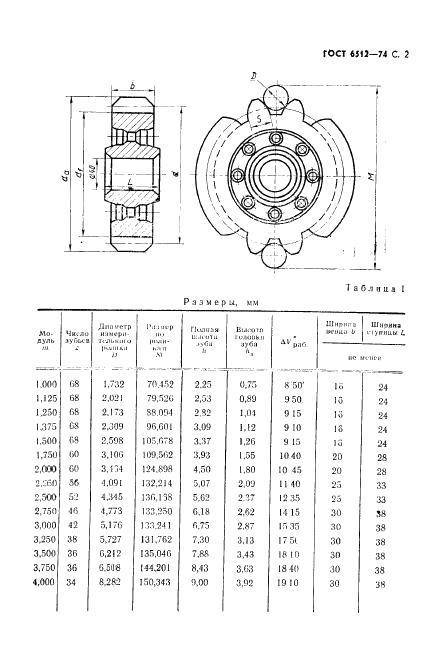
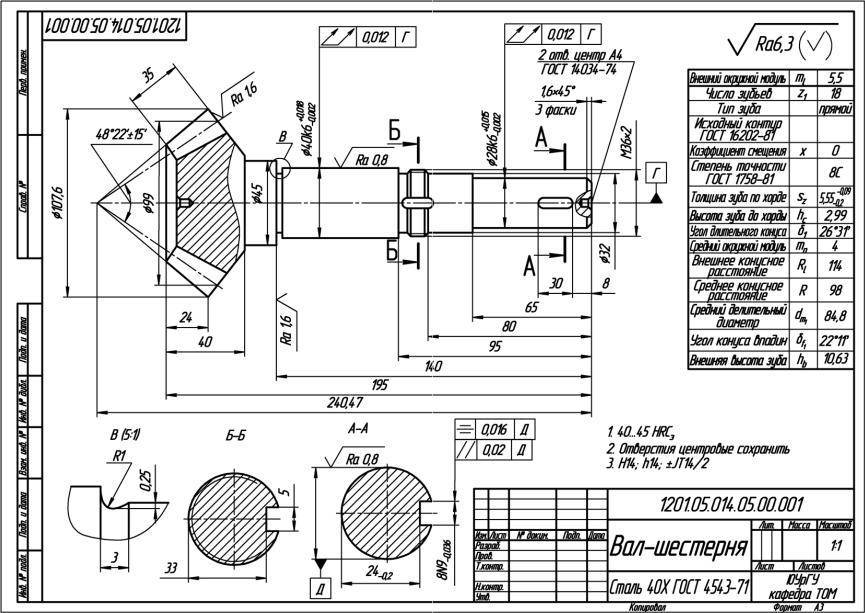
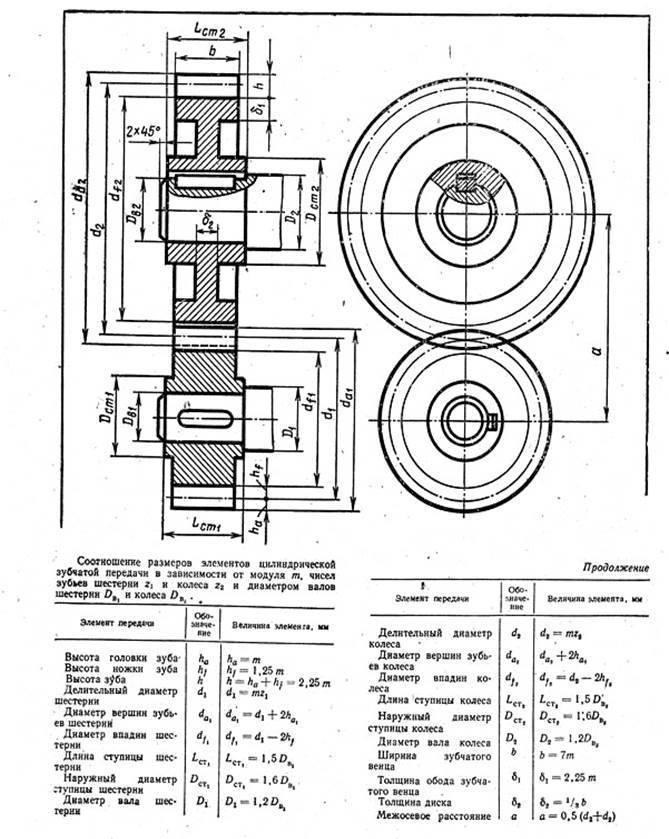
Основные параметры зубчатых цилиндрических передач
Стандарт распространяется на цилиндрические передачи внешнего зацепления для редукторов и ускорителей, в том числе и комбинированных (коническо-цилиндрических, цилиндро-червячных и др.), выполняемых в виде самостоятельных агрегатов. Стандарт не распространяется на передачи редукторов специального назначения и специальной конструкции Для встроенных передач стандарт является рекомендуемым
Межосевые расстояния
| 1 ряд | 40 | 50 | 63 | 80 | 100 | 125 | — | 160 | — | 200 | — | 250 | — | 315 | — | 400 |
| 2 ряд | — | — | — | — | — | — | 140 | — | 180 | — | 225 | — | 280 | — | 355 | — |
| 1 ряд | — | 500 | — | 630 | — | 800 | — | 1000 | — | 1250 | — | 1600 | — | 2000 | — | 2500 |
| 2 ряд | 450 | — | 560 | — | 710 | — | 900 | — | 1120 | — | 1400 | — | 1800 | — | 2240 | — |
1-й ряд следует предпочитать 2-му
Межосевые расстояния для двухступенчатых несоосных редукторов общего назначения
| Быстроходная ступень | 40 | 50 | 63 | 80 | 100 | 125 | 140 | 160 | 180 | 200 | 225 | 250 | 280 | 315 |
| Тихоходная ступень | 63 | 80 | 100 | 125 | 160 | 200 | 225 | 250 | 280 | 315 | 355 | 400 | 450 | 500 |
| Быстроходная ступень | 355 | 400 | 450 | 500 | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 |
| Тихоходная ступень | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 | 1800 | 2000 | 2240 | 2500 |
Коэффициент запаса прочности при работе зуба двумя сторонами
Например: зубья реверсивных передач или зубья сателлитов в планетарных передачах
| Материал колес и термо- обработка | Отливки стальные и чугунные без термо- обработки | Отливки стальные и чугунные с термо- обработкой | Поковки стальные нормали- зованные или улучшенные | Поковки и отливки стальные с поверх- ностной закалкой (сердцевина вязкая) | Стальные, нормали- зованные или улучшенные, а также с поверх- ностной закалкой | Стальные с объемной закалкой | Стальные, подверг- нутые цементации, азоти- рованию, циани- рованию и др. | Чугунные и пласт- массовые колеса |
| Коэфф. | 1,9 | 1,7 | 1,5 | 2,2 | 1,4 — 1,6 | 1,8 | 1,2 | 1 — 1,2 |
Межосевые расстояния для трехступенчатых несоосных редукторов общего назначения
| Быстроходная ступень | 40 | 50 | 63 | 80 | 100 | 125 | 140 | 160 | 180 | 200 |
| Промежуточная ступень | 63 | 80 | 100 | 125 | 160 | 200 | 225 | 250 | 280 | 315 |
| Тихоходная ступень | 100 | 125 | 160 | 200 | 250 | 315 | 355 | 400 | 450 | 500 |
| Быстроходная ступень | 225 | 250 | 280 | 315 | 355 | 400 | 450 | 500 | 560 | 630 |
| Промежуточная ступень | 355 | 400 | 450 | 500 | 560 | 630 | 710 | 800 | 900 | 1000 |
| Тихоходная ступень | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 |
Номинальные передаточные числа
| 1 ряд | 1,0 | — | 1,25 | — | 1,6 | — | 2,0 | — | 2,5 | — | 3,15 | |
| 2 ряд | — | 1,12 | — | 1,4 | — | 1,8 | — | 2,24 | — | 2,8 | — | |
| 1 ряд | — | 4,0 | — | 5,0 | — | 6,3 | — | 8,0 | — | 10 | — | 12,5 |
| 2 ряд | 3,55 | — | 4,5 | — | 5,6 | — | 7,1 | — | 9,0 | — | 11,2 | — |
1-й ряд следует предпочитать 2-му Фактические значения передаточных чисел не должны отличаться от номинальных более чем на 2,5% при номинальном меньше 4,5 и на 4% при номинальном больше 4,5
Коэффициент ширины зубчатых колес (отношение ширины зубчатого колеса к межосевому расстоянию) должен соответствовать: 0,100; 0,125; 0,160; 0,200; 0,315; 0,400; 0,500; 0,630; 0,800; 1,0; 1,25
Численные значения ширины зубчатых колес округляются до ближайшего числа из ряда Ra20 по ГОСТу 6636.
При различной ширине сопряженных зубчатых колес значение коэффициента ширины зубчатых колес относится к более узкому из них.
Формула расчета параметров прямозубой передачи
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.
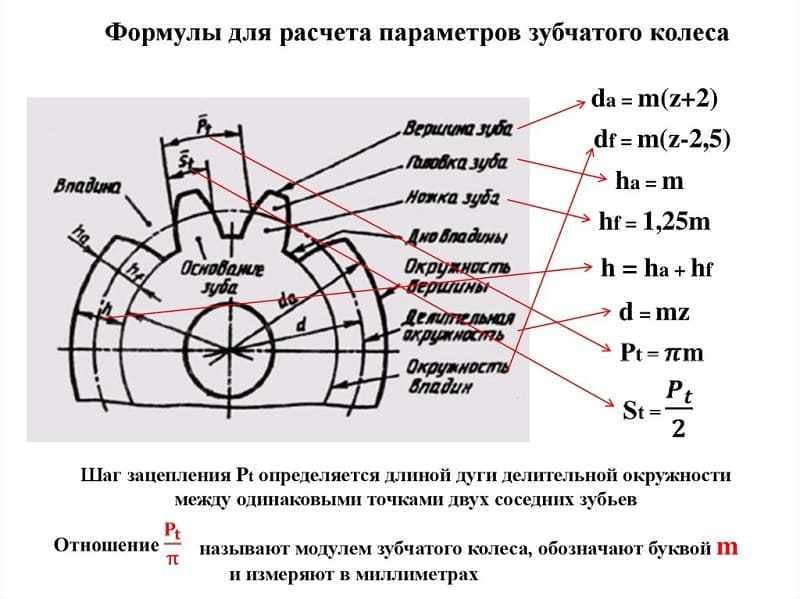
Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:
π×D=t× z,
проведя преобразование, получим:
Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:
выполнив преобразование, находим:
Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов D e получается равным
где h’- высота головки.
Высоту головки приравнивают к m:
Проведя математические преобразования с подстановкой, получим:
De=m×z+2m = m(z+2),
откуда вытекает:
Диаметр окружности впадин D i соответствует D e за вычетом двух высот основания зубца:
где h“- высота ножки зубца.
Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:
Выполнив подстановку в правой части равенства, имеем:
D i = m×z-2×1,25m = m×z-2,5m;
что соответствует формуле:
D i = m(z-2,5m).
Полная высота:
и если выполнить подстановку, то получим:
h = 1m+1,25m=2,25m.
Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.
Следующий важный размер, толщину зубца s принимают приблизительно равной:
- для отлитых зубцов: 1,53m:
- для выполненных путем фрезерования-1,57m, или 0,5×t
Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины s в, получаем формулы для ширины впадины
- для отлитых зубцов: s в =πm-1,53m=1,61m:
- для выполненных путем фрезерования- s в = πm-1,57m = 1,57m
Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:
- усилия, прикладываемые к детали при эксплуатации;
- конфигурация деталей, взаимодействующих с ней.
Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.
Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.
Как рассчитать передаточное число
Шестерня и колесо имеют разное количество зубов с одинаковым модулем и пропорциональный размер диаметров. Передаточное число показывает, сколько оборотов совершит ведущая деталь, чтобы провернуть ведомую на полный круг. Зубчатые передачи имеют жесткое соединение. Передающееся количество оборотов в них не меняется. Это негативно сказывается на работе узла в условиях перегрузок и запыленности. Зубец не может проскользнуть, как ремень по шкиву и ломается.
Расчет без учета сопротивления
В расчете передаточного числа шестерен используют количество зубьев на каждой детали или их радиусы.
Где u12 – передаточное число шестерни и колеса;
Z2 и Z1 – соответственно количество зубьев ведомого колеса и ведущей шестерни.
Применение
Высокие свойства зубчатых передач нашли отражение в широком спектре применений. Во многих промышленных механизмах используются редукторы, призванные понизить число оборотов вращения вала двигателя, для передачи на технологическое оборудование. Помимо изменения скорости, такое устройство также увеличивает механический момент. В итоге маломощный двигатель с большой скоростью вращения, способен приводить в движение медленный и тяжелый механизм.
С целью уменьшения габаритов редуктора его часто выполняют многоступенчатым. Большое количество зубчатых колес входят в последовательное зацепление между собой, обеспечивая высокое передаточное число. Классическим примером подобного устройства являются обычные механические часы. Благодаря множеству специально подобранных передач, скорости движения секундной, минутной и часовой стрелок отличаются друг от друга ровно в 60 раз.
Меняя один комплект на другой, можно получить разные скорости выходного вала. Этот принцип действия лег в основу коробок переключения передач, широко используемых в автомобилестроении, станкостроении и других отраслях.
Обычное зубчатое колесо допускает применение и для повышения скорости выходного вала относительно входного. В общем случае для этого достаточно развернуть редуктор или поменять местами точки подключения двигателя и конечного механизма. Называется подобное устройство мультипликатор. Из особенностей его применения необходимо учитывать запас по мощности двигателя, сопоставимый с передаточным числом механизма.
Зубчатые колеса используются также для изменения направления движения. Две цилиндрические шестерни с одинаковым числом зубьев реализуют функцию смены направления вращения вала. Передачи конической или корончатой конструкции используются в случае необходимости смены положения оси в пространстве. Ведущая и ведомая шестерни в таких механизмах развернуты друг относительно друга на какой-либо угол, значение которого может достигать 90 градусов. При этом передаточное отношение часто равно единице, что обеспечивает одинаковые скорости валов.
Наряду с простыми вариантами передач, содержащих зубчатые колеса, разработаны несколько специальных моделей. С целью снижения материалоемкости, в механизмах с ограниченным углом поворота, используют только часть зубчатого колеса. Такой сектор, обладая всеми основными свойствами зубчатого зацепления, отличается более низкой массой и стоимостью.
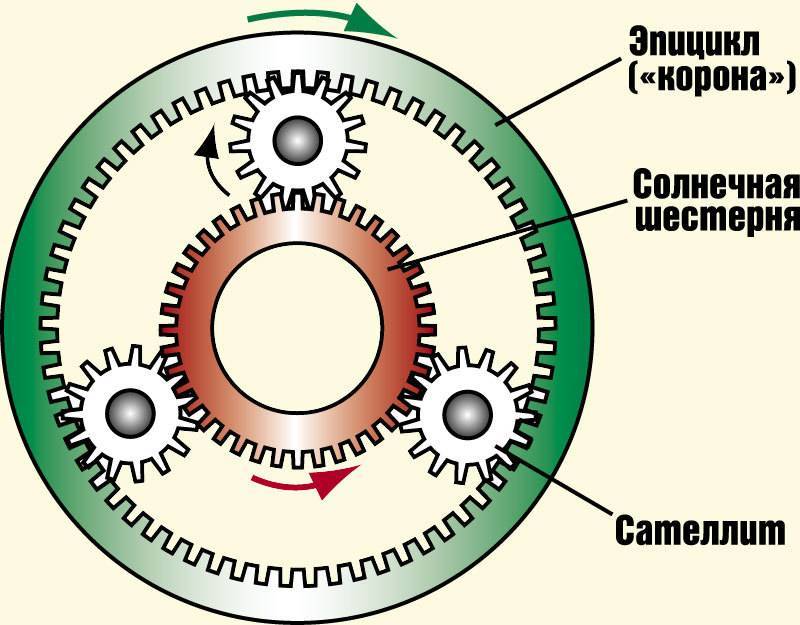
Еще один вариант, называемый планетарной передачей, также характеризуется малым весом и габаритами. При этом устройство обеспечивает высокое значение передаточного числа и пониженный уровень шума в процессе работы. Конструктивно такая передача состоит из нескольких шестерен, имеющих разную степень свободы. За счет этого механизм может не только передавать вращение, но и складывать или выделять угловые скорости разных валов, находящихся на одной оси. Сегодня разработано большое число вариантов планетарных передач, отличающихся типом и взаимным расположением зубчатых колес. Планетарные передачи широко применяются в автомобильной и авиационной технике, тяжелом металлорежущем оборудовании. Среди недостатков, сдерживающих распространение передач данного типа, следует отметить низкий КПД и высокие конструктивные требования к точности изготовления отдельных деталей.
Основные параметры
Для обеспечения подвижности и работоспособности, конструкция отдельных деталей механической передачи должна быть согласована по размерам и геометрии. Для этого при описании подобных устройств принято использовать систему специальных параметров. В их число входят геометрические, массогабаритные и прочностные величины, закрепленные стандартами. Применение стандартных параметров позволяет сравнительно просто производить расчет унифицированных зубчатых передач и обеспечивает гарантированное сопряжение всех изделий между собой. Естественно, что для разных видов, параметры будут несколько отличаться. Далее рассматриваются термины, связанные с конструкцией эвольвентного цилиндрического колеса. Эти параметры, в своем большинстве, описывают основные характеристики и других вариантов колес.
В основе сечения зуба большинства шестерен лежит эвольвентный профиль, который получается на основе одноименной кривой. Его применение легко стандартизируется, характеризуется высокой технологичностью изготовления и низкими требованиями к качеству сборки механизма. Основными параметры эвольвентного зубчатого колеса считаются модуль зацепления и количество зубьев зубчатого колеса. При одном и том же наружном диаметре деталей значения этих величин могут существенно отличаться в разных вариантах конструкции.
Число зубьев определяет коэффициент передачи и геометрические размеры зубьев. На ведущем колесе редуктора оно выполняется меньшим, чем на ведомом. В итоге один нормальный оборот ведущей шестерни приводит к повороту ведомого колеса только на определенный угол. Отношение числа зубьев двух колес дает значение передаточного коэффициента. Размеры зубьев определяются как отношение их количества к длине окружности колеса. С целью упрощения расчетов и гарантированного обеспечения зацепления между разными колесами, предусмотрен дополнительный параметр, называемый модулем зацепления. Любые шестерни с одинаковым модулем обеспечивают взаимодействие между собой и могут использоваться для построения механизмов, без дополнительной обработки.
Сумма ширины зуба и впадины совместно дают шаг зубчатого колеса. Учитывая неравномерность профиля по радиусу и зависимость длины дуги от диаметра, в каждом колесе можно определить бесконечное число значений этого параметра. С целью стандартизации принято рассматривать шаг по делительной окружности, называемый так же окружным шагом. Отношение этого шага к числу пи дает модуль зацепления. В некоторых случаях для описания шестерен используют угловой шаг, измеряемый в градусах. Стандартами предусмотрены и несколько других угловых величин. Например, для упрощения настройки оборудования при изготовлении колес рассматривают угловую ширину зуба и угловую ширину впадины. Определяются они также на основе делительной окружности.
Передаточное число зубчатой передачи
Мы записали уравнения, но как механически поменять местами крутящий момент и скорость? Для этого нужны две шестерни (иногда больше) различных диаметров, чтобы иметь конкретное передаточное число. В любой паре шестерен большее зубчатое колесо будет двигаться более медленно, чем меньшее, но оно будет передавать на выходной вал больший крутящий момент. Таким образом, чем больше величина разницы (или передаточное число) между двумя колесами, тем больше разница их скоростей и передаваемых крутящих моментов.
Передаточное число показывает, во сколько раз зубчатая передача изменяет скорость и вращающий момент. Для него, опять же, имеется очень простое уравнение.
Предположим, что передаточное число равно 3/1. Это будет означать, что вы увеличиваете ваш крутящий момент втрое, а скорость втрое снижаете.
Пример:
Момент входной = 1,5 Н∙м, Скорость входная = 100 об/с,
Передаточное число = 2/3
Момент выходной = Момент входной * 2/3 = 1 Н∙м,
Скорость выходная = Скорость входная * 3/2 = 150 об/с.
Итак, на выходе передачи момент в полтора раза вырос, а скорость точно так же снизилась.
Расчет зубчатого колеса
Он всегда ведется в составе расчета конкретной зубчатой передачи. Исходными данными для него обычно являются мощность (или крутящий момент), угловые скорости (или скорость одного вала и передаточное число), условия работы (характер нагрузки) и срок службы передачи.
Дальнейший порядок относится к закрытой цилиндрической прямозубой передаче.
1. Определение передаточного числа u.
2. Выбор материалов колес в зависимости от условий работы, назначение термообработки и значения твердости рабочих поверхностей зубьев.
3. Расчет зубьев передачи на изгиб.
4. Расчет зубьев передачи на контактную прочность (прочности контактирующих поверхностей зубьев).
5. Определение межосевого расстояния aW из условия контактной прочности и округление его значения до стандартного.
6. Задание модуля из соотношения m = (0,01 — 0,02) х aW и округление его значения до ближайшего стандартного. При этом в силовых передачах желательно иметь m ≥1,5 – 2 мм.
7. Определение суммарного числа зубьев передачи, числа зубьев шестерни и колеса.
8. Выбор коэффициентов формы зубьев для шестерни и колеса.
9. Проверка прочности зубьев по напряжениям изгиба.
10. Проведение геометрического расчета передачи.
11. Определение окружной скорости колеса и назначение соответствующей точности зацепления.
Расчет зубчатого колеса в составе открытой зубчатой передачи несколько отличается от приведенного, но в основном последовательность его такая же.
История
Сама по себе идея механической передачи восходит к идее колеса. Применяя систему из двух колёс разного диаметра, можно не только передавать, но и преобразовывать движение. Если ведомым будет большее колесо, то на выходе мы потеряем в скорости, но зато крутящий момент этой передачи увеличится. Эта передача удобна там, где требуется «усилить движение», например, при подъеме тяжестей. Но сцепление между передаточными колесами с гладким ободом недостаточно жесткое, колёса проскальзывают. Поэтому вместо гладких колес начали использовать зубчатые.
В Древнем Египте для орошения земель уже использовались приводимые в действие быками устройства, состоявшие из деревянной зубчатой передачи и колеса с большим числом ковшей.
Вместо зубьев первоначально использовали деревянные цилиндрические или прямоугольные пальцы, которые устанавливали по краю деревянных ободьев.
Изготовленный в I веке до н.э. Антикитерский механизм состоял из десятков металлических зубчатых колес .
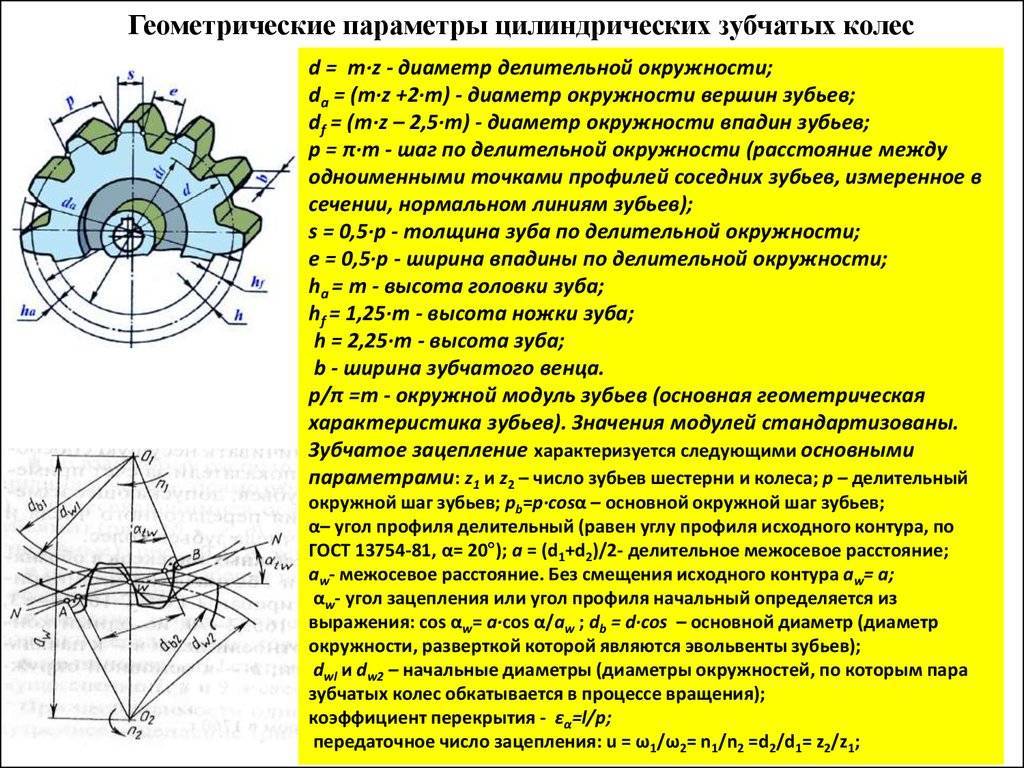
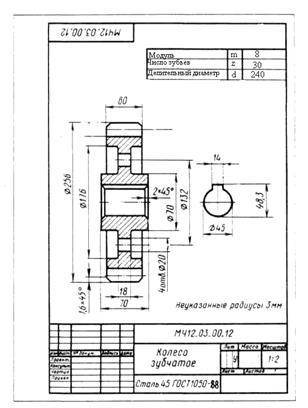
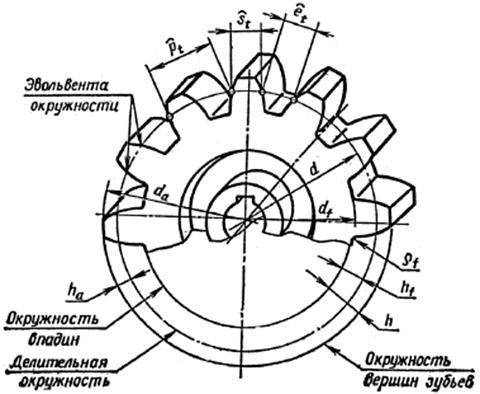
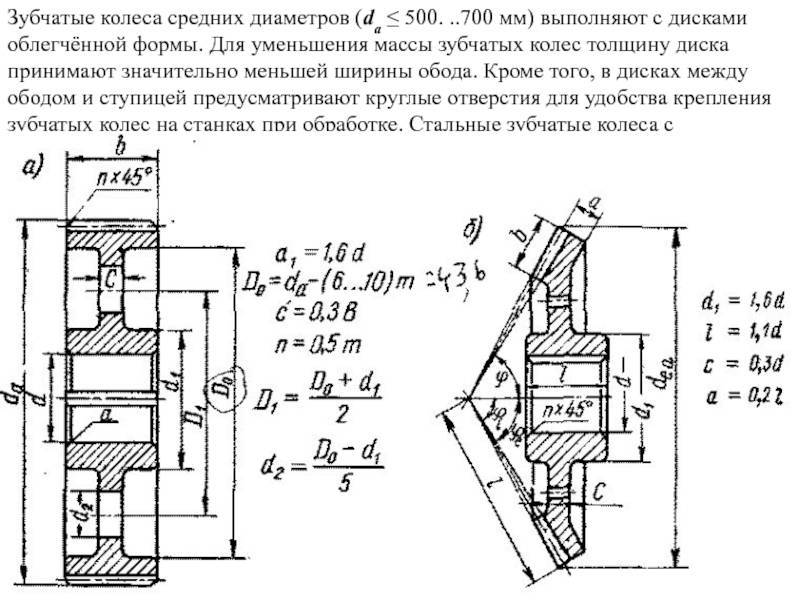
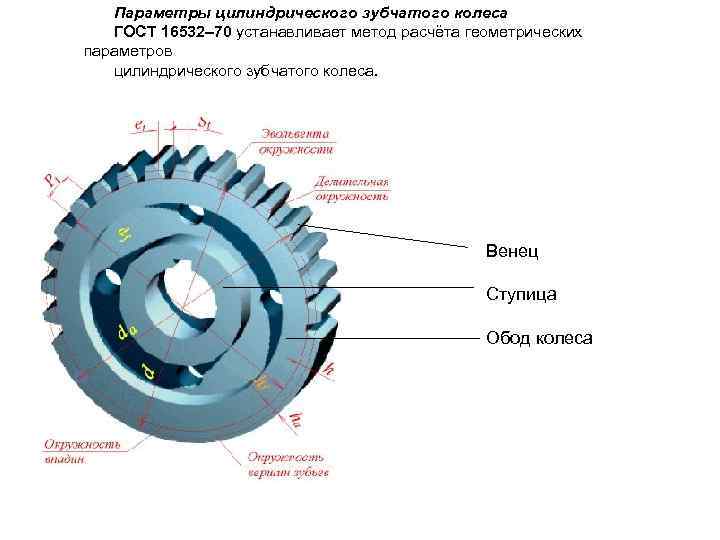
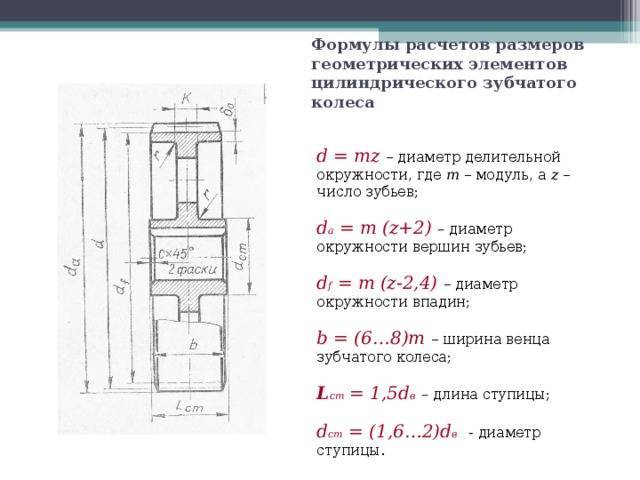
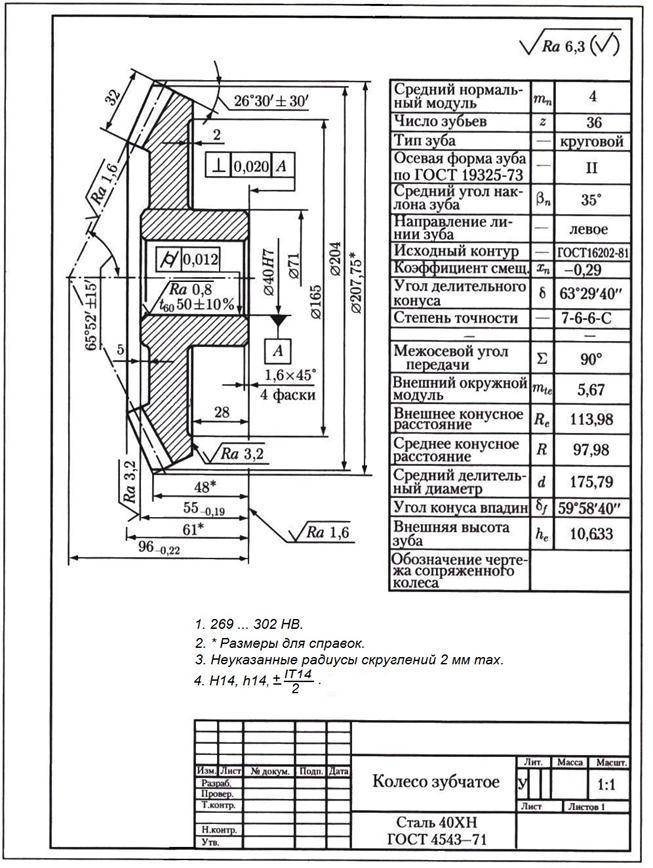
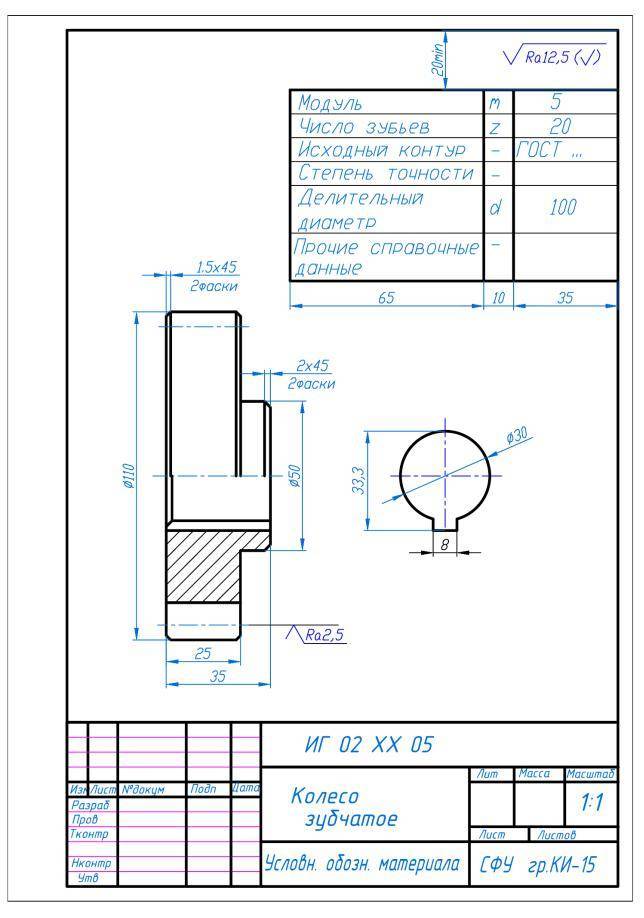
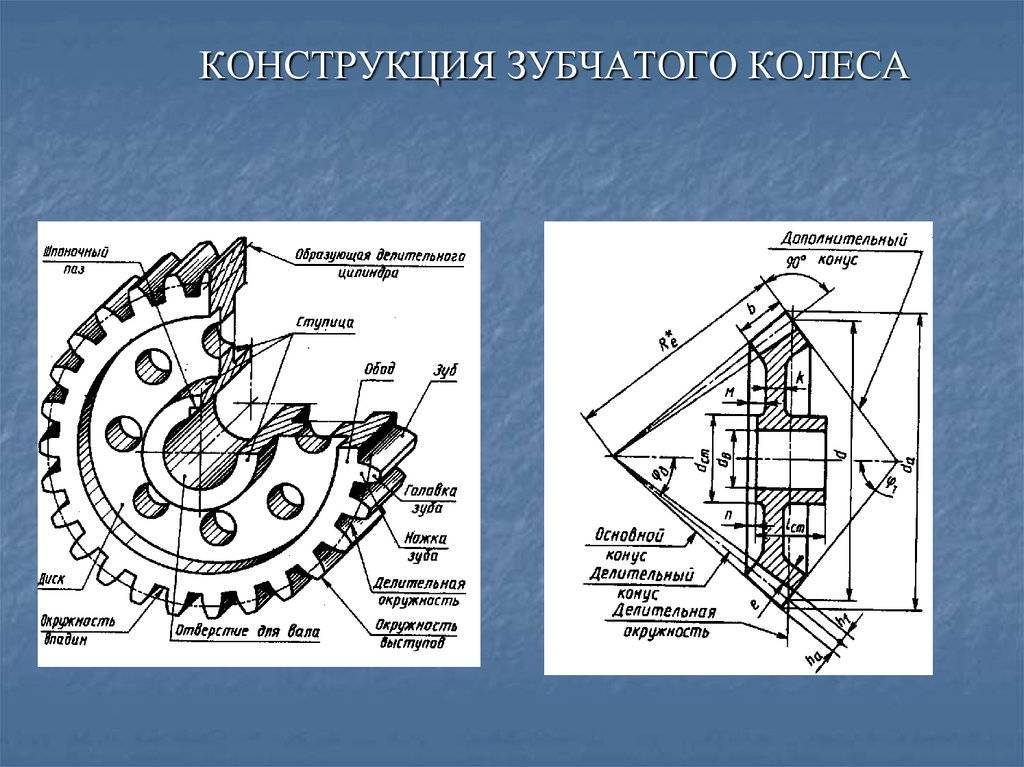
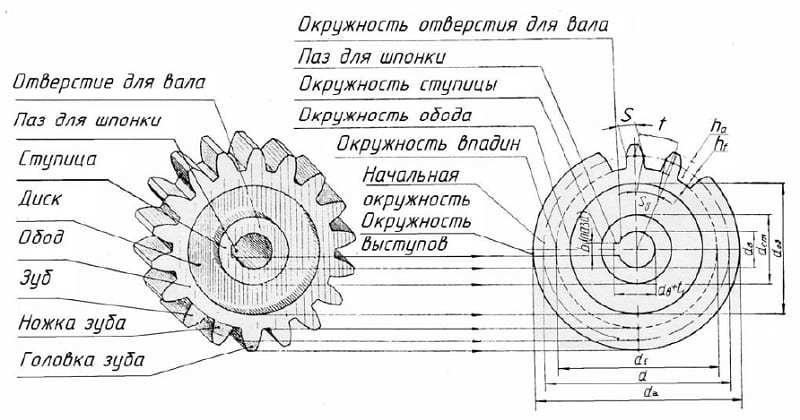
Конструкция и параметры зубчатого колеса
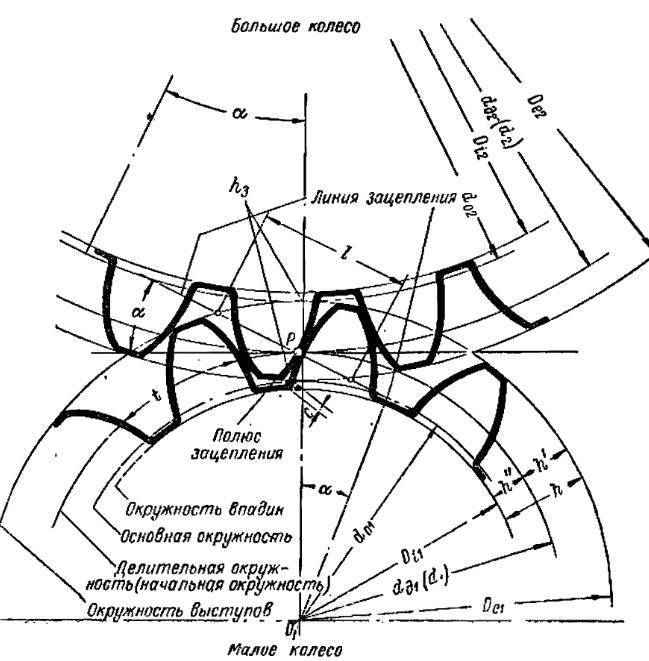
Оно содержит венец с зубьями, диск и ступицу. Имеется три наиболее важных его параметра: модуль, диаметр делительной окружности и количество зубьев. Какую же делительную окружность имеет зубчатое колесо? Чертеж цилиндрического колеса с типовыми эвольвентными зубьями показан ниже.
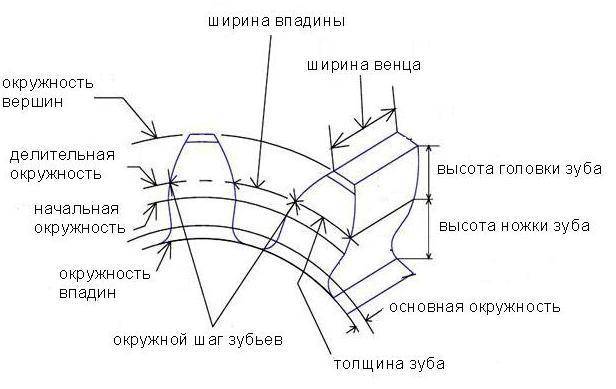
pmd
m = d/z= p/3,14, мм.
Например, зубчатое колесо с 22 зубьями и диаметром 44 мм имеет модуль m = 2 мм. Сцепленные шестерни должны обе иметь один модуль. Значения их стандартизованы, и как раз на делительной окружности модуль данного колеса принимает свое стандартное значение.
Высота головки зуба одного колеса меньше высоты ножки зуба второго, зацепляющегося с ним, благодаря чему образуется радиальный зазор c.
Для обеспечения бокового зазора δ между двумя сцепленными зубьями сумма их толщин принимается меньше их окружного шага p. Радиальный и боковой зазоры предусматриваются для создания необходимых условий смазки, нормальной работы передачи при неизбежных неточностях изготовления и сборки, тепловом увеличении размеров передачи и т. п.
Форма зуба
Зацепления различаются по профилю и типу зубьев. По форме зуба различают эвольвентные, круговые и циклоидальные зацепления. Наиболее часто используемыми являются эвольвентные зацепления. Они имеют технологическое превосходство. Нарезка зубьев может производиться простым реечным инструментом. Эти зацепления характеризуются постоянным передаточным отношением, не зависящим от смещения межцентрового расстояния. Но при больших мощностях проявляются недостатки, связанные с небольшим пятном контакта в двух выпуклых поверхностях зубьев. Это может приводить к поверхностным разрушениям и выкрашиванию материала поверхностей.
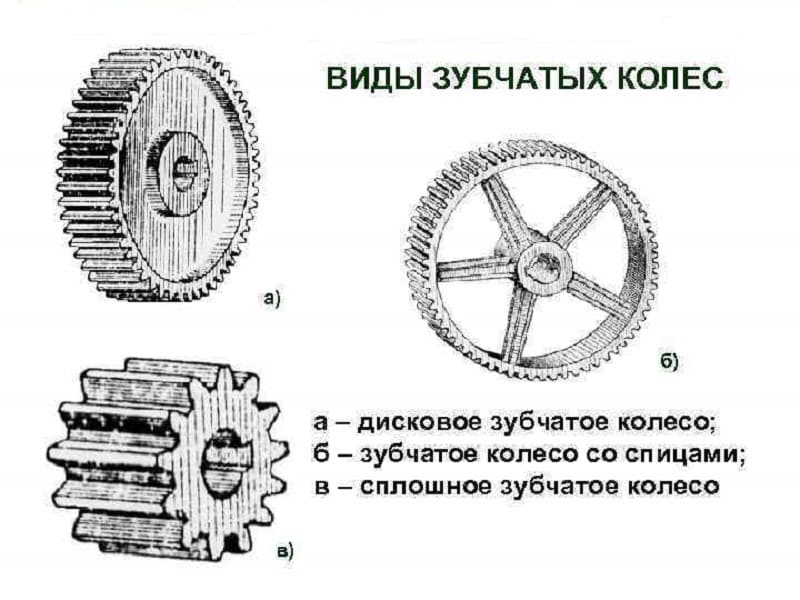
В круговых зацеплениях выпуклые зубья шестерни сцепляются с вогнутыми колесами и пятно контакта значительно увеличивается. Недостатком этих передач является то, что появляется трение в колёсных парах. Виды зубчатых колёс:
- Прямозубые. Это наиболее часто используемый вид колёсных пар. Контактная линия у них параллельна оси вала. Прямозубые колёса сравнительно дешевы, но максимальный передаваемый момент у них меньше, чем у косозубых и шевронных колёс.
- Косозубые. Рекомендуется применять при больших частотах вращения, они обеспечивают более плавный ход и уменьшение шума. Недостатком является повышенная нагрузка на подшипники из-за возникновения осевых усилий.
- Шевронные. Обладают преимуществами косозубых колёсных пар и не нагружают подшипники осевыми силами, так как силы направлены в разные стороны.
- Криволинейные. Применяются при больших передаточных отношениях. Менее шумные и лучше работают на изгиб.
Прямозубые колёсные пары имеют наибольшее распространение. Их легко проектировать, изготавливать и эксплуатировать.
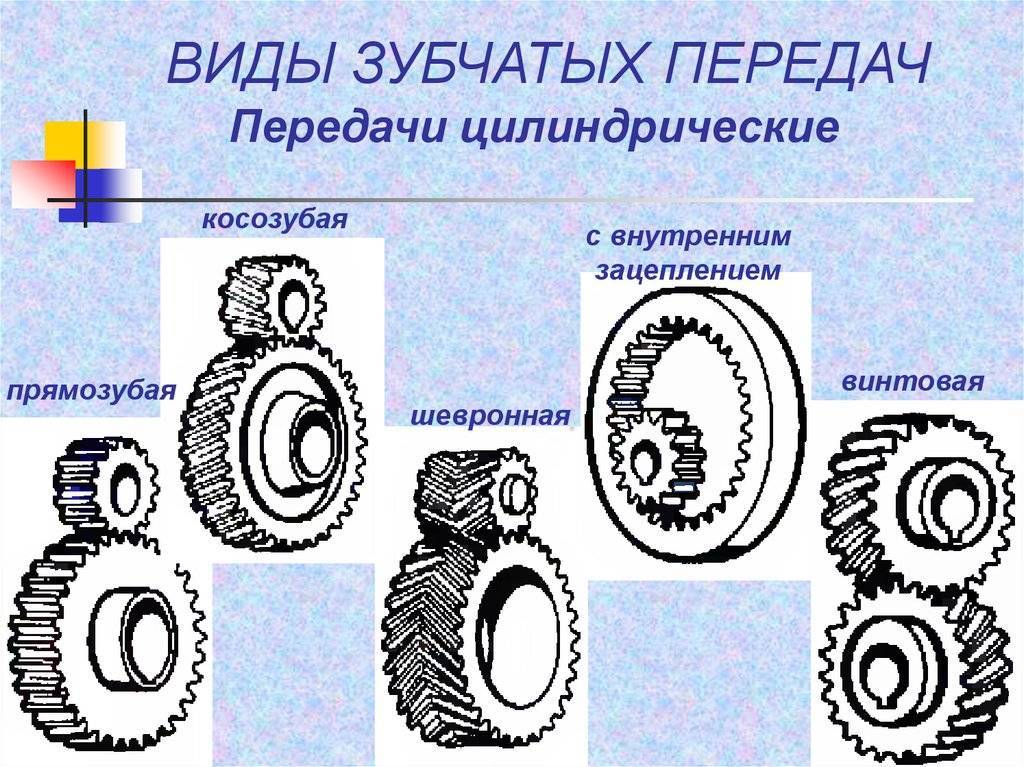
Цилиндрические зубчатые колеса (шестерни):
Цилиндрические зубчатые колеса используются в передачах, где оси валов располагаются параллельно относительно друг друга. При этом они могут располагаться как горизонтально, так и вертикально.
В зависимости от формы продольной линии зуба зубчатые колеса бывают: прямозубые, косозубые и шевронные.

Рис. 1. Цилиндрические зубчатые колеса: прямозубые, косозубые и шевронные
Прямозубое колесо. Этот вид шестерен ввиду своей простой конструкции является наиболее внедряемым в различных системах. В таком виде зубья шестерен располагаются в плоскости, которая перпендикулярна оси вращения. В отличии от косозубых и шевронных колес у данного вида предельный крутящий момент ниже.
Косозубое колесо. Зубья для данного вида колес выполняются под определенным углом к оси вращения шестерен, а по форме образуют часть винтовой линии. По сравнению с прямозубым колесом при работе зубьев данного вида зацепление зубьев происходит плавнее, а за счет увеличенной площади контакта предельный крутящий момент выше. Но для работы колес с косым зубом приходится применять упорные подшипники, так как возникает механическая сила, направленная вдоль оси. В основном косозубые колёса используются там, где нужны передачи большого крутящего момента на высоких скоростях.
Шевронное колесо. Этот вид имеет зубья, которые выполнены в форме буквы V на плоскости вращения колеса. Главной особенностью шевронных колес является то, что силы на осях обеих половин компенсируются, вследствие чего отпадает необходимость в использовании упорных подшипников. Различают шевронное и многошевронное цилиндрическое зубчатое колесо, состоящее соответственно из двух и более полушевронов, а также шевронное цилиндрическое зубчатое колесо со сплошным венцом и разделенными полушевронами.
В отдельные виды выделяются: цилиндрическое колесо с круговыми зубьями, цилиндрическое колесо со смещением (без смещения), циклоидальное, эвольвентное и цевочное цилиндрическое колеса.
Колесо с круговыми зубьями. Передачу с такими колесами называют передачей Новикова. При такой передаче контакт поверхностей зубьев происходит в одной точке на линии зацепления, расположенной параллельно осям колёс. Зубья данного вида колеса выполнены в виде полукруга, радиус которого подбирается под нужные требования. Колеса с круговыми зубьями в сравнении с косозубыми обладают более высокой нагрузочной способностью зацепления, высокой плавностью и бесшумностью работы, но при тех же условиях работы у них снижен КПД и ресурс работы, что не позволяет их применять широко.
Колесо со смещением либо без смещения. Это зубчатое колесо, зубья которого образованы при номинальном положении исходной производящей рейки, характеризуемом отсутствием касания (касанием) делительных поверхностей исходной производящей рейки и обрабатываемого зубчатого колеса.
Циклоидальное колесо. В данном виде профили зубьев шестерни выполнены по циклоидальной кривой. Однако при таком способе зацепления шестерен имеется большой недобор чувствительности из-за изменения расстояния между осями. Циклоидальное колесо применяется в основном в приборостроении. Колесо сложно в изготовлении, поскольку при его создании требуется использование очень многих специальных зуборезных инструментов.
Цевочное колесо. В данном случае зубья одного из колес имеют вид пальцев в форме цилиндра. Такой вид шестерен образовался на базе циклоидального колеса и получил более широкое применение как в машиностроении, так и в приборостроении.
Зубчатые передачи
Зубчатые передачи — это механизм или часть механизма механической передачи, в состав которого входят зубчатые колёса. Зубчатые передачи служат для того, чтобы непрерывно передавать силу и крутящий момент двух валов, расположение которых определяет тип имеющейся зубчатой передачи. Вот о том, что представляют зубчатые передачи, мы и поговорим в этой статье.
Эвольвентное зацепление
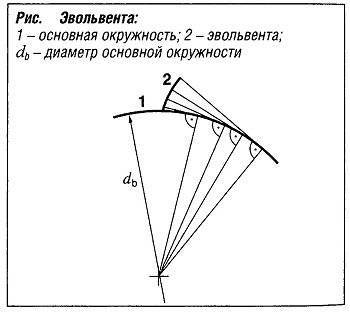
Все прямозубые цилиндрические передачи с одинаковым модулем зацепления могут изготавливаться на одном оборудовании, независимо от количества зубьев и размеров головки.
Модули зацепления цилиндрических и конических зубчатых колес стандартизированы по DIN 780; модули зацепления червячных передач по DIN 780; модули шлицевых соединений по DIN 5480; модули зубчатого зацепления нормального профиля для шестерен со спиральными зубьями по DIN 780.
 |  |
Форма зубьев

Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; червячных передач — DIN 3975; шлицевых соединений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).
Форма зубьев гипоидных передач регламентируется стандартом DIN 867. В дополнение к стандартным углам зацепления (20° для зубчатых передач и 30° для шлицевых соединений) применяются также и углы зацепления 12°, 14°30 15°, 17°30′| 22°30′ и 25°.
Коррегирование зубчатого зацепления
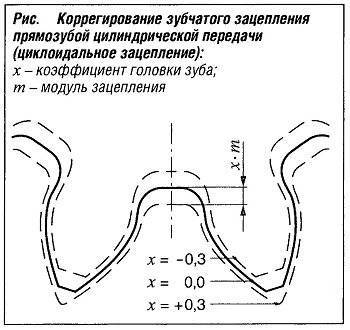
Коррегирование зубчатого зацепления (изменение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подрезания у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.
Зубчатые передачи с точно заданным межосевым расстоянием
У зубчатых пар с точно заданным межосевым расстоянием изменение высоты головки зуба для шестерни и зубчатого колеса производится на одинаковую величину, но в противоположных направлениях, что позволяет сохранить межосевое расстояние неизменным. Такое решение применяется в гипоидных и косозубых передачах.
Зубчатые передачи с изменяемым межосевым расстоянием
Изменение высоты головки зуба для шестерни и зубчатого колеса производится независимо друг от друга, поэтому межосевое расстояние передачи может изменяться. Допускаемые отклонения линейных размеров зубчатых передач регламентированы. Для прямозубых цилиндрических передач — DIN 3960, DIN 58405; для конических передач — DIN 3971; червячных передач — DIN 3975.
Подставляя jη = 0 в приведенные ниже формулы, рассчитывают параметры зацепления без зазора между зубьями. Для определения зазора между зубьями допускаемые отклонения толщины зубьев и зоны их зацепления принимают в соответствии со стандартами DIN 3967 и DIN 58405 в зависимости от требуемой степени точности зубчатой передачи.
Следует отметить, что не обязательно стремиться к нулевому зазору между зубьями. Для компенсации имеющихся отклонений размеров зубьев и сборки шестерен достаточно иметь минимальный зазор, который, кроме того, предотвращает возможность заклинивания зубчатых колес.
Допускаемые отклонения других расчетных параметров (зазор между ножками двух смежных зубьев, межцентровое расстояние) приведены в стандартах DIN 3963, DIN 58405, DIN 3962 Т2, DIN 3967, DIN 3964.
Из чего изготавливаются зубчатые колеса и шестерни

Как правило, в основе зубчатого колеса лежит сталь. При этом шестерня должна иметь большую прочность, так как сами колеса могут иметь разные характеристики по прочности.
По этой причине шестерни изготавливаются из разных материалов, а также такие изделия проходят дополнительную термическую обработку и/или комплексную химическую и температурную обработку.
Например, шестерни, которые выполнены из легированной стали, также проходят процесс упрочнения поверхности, в рамках которого может быть использован метод, позволяющий добиться желаемых характеристик (азотирование, цементация или цианирование). Если для изготовления шестерни используется углеродистая сталь, такой материал проходит поверхностную закалку.
Что касается зубьев, для них предельно важна прочность поверхности, а также сердцевина должна быть мягкой и вязкой. Данные характеристики позволяют избежать излома и быстрого износа рабочей нагруженной поверхности. Еще добавим, что колесные пары механизмов, где нет больших нагрузок и высокой частоты вращения, изготавливают из чугуна. Также можно встретить в качестве материала для изготовления колесных пар бронзу, латунь и даже всевозможные виды пластика.
Сами зубчатые колеса выполняются из заготовки, полученной методом литья или штамповки. Затем применяется метод нарезки зубьев. Нарезка осуществляется путем использования методов копирования, обкатки. Метод обкатки дает возможность изготовить зубья разной конфигурации при помощи одного инструмента (долбяк, червячные фрезы, рейка).
Чтобы осуществить нарезку методом копирования, требуются пальцевые фрезы. После нарезки выполняется термическая обработка. Если же нужно зацепление высокой точности, после такой термообработки дополнительно выполняется шлифовка и обкатка.
Достоинства и недостатки зубчатых передач

Прежде всего, среди достоинств зубчатой передачи можно выделить:
- высокую надежность с учетом расширенного диапазона нагрузок и скоростей;
- компактность, большой ресурс и высокий КПД;
- относительно небольшие нагрузки на валы и подшипники;
- постоянное передаточное число (отношение);
- простота изготовления и обслуживания;
Также выделяют и недостатки зубчатой передачи:
- повышенные требования к качеству изготовления и точности установки;
- при высокой скорости вращения возникает шум по причине возможных неточностей при изготовлении шага и профиля зубьев;
- повышенная жесткость не позволяет эффективно компенсировать динамические нагрузки, в результате чего возникает разрушение и пробуксовки, появляются дефекты;
Напоследок отметим, что во время обслуживания механизм нужно осматривать, производя проверку состояния зубчатых колес, шестерен и зубьев на предмет повреждений, трещин, сколов и т.д.
Также проверяется само зацепление и его качество (часто используется краска, которая наносится на зубья). Нанесение краски позволяет изучить величину пятна контакта, а также расположение относительно высоты зуба. Для регулировки зацепления применяются прокладки, которые ставятся в подшипниковые узлы.
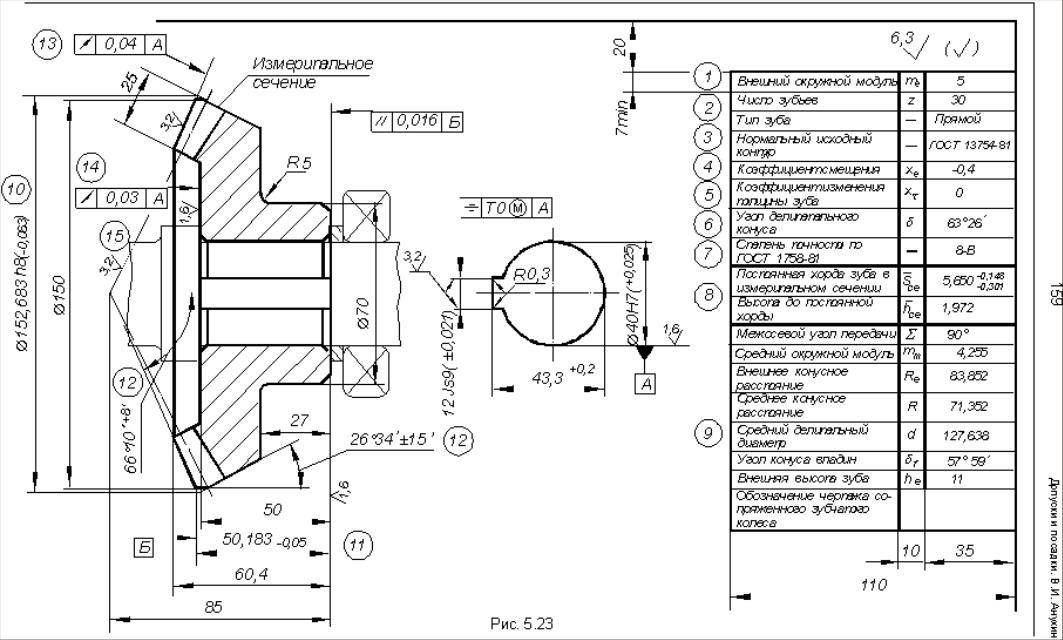
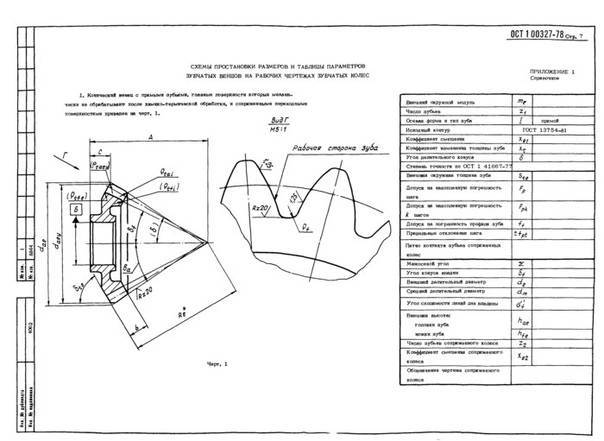
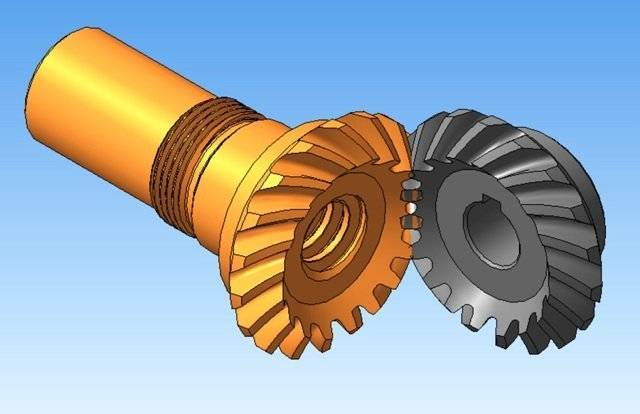
Конические зубчатые колеса (шестерни):
Конические зубчатые колеса используются в передачах, где оси валов пересекаются либо перекрещиваются. Данный тип колес так же широко применяется в машиностроении. Конические зубчатые колеса позволяют решать многие конструкторские задачи, часто встречающиеся в разработке сложных механизмов.

Рис. 2. Конические зубчатые колеса
Различают множество видов конических зубчатых колес.
Колесо с прямыми зубьями. Данная деталь имеет зубья прямой формы, теоретические линии которых проходят через конусную вершину. Данный вид является наиболее простым по технологии изготовления. Прямозубые конические колёса используют при низких окружных скоростях. Передача с такими колесами обеспечивает передаточное отношение до 3.
Колесо с тангенциальными зубьями. Такое колесо имеет прямые зубья, теоретические линии которых расположены касательно к окружности. У данного вида колеса угол спирали различен для различных точек линии зуба. Угол спирали в средней точке зубчатого венца выступает в качестве величины, которая характеризует наклон зубьев.
Колесо с криволинейными зубьями. Такой вид колес имеет ряд преимуществ, среди которых выделяются: мягкий вход, наименьший шум при работе, наибольшая нагрузка и большие окружные скорости. Данный вид передачи встречается среди видов, перечисленных ниже.
Колесо с круговыми зубьями. В данном виде шестерни зубья нарезаны в виде дуги по окружности с определенным углом наклона, который называют углом спирали. Такие шестерни мягко входят в зацепление, вследствие чего издают минимум шума. Они отличаются большей прочностью и допустимостью больших отклонений при установке.
Колесо с нулевым углом наклона зубьев. Такое изделие представляет собой колесо с круговыми зубьями, угол наклона зубьев которого в одной из точек делительной средней линии зуба равняется нулю. Колеса с нулевым наклоном зубьев еще называют «Зерол». Данный вид колес в своей работе дает минимальные осевые нагрузки и широко применяется в передачах с большими скоростями, в том числе в авиастроении, поскольку скорость у них может достигать более 7 метров в секунду. Колеса с нулевым наклоном зубьев могут заменять передачи, в которых были установлены прямозубые шестерни.
Колесо с эвольвентной линией зубьев. В данном типе шестерни при развертке конической основы зубья будут иметь тип эвольвенты основной окружности. Передача зубьев дает непрерывный крутящий переход, который исключает возможность проскальзывания.
Колесо с прямыми зубьями кругового профиля. Данный вид колес имеет профиль зубьев приблизительно круглой формы, у которых поверхность боковин выполнена огибанием рабочей части инструмента, и совершает движение в плоскости по кругу оси инструмента, а также производит поступательное движение мимо зубьев данного типа колеса. Колеса с прямыми зубьями кругового профиля также называют колесом Ривасайкл.
Колесо с круговыми зубьями, образованными сферой. Данное колесо имеет форму зуба, образованную при помощи зацепления на станке поверхностью сферической формы. Колесо также отличается повышенной бесшумностью, плавностью хода и более высокой окружной скоростью.
Плоское колесо. У данного вида колес угол делительного конуса является 90 градусов.
Примечание: Фото https://www.pexels.com, https://pixabay.com
Найти что-нибудь еще?
карта сайта
Коэффициент востребованности
1 367