Зубчатая передача: виды, зацепление, параметры

Применение механизма

Область применения подобных передач целесообразно рассматривать по трём наименованиям: скоростные, силовые, приборные. Все они получили широкое распространение в различных отраслях промышленности. Зубчатые колёса хорошо зарекомендовали себя при создании самых сложных кинематических схем.

Скоростные передачи предназначены для повышения скорости передаваемого вращения. Они успешно применяются в редукторах турбомашин, коробках перемены передач автомобилей (механических и автоматических).

От силовых передач требуется значительное повышение мощности передаваемого вращения. Они эксплуатируются в крановых установках, прокатных станах, тяговых механизмах различного назначения. Такие конструкции работают на малых скоростях. Благодаря этому удаётся передавать большие крутящие моменты. Главным требованием, которое предъявляют к элементам таких систем – плотный контакт между зубьями входящими в зацепление.

На практике распространение получил класс гипоидных агрегатов. Их устанавливают в механизмы и оборудование которые, используются в общем машиностроении. Например, грузовых и легковых автомобилях (в качестве элементов трансмиссии). Особое место такие системы занимают в вертолётостроении. Их применяют на летательных аппаратах практически всех конструкций. Этого удалось добиться благодаря применению зубчатых колёс оснащённых круговыми зубьями. Увеличением угла наклона зуба позволяет передаче работать более плавно. В этом случае удаётся избавиться от рывков и проскальзываний. Наиболее эффективным считается угол т равный 35°. Такие колеса обладают повышенной несущей способностью, надёжностью и долговечностью. Данные передачи работают плавно и практически бесшумно. Они надёжно выполняют свои функции, даже на высоких скоростях. Эта способность реализована благодаря многопарному зацеплению. Такой механизм позволяет снизить динамические нагрузки и предотвратить проскальзывание. Конструкции подобного вида активно применяются в приводе несущих винтов вертолетов различных аэродинамических схем.

Приборные или отсчетные устройства применяют в механизмах научно — исследовательских приборов, счетно-решающих устройствах, бытовой технике. Ведущие и ведомые элементы в этих устройствах могут изготавливаться из цветных металлов или синтетических и полимерных материалов.

В ней должны быть хорошо согласованы углы наклона ведущего и ведомого колеса, точно выверен угол поворота.

Реечная и ременная зубчатая передача

Когда нужно преобразовать вращательное движение в поступательное или наоборот, одно из колес заменяется плоскостью с нарезанными зубьями. Реечная передача отличаются простотой изготовления и монтажа, надежностью и хорошими нагрузочными характеристиками. Применяется в станкостроении и для приводов, где используется поступательное движение: долбежные станки, транспортеры с попеременной подачей.

Зубчато-ременная передача – это гибридная модель, вобравшая положительные качества обеих видов. Отличается постоянством передаточного числа из-за отсутствия проскальзывания. Тихая работа при высоких оборотах и нагрузках достигается путем использования гибких ремней с сердечником. Часто используются в приводах электродвигателей.

На парных шкивах узла агрегата и на эластичном ремне, их связующем, имеются идентичные по профилю зубья. Передача работает не по принципу трения, а используется механизм зацепления. При этом с одной стороны отпадает необходимость сильного натяжения между шкивами и точной регулировки, с другой – смазки между сопрягающимися металлическими деталями.

Расчет параметров

Расчет параметров зубчатых колес выполняют комплексно, для всей передачи. Необходимость расчета отдельного колеса возникает только в процессе ремонта оборудования с неизвестными данными. Расчет начинают с определения требуемого числа зубьев и модуля зацепления. Для того чтобы узнать значение модуля, предварительно проводят расчеты на прочность,  исходя из срока службы и выбранного материала будущего механизма. Также на этом этапе рассчитывают межосевое расстояние между колесами. На основе полученных данных выносливости зубьев вычисляется минимально допустимая величина модуля зацепления. Конкретное его значение выбирается на основе таблиц, приведенных в справочной литературе. Далее, используя требуемое передаточное отношение, производится вычисление числа зубьев на сопрягаемых колесах.

При известном модуле зацепления и количестве зубьев шестерни и колеса, доступно произвести вычисление геометрических размеров отдельных деталей. Основные диаметры и профиль зуба передачи рассчитываются с использованием несложных арифметических действий.  Сложные операции потребуются только для ограниченного числа параметров. Для цилиндрического прямозубого колеса тригонометрические функции содержат только формулы расчета делительного диаметра. При проектировании других типов зубчатых колес, используют тот же математический аппарат, что и для прямозубых, но с добавлением расчетов, учитывающих иную геометрию деталей. Результаты расчетов используют для построения чертежей будущих шестерен, а также при вычислении параметров редукторов.

Заключительным этапом расчета зубчатой передачи становится окончательная проверка механизма на прочность. Если результаты этих вычислений укладываются в принятые нормативы, то полученные значения величин можно использовать для изготовления готового механизма. В противном случае может потребоваться выполнить новый расчет, изменив исходные данные, например, увеличить геометрические размеры, либо поменять тип зубчатой передачи или количество ступеней редуктора.

Форма зуба

Зацепления различаются по профилю и типу зубьев. По форме зуба различают эвольвентные, круговые и циклоидальные зацепления. Наиболее часто используемыми являются эвольвентные зацепления. Они имеют технологическое превосходство. Нарезка зубьев может производиться простым реечным инструментом. Эти зацепления характеризуются постоянным передаточным отношением, не зависящим от смещения межцентрового расстояния. Но при больших мощностях проявляются недостатки, связанные с небольшим пятном контакта в двух выпуклых поверхностях зубьев. Это может приводить к поверхностным разрушениям и выкрашиванию материала поверхностей.

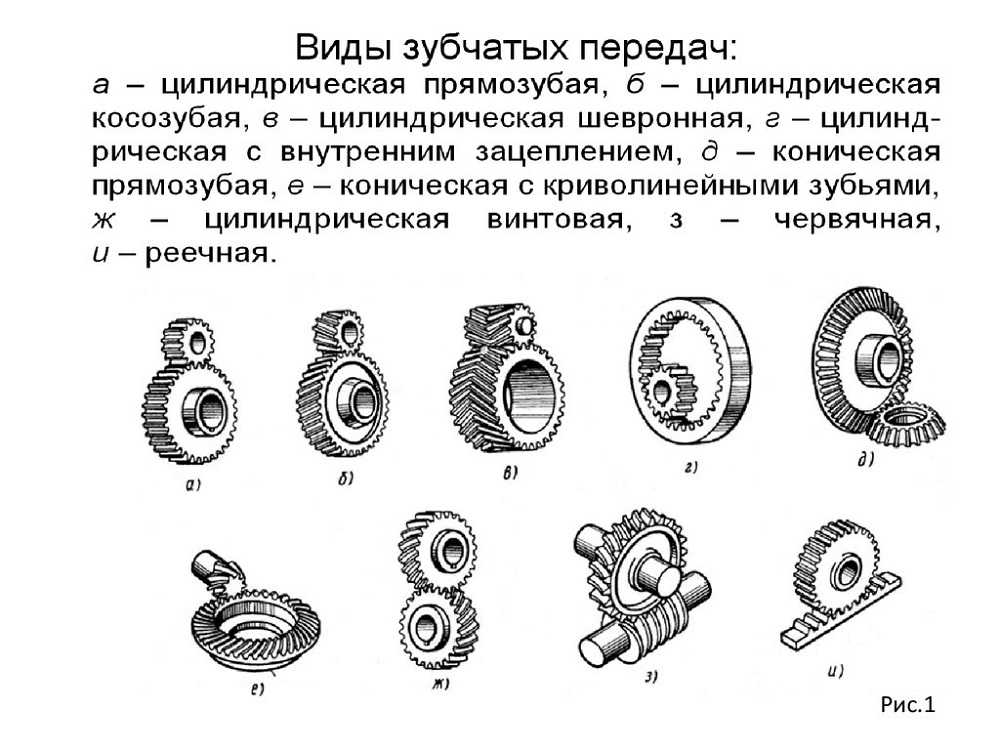
В круговых зацеплениях выпуклые зубья шестерни сцепляются с вогнутыми колесами и пятно контакта значительно увеличивается. Недостатком этих передач является то, что появляется трение в колёсных парах. Виды зубчатых колёс:

1. Прямозубые. Это наиболее часто используемый вид колёсных пар. Контактная линия у них параллельна оси вала. Прямозубые колёса сравнительно дешевы, но максимальный передаваемый момент у них меньше, чем у косозубых и шевронных колёс.
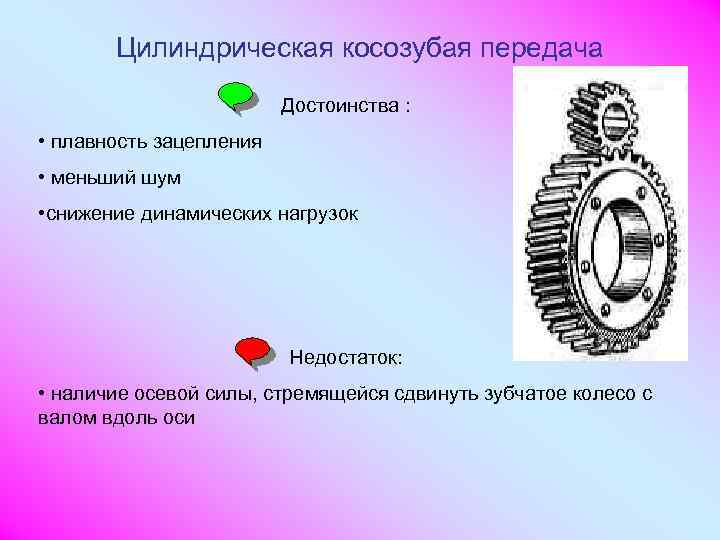
2. Косозубые. Рекомендуется применять при больших частотах вращения, они обеспечивают более плавный ход и уменьшение шума. Недостатком является повышенная нагрузка на подшипники из-за возникновения осевых усилий.
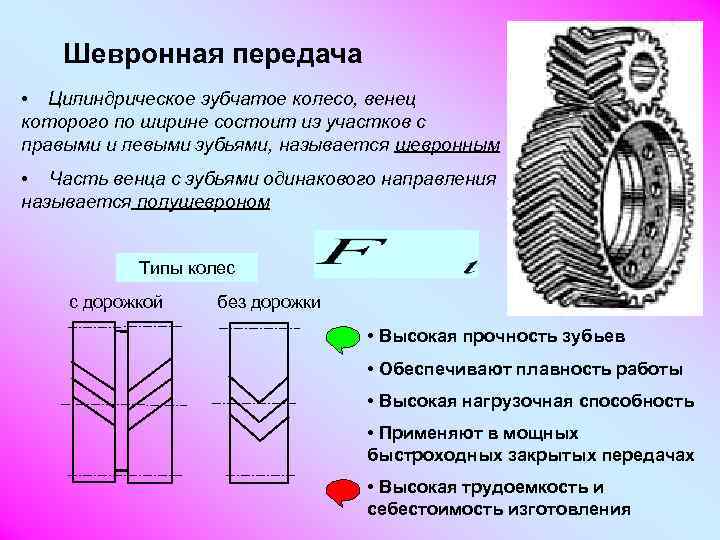
3. Шевронные. Обладают преимуществами косозубых колёсных пар и не нагружают подшипники осевыми силами, так как силы направлены в разные стороны.
4. Криволинейные. Применяются при больших передаточных отношениях. Менее шумные и лучше работают на изгиб.

Прямозубые колёсные пары имеют наибольшее распространение. Их легко проектировать, изготавливать и эксплуатировать.

Размер по роликам зубчатого колеса. Универсальный расчет в Excel.

Приступаем к расчетам, запустив программу MS Excel. Если на вашем компьютере не установлена программа MS Excel, то можно выполнить расчет в программе Calc из свободно распространяемых пакетов Apache OpenOffice или LibreOffice.

Схемы измерений показаны ниже на рисунке. Все замеры выполняются в плоскости торцевого сечения колеса!

Рассмотрим в качестве примера расчет размера по шарикам для косозубого колеса с наружными зубьями.

Исходные данные:

1. Документ, регламентирующий нормальный исходный контур зубьев колеса вписываем

в объединенную ячейку C3D3E3: ГОСТ 13755-82

В примечания к ячейке указаны главные параметры контура

α=20° — угол профиля

ha*=1 – коэффициент высоты головки зуба

c*=0,25 – коэффициент радиального зазора

2. Угол нормального исходного контура α в  градусах, участвующий в дальнейших расчетах, записываем

в ячейку D4: 20

3.  Параметр T, определяющий тип зубьев (наружные или внутренние), вписываем

в ячейку D5: 1

Т=1 — для наружных зубьев

Т=-1 — для внутренних зубьев

4. Модуль зацепления m в  миллиметрах пишем

в ячейку D6: 2,00

5. Число зубьев  z, контролируемого колеса записываем

в ячейку D7: 27

6. Угол наклона зубьев колеса β в градусах пишем

в ячейку D8: 16,1161

7. Коэффициент смещения исходного контура колеса x вводим

в ячейку D9: 0,400

8. Расчетный диаметр измерительных роликов (шариков) D_р в миллиметрах вычисляем

в ячейке D10: =1,7*D6=3,400

D_р=1,7*m

9. Выбираем ближайший к расчетному диаметр шариков D в миллиметрах из имеющихся в наличии и вписываем

в ячейку D11: 3,690

Выбранные шарики, конечно, не должны лежать на дне впадин и должны выступать за наружный диаметр зубьев!

Шарики (ролики) всегда должны соприкасаться с эвольвентой зубьев!

Результаты расчетов:

10. Угол профиля α_tв градусах вычисляем

в ячейке D13: =ATAN (TAN (D4/180*ПИ())/COS (D8/180*ПИ()))/ПИ()*180  =20,7496

α_t=arctg (tg (α)/cos (β))

11. Размер по роликам (шарикам) M в миллиметрах  рассчитываем

в ячейке D14: =ЕСЛИ(ЧЁТН(D7) -D7=0;J3+D5*D11;ЕСЛИ(D8=0;J3*COS ( ПИ()/(2*D7))+D5*D11;J3*((M14^2+(2*K3*COS ((ПИ()/D7+M14)/2))^2) ^0,5)/(2*K3)+D5*D11))=63,000

M=d_D+T*D – для всех колес с четным числом зубьев

M=d_D*cos(π/(2*z))+T*D – для прямозубых колес с нечетным числом зубьев

M=d_D*((λ2+(2*tg(β_D)*cos((πz+λ)/2))2)0,5/(2*tg(β_D))+T*D – для косозубых колес с нечетным числом зубьев

Задача решена! Размер по роликам зубчатого колеса найден! (Точнее – в нашем примере – это размер по шарикам.)

Я умышленно в основную таблицу расчетов не стал включать громоздкие и весьма непростые вспомогательные вычисления, без которых выполнить  этот расчет невозможно. Сейчас мы с ними ознакомимся.

Вспомогательные расчеты:

1. Инволюту угла профиля в точке на концентрической окружности зубчатого колеса, проходящей через центры роликов (шариков)  inv(α_D) вычисляем

в ячейке G3: =TAN (D13/180*ПИ()) -D13/180*ПИ()+D5*(2*D5*D9*TAN (D4/180*ПИ()) -ПИ()/2+D11/(D6*COS (D4/180*ПИ())))/D7=0,042035

inv(α_D)=tg(α_t) -α_t+T*(2*T*x*tg(α) — π/2+D/(m*cos(α)))/z

2. Угол профиля в точке на концентрической окружности зубчатого колеса, проходящей через центры роликов (шариков) α_D в радианах считываем

в ячейке I14: =I13- (TAN (I13) -I13-$G$3)/(1/(COS (I13)^2) -1)  =0,485187891

Для определения α_D решаем уравнение inv(α_D)=tg(α_D) — α_D

Решается это трансцендентное уравнение итерационным методом касательных Ньютона. Подробнее о том, как это делается можно прочитать в статье «Трансцендентные уравнения? «Подбор параметра» в Excel!».

α_D(0)=π/4=3.14/4=0,785398163

n=0…11

α_D(n+1)= α_D(n)— (tg(α_D(n)) -α_D(n)— inv(α_D))/(1/((cos(α_D(n)))2-1))

3. Диаметр концентрической окружности зубчатого колеса, проходящей через центры роликов (шариков)  d_D в миллиметрах рассчитываем

в ячейке J3: =D6*D7*COS (D13/180*ПИ())/(COS (I14)*COS (D8/180* ПИ()))=59,421

d_D=m*z*cos (α_t/(cos (α_D)*cos (β))

4. Параметр  tg(β_D)определяем

в ячейке K3: =COS (D13/180*ПИ())*TAN (D8/180*ПИ()/COS (I14))  =0,307797

tg(β_D)= cos (α_t)*tg (β)/cos (α_D)

5. Значение параметра λ считываем

в ячейке M14: =M13- (SIN (ПИ()/$D$7+M13)*($K$3^2) -M13)/(COS (ПИ()/ $D$7+M13)*($K$3^2) -1)=0,012140062

Для определения λ решаем уравнение sin(π/z+λ)*(tg(β_D))2-λ=0

Решается это трансцендентное уравнение итерационным методом касательных Ньютона – так же, как и уравнение в п.2 этого раздела статьи. (Хотя следует заметить, что есть еще целый ряд методов численного решения подобных уравнений.)

λ₍₀₎=π=3.141592654

n=0…11

λ_(n+1)= λ_(n)— (sin(π/z+λ_(n))*(tg(β_D))2-λ_(n))/(cos(π/z+λ_(n))*(tg(β_D))2-1)

Механизмы

Помимо описанных вариаций, есть еще парочка, которые являются более редкими, но все столь же результативными. В первую очередь, реечная. Используется не для передачи крутящего момента. Напротив, здесь вращательное движение проходит преобразование с помощью рейки. И на выходе мы видим поступательное. Возможен и обратный процесс.

А также существуют винтовые. Они весьма точны и надежны, поэтому реализуются в различных компактных приборах. Но есть и негативная сторона. Проседает эксплуатационный срок, соприкосновение почти без зазоров, а значит, поверхность просто стирается при работе.

Достоинства и недостатки зубчатых передач

Основные достоинства зубчатых передач

по сравнению с другими передачами:

— технологичность, постоянство передаточного числа;

— высокая нагрузочная способность (до N =50000 кВт);

— высокий КПД (до 0,97-0,99 для одной пары колес);

— малые габаритные размеры по сравнению с другими видами передач при равных условиях;

— большая надежность в работе, простота обслуживания;

— сравнительно малые нагрузки на валы и опоры.

К недостаткам зубчатых передач

следует отнести:

— невозможность бесступенчатого изменения передаточного числа;

— высокие требования к точности изготовления и монтажа;

— шум при больших скоростях; плохие амортизирующие свойства;

— громоздкость при больших расстояниях между осями ведущего и ве­домого валов;

— потребность в специальном оборудовании и инструменте для нареза­ния зубьев;

— высокая жесткость, не позволяющая компенсировать динамические нагрузки;

— нерациональное использование зубьев – в работе передачи одновременно участвуют обычно не более двух зубьев каждого из зацепляющихся колёс;

— зубчатая передача не предохраняет машину от возможных опасных перегрузок.

История

Сама по себе идея механической передачи восходит к идее колеса. Применяя систему из двух колёс разного диаметра, можно не только передавать, но и преобразовывать движение. Если ведомым будет большее колесо, то на выходе мы потеряем в скорости, но зато крутящий момент этой передачи увеличится. Эта передача удобна там, где требуется «усилить движение», например, при подъеме тяжестей. Но сцепление между передаточными колесами с гладким ободом недостаточно жесткое, колёса проскальзывают. Поэтому вместо гладких колес начали использовать зубчатые.

В Древнем Египте для орошения земель уже использовались приводимые в действие быками устройства, состоявшие из деревянной зубчатой передачи и колеса с большим числом ковшей.

Вместо зубьев первоначально использовали деревянные цилиндрические или прямоугольные пальцы, которые устанавливали по краю деревянных ободьев.

Изготовленный в I веке до н.э. Антикитерский механизм состоял из десятков металлических зубчатых колес .

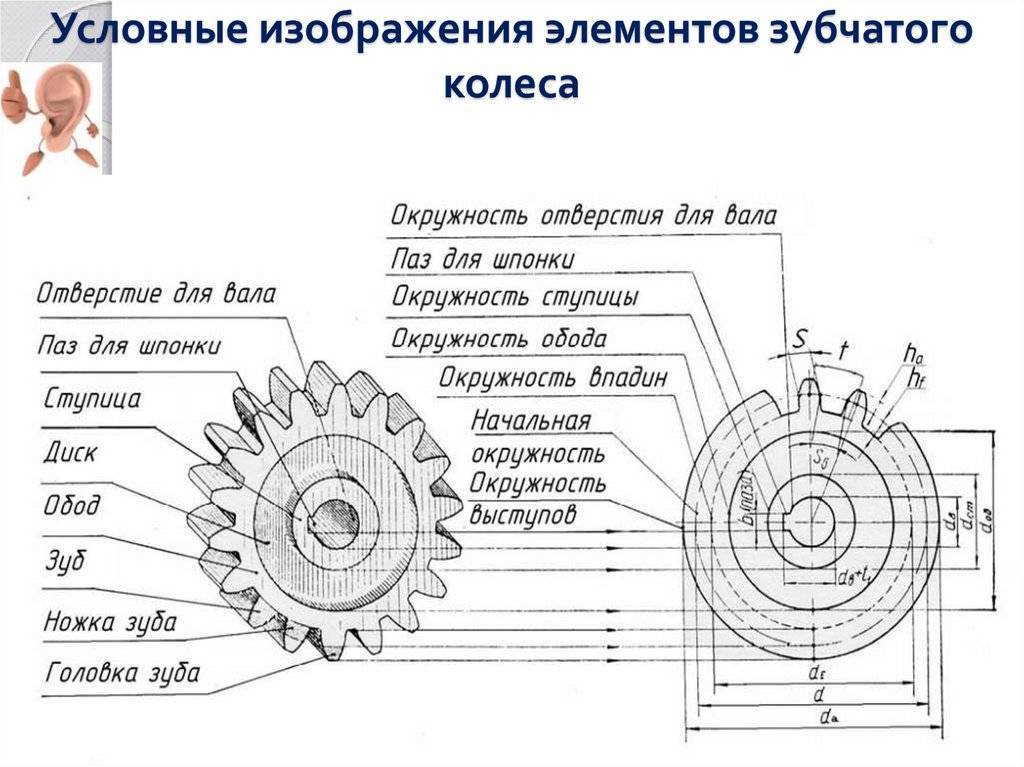
Особенности зубчатого механизма

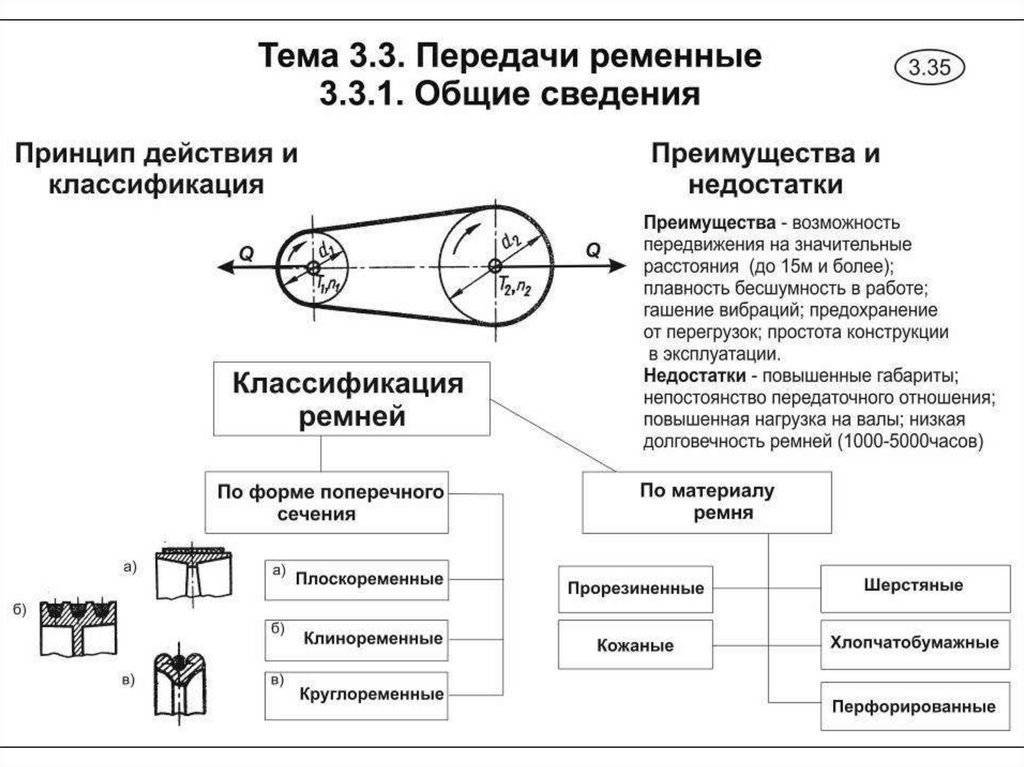
Ременная передача предполагает наличие между шкивами на связанных валах промежуточного звена – гибкого ремня. Зубчатый механизм от такого соединения отличается наличием на поверхности сопряженных деталей зубьев зацепления. По профилю и размеру они идентичны.

Головка зуба колеса входит в зацепление с повторяющей ее профиль впадиной на шестерне. При вращении ведущего вала ведомый проворачивается в противоположную сторону. Между ними конструктивно предусмотрен минимально возможный зазор, обеспечивающий скольжение, тепловое расширение и смазку для недопущения заклинивания. При этом ведущая часть парного механизма называется колесом, а ведомая – шестерней.

У ременной передачи плоскость зацепления ремня со шкивом составляет не менее трети длины окружности. В зубчатом механизме между ведущим колесом и ведомой шестерней под нагрузкой в постоянном контакте находится одна пара зубьев. Колеса и шестерни на валах обычно монтируются на шпоночном соединении.

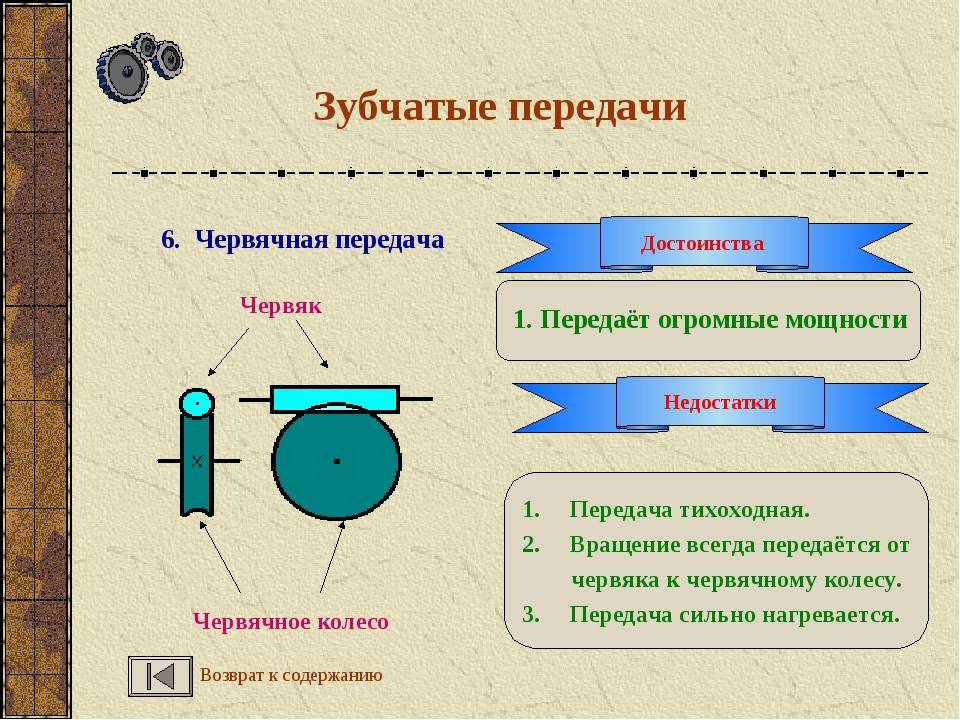
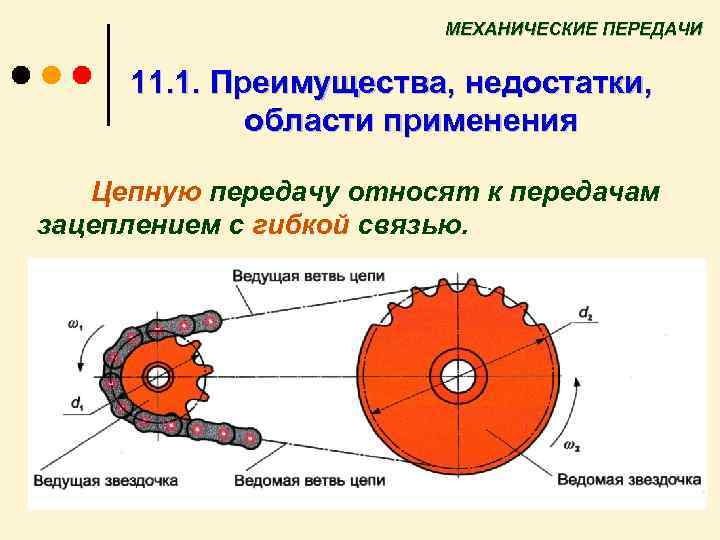
Материал цепей

Все детали цепного механизма должны хорошо сопротивляться повышенным статическим и ударным нагрузкам, и быть достаточно износостойкими. Боковые пластины делают из высокопрочных сплавов, они работают в основном на растяжение. Оси, втулки, ролики, вкладыши и призматические элементы делаются из высокопрочных и хорошо цементируемых сплавов. Цементация проводится на глубину до 1,5 мм и обеспечивает хорошую стойкость к износу трением. После этого детали подвергаются термообработке закаливанием. Твердость доводится до 65 ед.

Зубчатые колеса делают из легированных сталей, также подвергаемых закалке до 60 ед.

Для передач малой скорости и мощности, при умеренных параметрах разгона и торможения применяют ковкие чугуны.

Для снижения шума и повышения плавности хода при ограниченных мощностях используют шестеренки из текстолита или прочных пластмасс. Применяют также наплавку металлических и нанесение полимерных покрытий на детали и узлы, работающие в агрессивных средах.

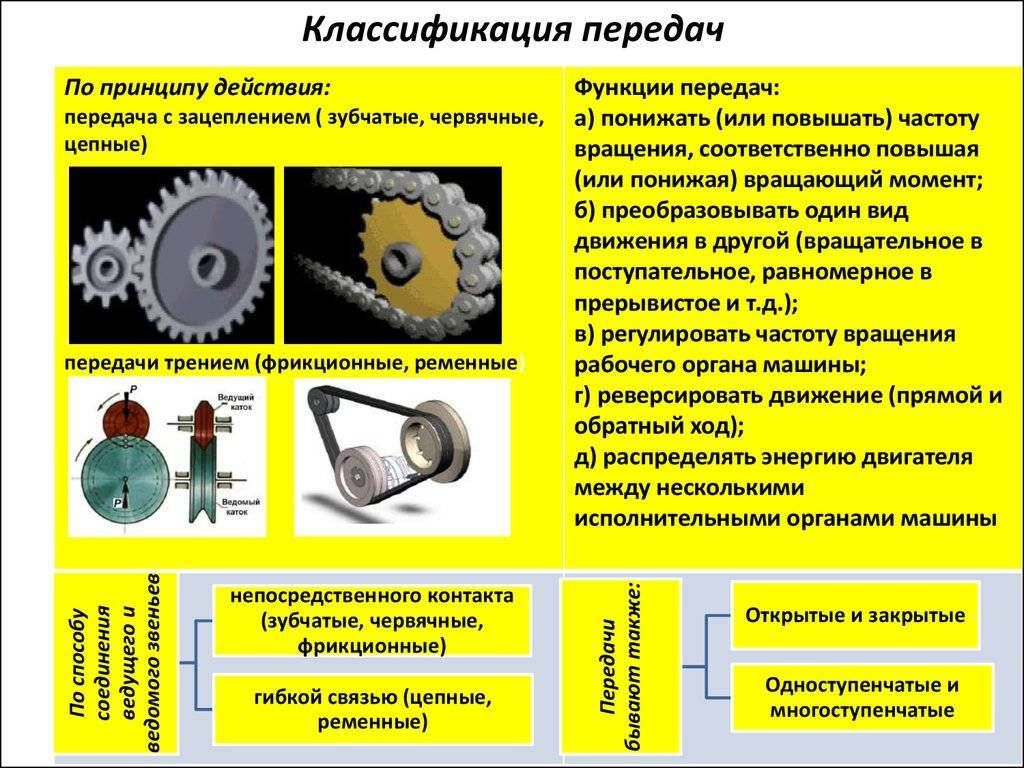
Как классифицируются зубчатые передачи

Сложно выделить единую градацию, на которую бы опирался каждый производитель. Существует значительное количество разнообразных факторов, становящихся фундаментальными в зависимости от задач на производстве. Поэтому и используется несколько вариаций группировки.

Посмотрим, по каким аспектам разделяют эти инструменты на подвиды:

• • Основываясь на расположении осей по сравнению друг с другом. Так появляются параллельные типы, а также пересекающиеся. Отдельной строкой идут перекрещивающиеся. Разумеется, первый вариант – самый простой. И чаще всего выбирается именно он. Но существуют нетипичные задачи, где приходится использовать иные способы. Под осями подразумеваются механизмы, которые крепят колеса.
• • Также некоторые классы опираются на расположение зубьев. Так у нас появляются внутренние и наружные варианты. Эффективность их напрямую опирается на всю систему. Панацеи нет. Им сказать, кто лучше не получится. Используются чаще наружные, но нельзя утверждать, что они результативнее.
• • Корпус тоже имеет значение. Мы уже уточнили, зачем он нужен. Но пока не рассказали, что существуют модели с открытым типом оболочки. И что примечательно, такой вариант работает в принципе без внешней смазки. Сухой ход, как это принято называть. А закрытая модель – ближе к стандарту.
• • Следует внимательно относиться и к размеру. Корректнее – к протяженности окружности. Чем она длиннее, тем больший путь проходит точка при одиночном повороте колеса. Соответственно, выделяют тихоходные и скоростные. Но стоит понимать, что динамика все же зависит от вала. Какой импульс он передаст. А форма лишь подскажет, сможет ли колесо справиться с ним и применить его по назначению.

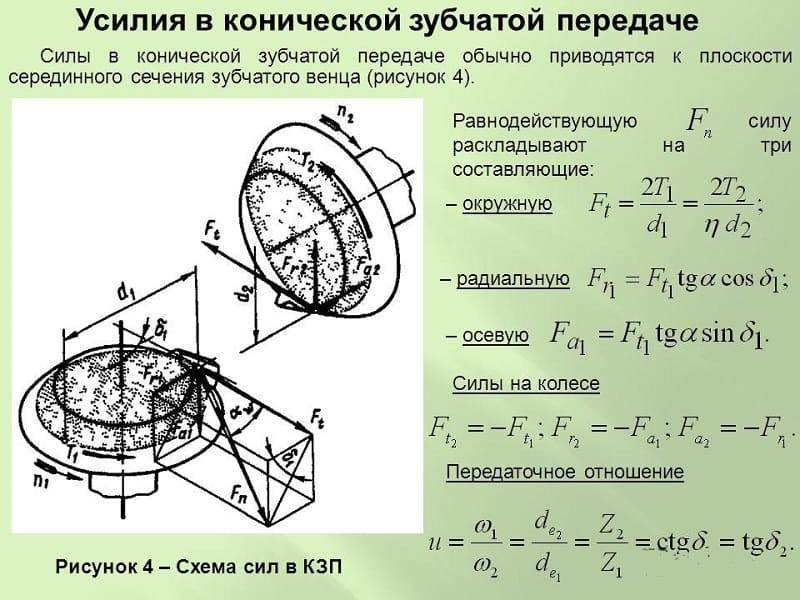
Силы в зацеплении цилиндрической косозубой передачи

— окружная сила;

— вспомогательная окружная сила;

— осевая сила;

— радиальная сила;

— сила нормального

давления.

Наличие в передаче осевой силы приводит к дополнительному нагружению вала изгибающим моментом, а подшипников — осевой силой, что ведет к необходимости применения в опорах радиально-упорных подшипников, воспринимающих радиальную и осевую нагрузку.

Проектные и проверочные расчеты косозубых передач по контактным напряжениям и напряжениям изгиба производят по тем же зависимостям, что и для прямозубых передач. При этом учитывают увеличение прочности зубьев вследствие угла наклона зубьев .

Применение

Высокие свойства зубчатых передач нашли отражение в широком спектре применений. Во многих промышленных механизмах используются редукторы, призванные понизить  число оборотов вращения вала двигателя, для передачи на технологическое оборудование. Помимо изменения скорости, такое устройство также увеличивает механический момент. В итоге маломощный двигатель с большой скоростью вращения, способен приводить в движение медленный и тяжелый механизм.

С целью уменьшения габаритов редуктора его часто выполняют многоступенчатым. Большое количество зубчатых колес входят в последовательное зацепление между собой, обеспечивая высокое передаточное число. Классическим примером подобного устройства являются обычные механические часы. Благодаря множеству специально подобранных передач, скорости движения секундной, минутной и часовой стрелок отличаются друг от друга ровно в 60 раз.

Меняя один комплект на другой, можно получить разные скорости выходного вала. Этот принцип действия лег в основу коробок переключения передач, широко используемых в автомобилестроении, станкостроении и других отраслях.

Обычное зубчатое колесо допускает применение и для повышения скорости выходного вала относительно входного. В общем случае для этого достаточно развернуть редуктор или поменять местами точки подключения двигателя и конечного механизма.  Называется подобное устройство мультипликатор. Из особенностей его применения необходимо учитывать запас по мощности двигателя, сопоставимый с передаточным числом механизма.

Зубчатые колеса используются также  для изменения направления движения. Две цилиндрические шестерни с одинаковым числом зубьев реализуют функцию смены направления вращения вала. Передачи конической или корончатой конструкции используются в случае необходимости смены положения оси в пространстве. Ведущая и ведомая шестерни в таких механизмах развернуты друг относительно друга на какой-либо угол, значение которого может достигать 90 градусов. При этом передаточное отношение часто равно единице, что обеспечивает одинаковые скорости валов.

Наряду с простыми вариантами передач, содержащих зубчатые колеса, разработаны несколько специальных моделей. С целью снижения материалоемкости, в механизмах с ограниченным углом поворота, используют только часть зубчатого колеса. Такой сектор, обладая всеми основными свойствами зубчатого зацепления, отличается более низкой  массой и стоимостью.

Еще один вариант, называемый планетарной передачей, также характеризуется малым весом и габаритами. При этом устройство обеспечивает высокое значение передаточного числа и пониженный уровень шума в процессе работы. Конструктивно такая передача состоит из нескольких шестерен, имеющих разную степень свободы. За счет этого механизм может не только передавать вращение, но и складывать или выделять угловые скорости разных валов, находящихся на одной оси. Сегодня разработано большое число вариантов планетарных передач,  отличающихся типом и взаимным расположением зубчатых колес. Планетарные передачи широко применяются в автомобильной и авиационной технике, тяжелом металлорежущем оборудовании. Среди недостатков, сдерживающих распространение передач данного типа, следует отметить низкий КПД и высокие конструктивные требования к точности изготовления отдельных деталей.

Цилиндрические прямозубые и косозубые передачи

Зубчатые передачи

Общие сведения

В зубчатой передаче движение передается с помощью зацепления пары зубчатых колес. Меньшее зубчатое колесо принято называть шестерней, большее – колесом. Термин зубчатое колесо относиться как к шестерне, так и к колесу. Параметрам шестерни приписывают индекс 1, параметрам колеса – индекс 2. Зубчатые передачи – самый распространенный вид механических передач, так как могут надежно передавать от долей до десятков тысяч киловатт при окружных скоростях до 150 м/с.

— высокая надежность работы в широком диапазоне нагрузок и скоростей;

— сравнительно малые нагрузки на валы и подшипники;

— постоянство передаточного отношения;

— высокие требования к точности изготовления и монтажа;

— шум при больших скоростях.

Классификация зубчатых передач

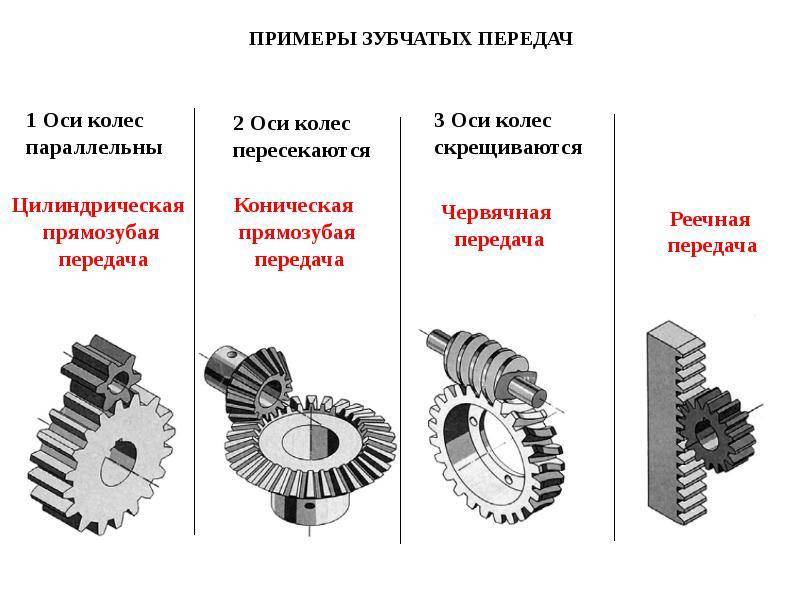
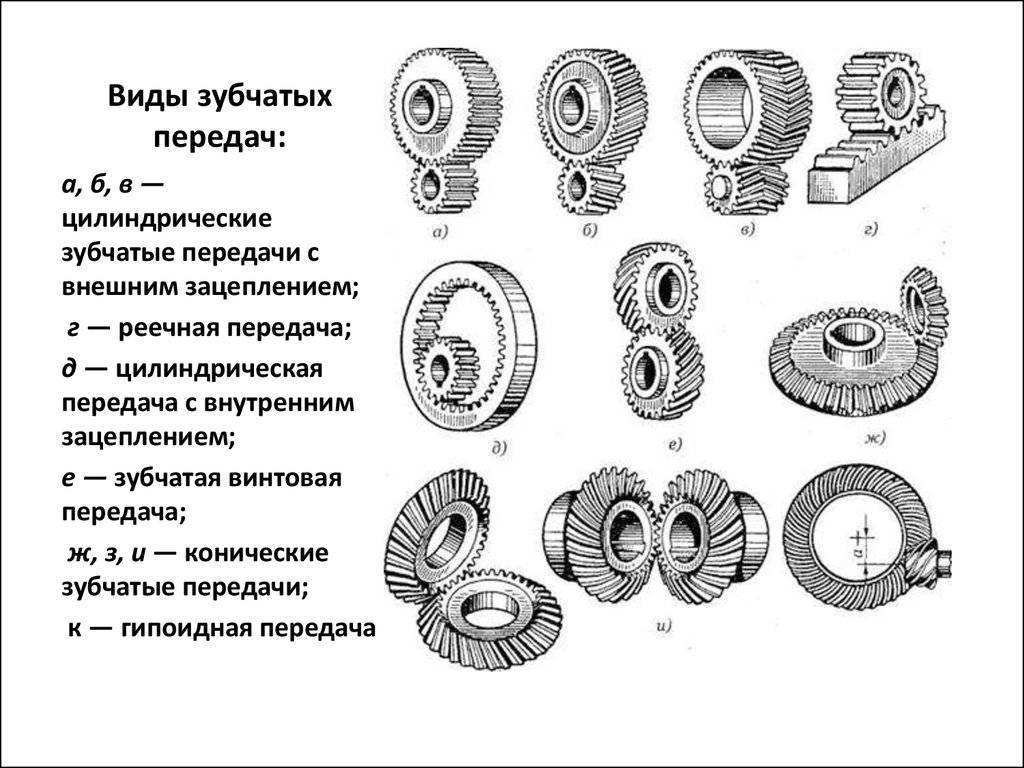
2.1 В зависимости от взаимного расположения геометрических осей валов зубчатые передачи бывают:

— цилиндрические – при параллельных осях в соответствии с рисунком 1.1;

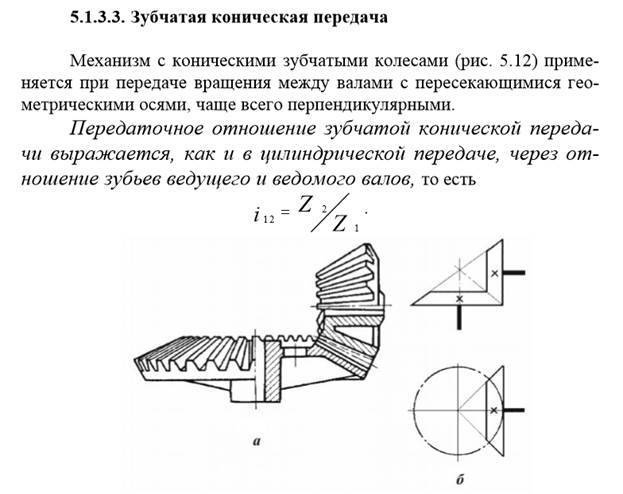
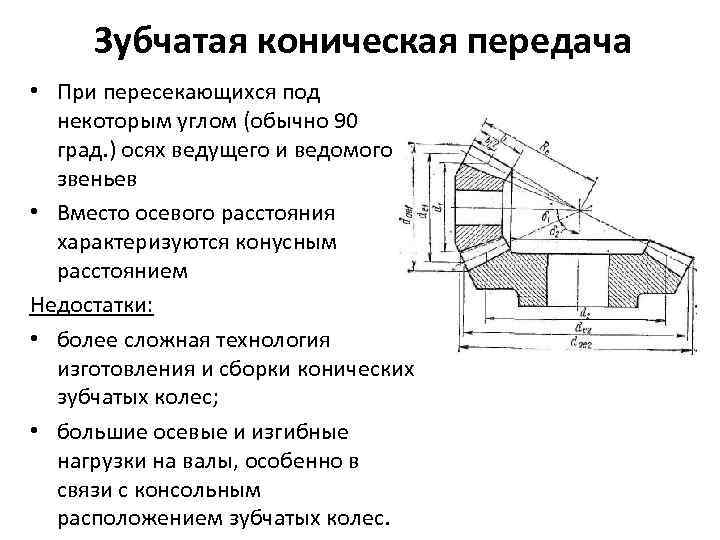
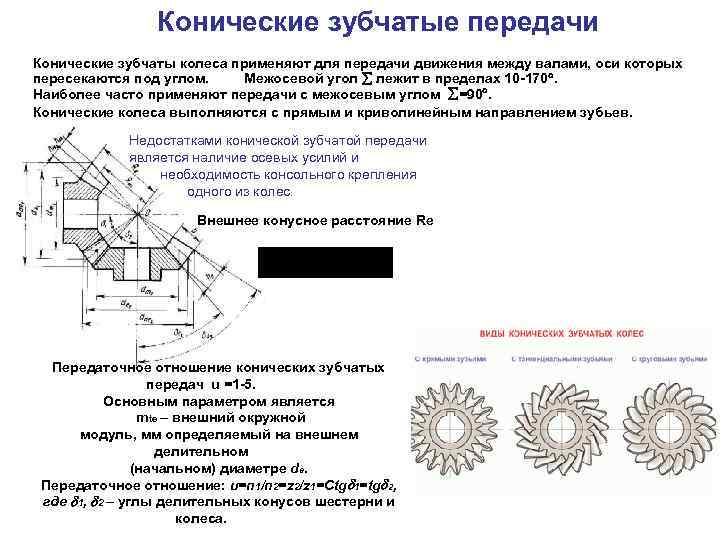
— конические – при пересекающихся осях в соответствии с рисунком 1.2;

— винтовые – при скрещивающихся осях в соответствии с рисунком 1.3.

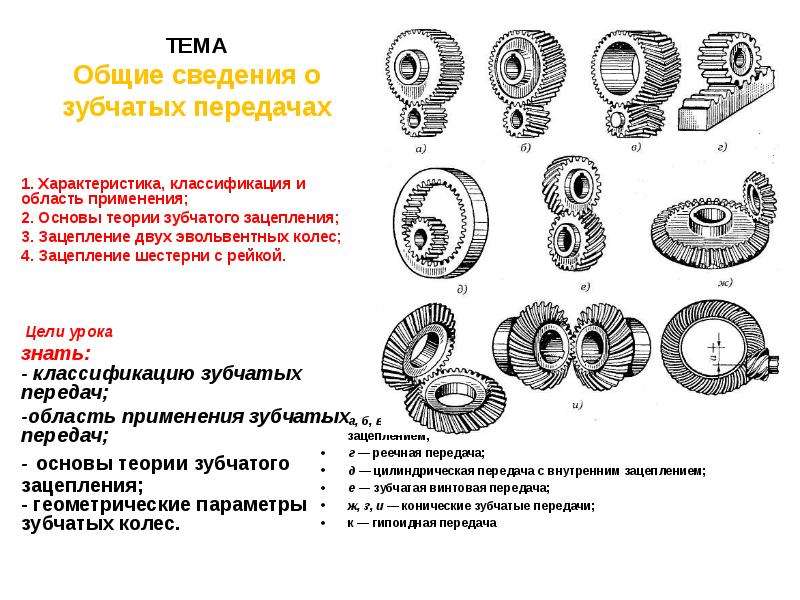
2.2 В зависимости от расположения зубьев на ободе колес различают передачи: прямозубые, косозубые, шевронные и с круговыми зубьями в соответствии с рисунком 1.1.

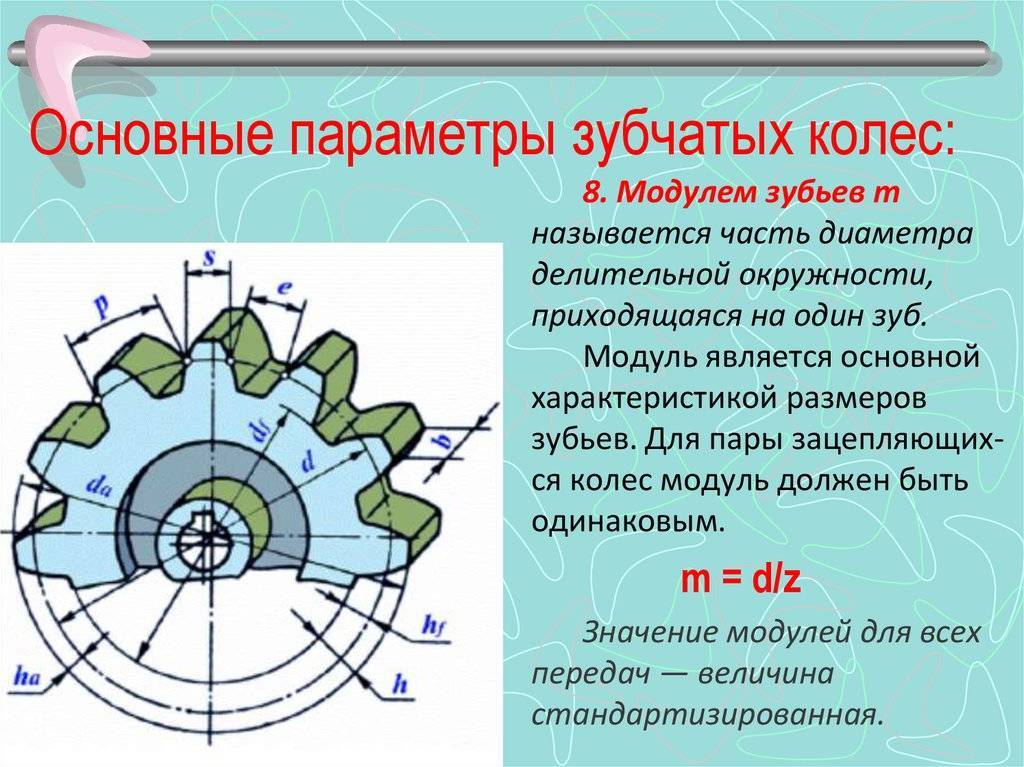
Основные параметры

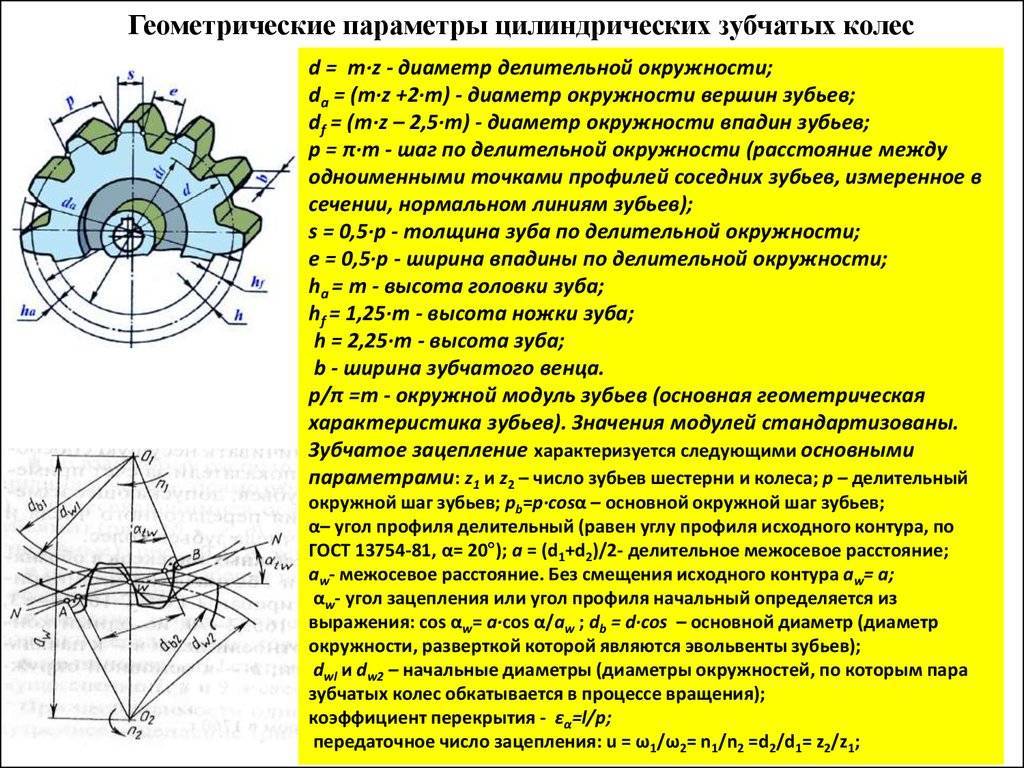
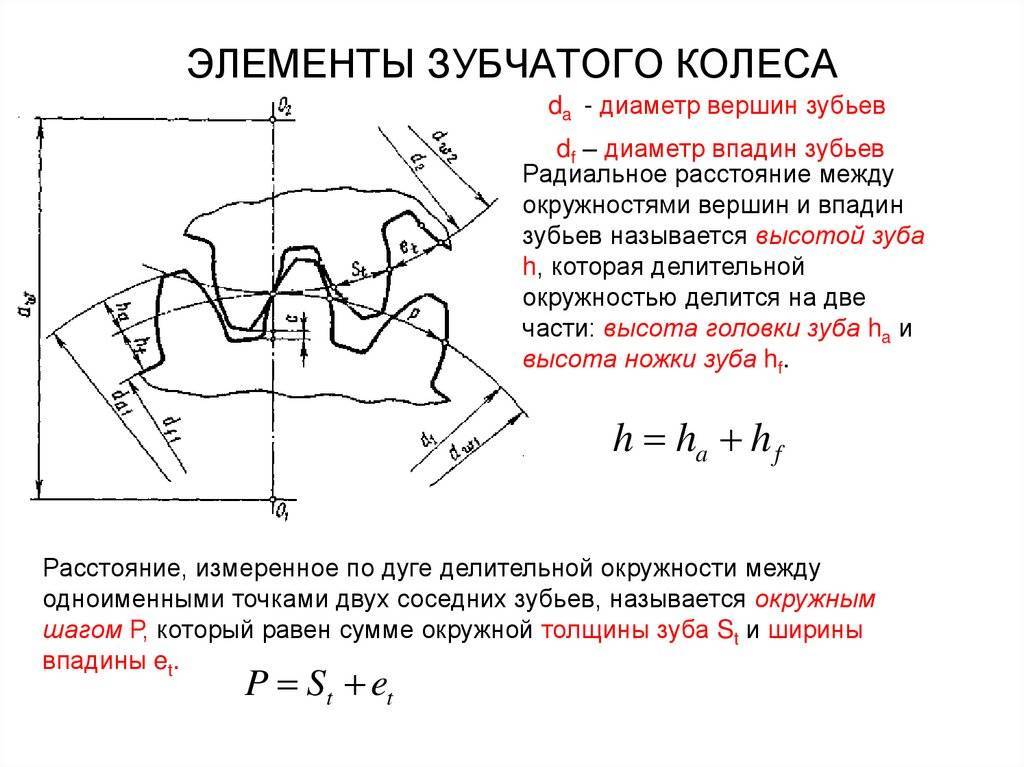
Для обеспечения подвижности и работоспособности, конструкция отдельных деталей механической передачи должна быть согласована по размерам и геометрии. Для этого при описании подобных устройств принято использовать систему специальных параметров. В их число входят геометрические, массогабаритные и прочностные величины, закрепленные стандартами. Применение стандартных параметров позволяет сравнительно просто производить расчет унифицированных зубчатых передач и обеспечивает гарантированное сопряжение всех изделий между собой. Естественно, что для разных видов, параметры будут несколько отличаться. Далее рассматриваются термины, связанные с конструкцией эвольвентного цилиндрического колеса. Эти параметры, в своем большинстве, описывают основные характеристики и других вариантов колес.

В основе сечения зуба большинства шестерен лежит эвольвентный профиль, который  получается на основе одноименной кривой. Его применение легко стандартизируется,  характеризуется высокой технологичностью изготовления и низкими требованиями к качеству сборки механизма. Основными параметры эвольвентного зубчатого колеса  считаются модуль зацепления и количество зубьев зубчатого колеса. При одном и том же наружном диаметре деталей значения этих величин могут существенно отличаться в разных вариантах конструкции.

Число зубьев определяет коэффициент передачи и геометрические размеры зубьев. На ведущем колесе редуктора оно выполняется меньшим, чем на ведомом. В итоге один нормальный оборот ведущей шестерни приводит к повороту ведомого колеса только на определенный угол. Отношение числа зубьев двух колес  дает значение передаточного коэффициента. Размеры зубьев определяются как отношение их количества к длине окружности колеса. С целью упрощения расчетов и гарантированного обеспечения зацепления между разными колесами, предусмотрен дополнительный параметр, называемый модулем зацепления. Любые шестерни с одинаковым модулем обеспечивают взаимодействие между собой и могут использоваться для построения механизмов, без дополнительной обработки.

Сумма ширины зуба и впадины совместно дают шаг зубчатого колеса. Учитывая неравномерность профиля по радиусу и зависимость длины дуги от диаметра, в каждом колесе можно определить бесконечное число значений этого параметра. С целью стандартизации принято рассматривать шаг по делительной окружности, называемый так же окружным шагом. Отношение этого шага к числу пи дает модуль зацепления. В некоторых случаях для описания шестерен используют угловой шаг,  измеряемый в градусах. Стандартами предусмотрены и несколько других угловых величин. Например, для упрощения настройки оборудования при изготовлении колес рассматривают угловую ширину зуба и угловую ширину впадины. Определяются они также на основе делительной окружности.

Основные виды зубчатых передач

В различных областях промышленности и приборостроения активно применяются все разновидности зубчатых передач. Ежегодно подобные механизмы производятся миллионными партиями. Сфера их использования настолько обширна, что найти прибор, в работе которого применяется вращательное движение без помощи зубчатых соединений, достаточно проблематично.

По конструктивному исполнению зубчатые передачи подразделяются на следующие категории:

• Цилиндирическая. Используется наиболее часто, так как имеет более простую относительно других типов технологию производства шестерен. Цилиндрическая зубчатая передача применяется для передачи крутящего момента между валами, которые находятся в параллельных плоскостях. Может иметь несколько форм зубьев: прямые, косые и шевронные. Данный вид передач нашел свое применение в двигателях внутреннего сгорания, коробках передач подвижных составов, станков, буров. Он широко распространен в металлургии, машиностроении и других сферах промышленности.
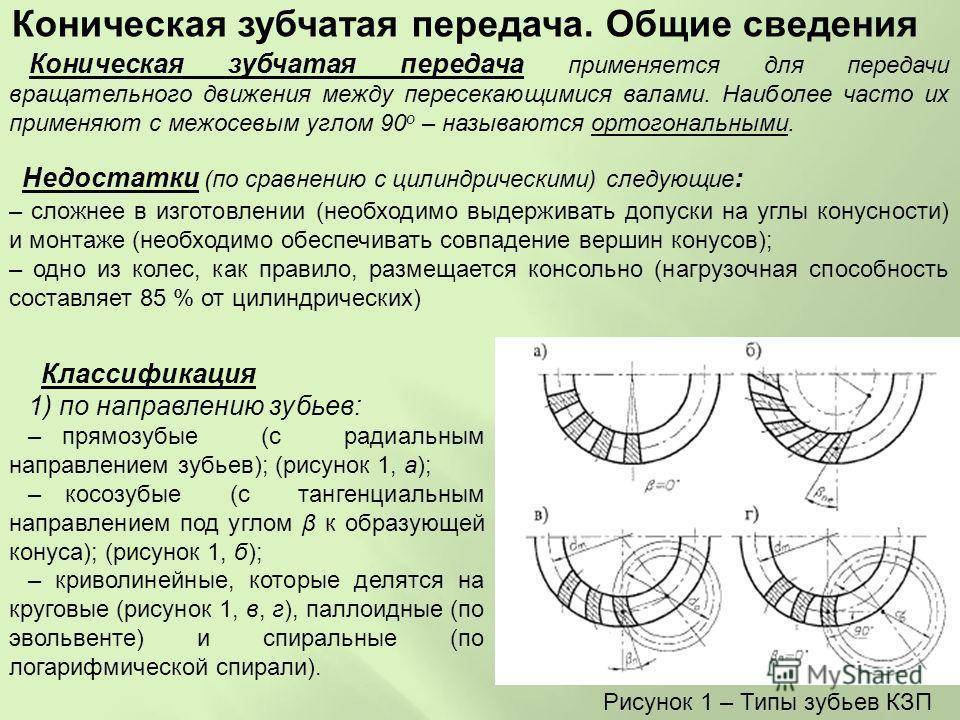
• Коническая. Получила свое название за счет необычной конструкции колесных пар. Имеет форму срезанного конуса, на котором нарезаны зубья. Величина профиля зубьев уменьшается от основания к вершине. Коническая зубчатая передача используется в сложных и комбинированных механизмах, для которых характерны частые изменения нагрузок и углов вращения. Примерами могут служить ведущие мосты автотранспорта, сельскохозяйственной техники или железнодорожных составов, приводы различных промышленных станков.
• Реечная. Используется для преобразования вращательного движения в поступательное, и наоборот. При этом одна из шестерен заменяется плоскостью с нарезанными зубьями. Реечная передача проста в производстве и установке, способна выдерживать значительные нагрузки. В основном она применяется в механизме станков, основанных на поступательном движении: прессы, транспортеры с попеременной подачей, рулевые механизмы управления в переднеприводных автомобилях.

Любой вид зубчатых передач отличается продолжительным эксплуатационным периодом и надежностью работы (при соблюдении определенного уровня нагрузки и своевременном обслуживании). Сравнительно небольшой механизм способен обеспечить высокий КПД, благодаря чему и применяется для широкого круга задач.